Изучив материал этой главы, ты будешь знать, что означают следующие термины и выражения:
многочлен, многочлен cтандартного вида, коэффициент многочлена, раскрытие скобок, разложение многочлена на множители, разность квадратов, квадрат разности, квадрат суммы, квадрат двучлена;
а также научишься:
- складывать и вычитать многочлены;
- умножать многочлен на одночлен;
- делить многочлен на одночлен;
- умножать многочлен на другой многочлен;
- раскладывать многочлены на множители путем вынесения общего множителя за скобки;
- пользоваться при раскрытии скобок и разложении многочленов на множители формулами разности квадратов, квадрата разности и квадрата суммы.
Что такое многочлен?
Подобные одночлены отличаются только числовым коэффициентом или же одинаковы, например,
3x2y и 4x2y; 2a и 2a; 5 и 12.
4a – 7a + 5a =
3a2 – 4a2 + 3a2 – 2 =
2x – 3y + 4x + 5y + 10 =
2ab2 – 7a2b + 5a2b – 2ab2 + 5 =
Приведенные выше выражения являются суммами одночленов. Сумму одночленов называют многочленом. Одночлены, при сложении которых получается многочлен, называются членами многочлена, а их коэффициенты – коэффициентами многочлена. Например, членами многочлена
являются 3x2, , y5 и –7, а коэффициентами 3, , 1 и –7.
Если среди членов многочлена есть подобные (то есть одночлены, отличающиеся только коэффициентами, или одинаковые одночлены), то их следует привести, как подобные слагаемые. Это ты и сделал в задаче 35. Чтобы избежать ошибок, подобные слагаемые следует подчеркнуть одинаковым способом. Например, многочлен
3ab2 – 7a2b + 5ab2 – a + 2a2b + 2
содержит две группы подобных. К одной группе принадлежат 3ab2 и 5ab2, к другой –7a2b и 2a2b. Приведя подобные слагаемые, получим:
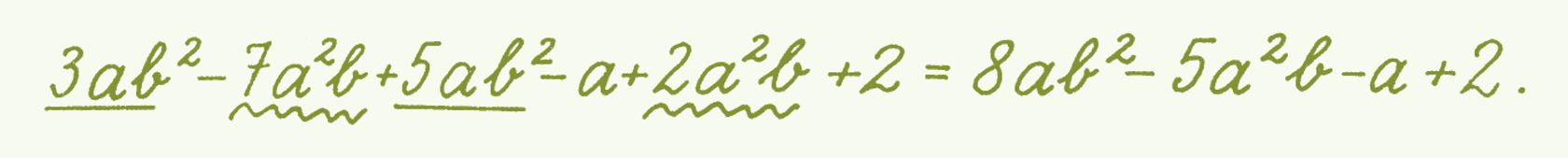 | ||||||||||||||
После приведения подобных члены многочлена обычно располагают так , чтобы на первом месте стоял тот из них, в котором сумма показателей степеней переменных является наибольшей. Если несколько членов имеют одинаковую наибольшую сумму показателей степеней, то их располагают произвольно. Остальные члены записывают в порядке убывания суммы показателей степеней переменных.
Одночлен записан в стандартном виде, если на первом месте стоит коэффициент, а произведения одинаковых переменных записаны в виде их степени (в алфавитном порядке оснований).
Если все члены многочлена записаны в стандартном виде и упорядочены описанным выше способом, то многочлен принимает стандартный вид. Полученный в последнем примере многочлен
8ab2 – 5a2b – a + 2
записан в стандартном виде. Наибольшая сумма показателей степеней его переменных a и b равна 3. В то же время многочлен
5x – 3x3 + 7x2 – 10x5 + 7
не записан в стандартном виде. Изменив порядок членов этого многочлена, мы можем записать его в стандартном виде. Получим:
5x – 3x3 + 7x2 – 10x5 + 7 = –10x5 – 3x3 + 7x2 + 5x + 7.
Многочлен, состоящий из двух неподобных членов, называется двучленом. Двучленами будут, например,
2x – 5, 3x2y + 7x, ax + b.
Многочлен, имеющий три неподобных друг другу члена, называется трехчленом. Таковы, к примеру,
2x3 – 3x + 5, a3 – ab + b2, x2 – 2y2 + z.
Упражнения A
 | ||||||||
- что такое многочлен, двучлен, трехчлен;
- что такое члены многочлена и коэффициенты многочлена;
- какой многочлен является записанным в стандартном виде.
5a – (–3a) + (–4a) – 8a =
–(–7x2) – 3x2 + (–x2) – (–5x2) =
6a – (–9) + 8a + (–9) – 7a =
–(–2y2) + 2 + (–y) – (–5) =
–6xy + (–5yx) + 8xy – (–2yx) =
Ответ: на эту поездку было израсходовано литров бензина.
Ответ: на полках магазина осталось кг муки.
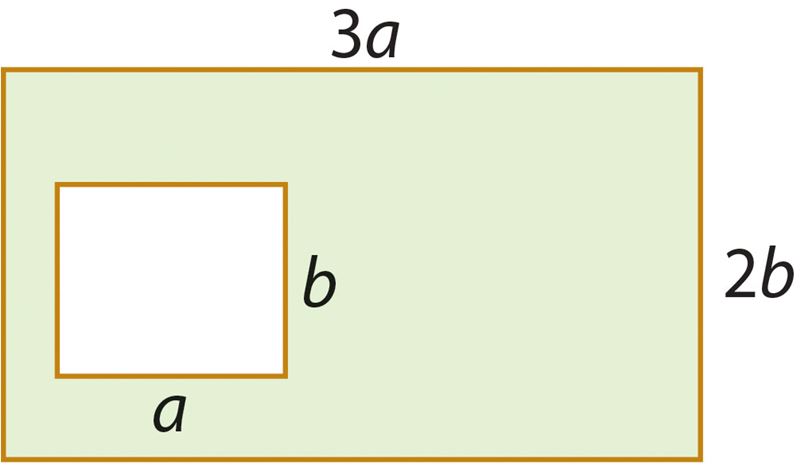
S =
Затем вычисли эту площадь, если a = 2,3 см и b = 3,9 см.
S = = (cм2).
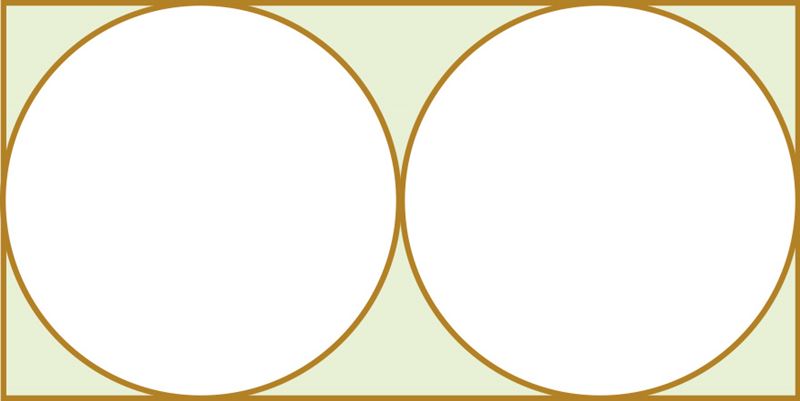 | ||||||
S =
Вычисли эту площадь, если r = 4,3 дм.
S = = (дм2).
Упражнения Б
 |
||||||||
Ответ: сумма этих одночленов есть и если x = –2, то ее значение равно .
–7a4 + (–5a2b) – (–6a4) + 3ba2 – 6ab – (–4ab2) =
5abc – (–7ab) + (–6) – 9ba + (–ac) + (–5acb) =
4(a + b) – 9(a – b) + 3(a + b) + 4(a – b) + 7(a + b) =
an + (–7am) – (–3an) – a2m + (–4an) – a2m =
- сколько проволоки пошло на изготовление каркасов;
Ответ: на изготовление каркасов пошло см проволоки. - какова общая площадь бумаги, израсходованной на изготовление кубов;
Ответ: на изготовление кубов было израсходовано cм2 бумаги. - каков суммарный объем этих кубов.
Ответ: сумма объемов кубов равна cм3.
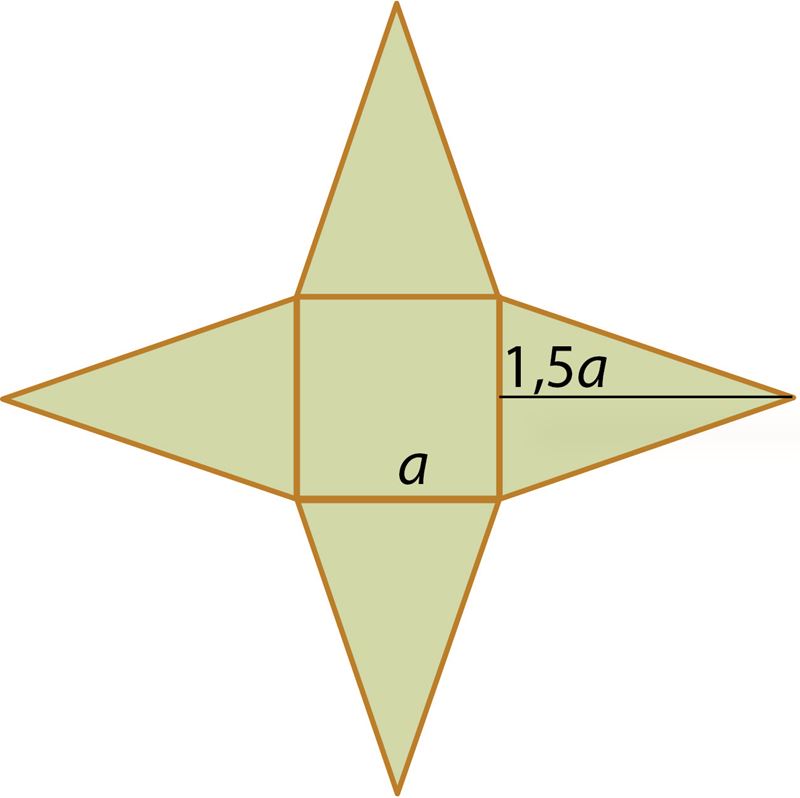
Ответ: площадь фигуры составляет единиц площади. Площадь квадрата составляет % от суммы площадей всех треугольников.
- двузначное натуральное число, в котором a десятков и b единиц;
- трехзначное натуральное число, в котором x сотен, y десятков и z единиц;
- двузначное натуральное число, в котором a единиц, a десятков в 3 раза больше.
Ответ: это число равно .
Ответ: это число равно .
Ответ: в стае было гусей.
Ответ: площадь прямоугольника %.
