При изучении этого раздела сначала нужно вспомнить изученное в предыдущих классах. Для этого реши приведенные здесь задачи.
Обоснуй по рисунку, что
- ∆ABC = ∆EDC;
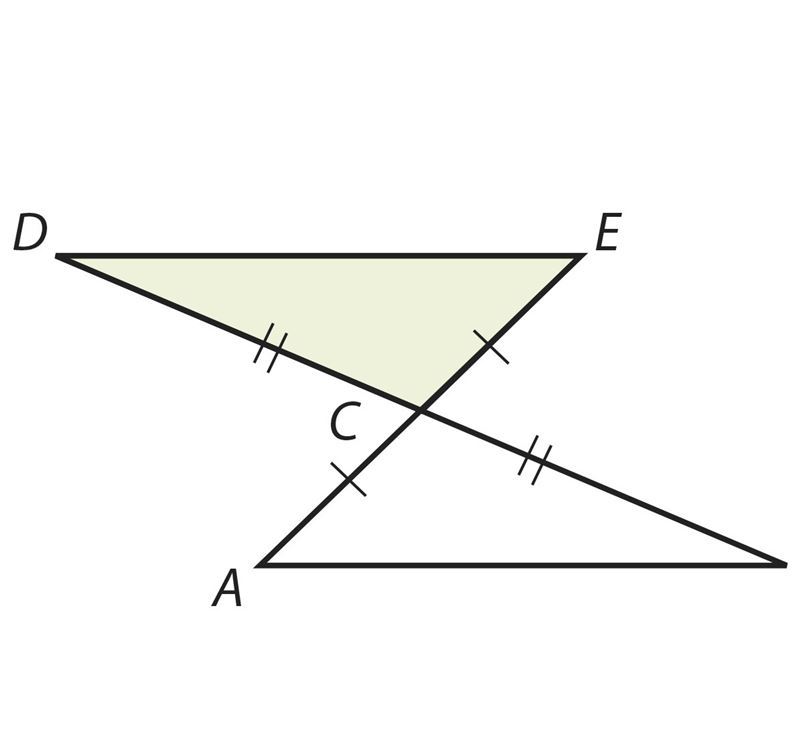
- ∆MON = ∆LOK;
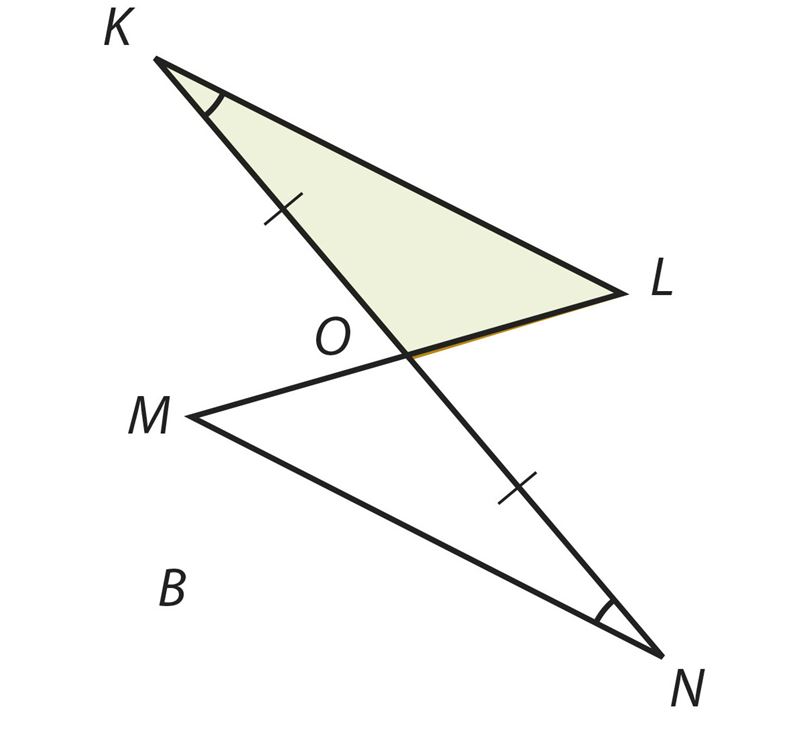
- ∆PQT = ∆RQT.
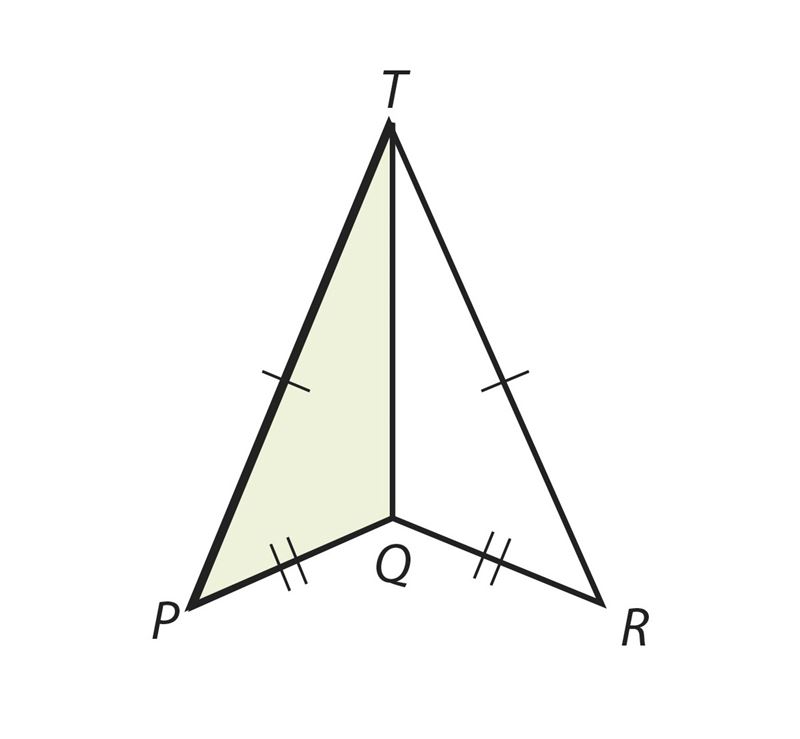
Можно ли по рисунку утверждать, что AB || CD.
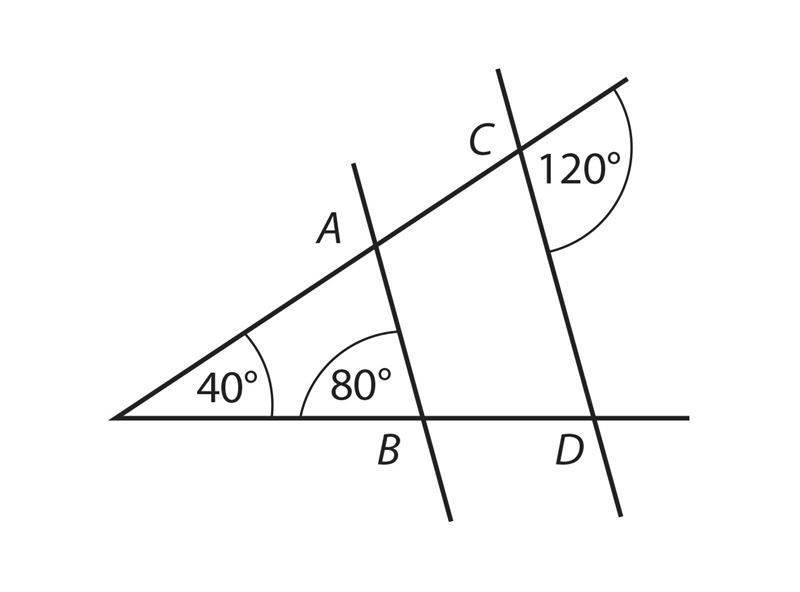
Ответ:
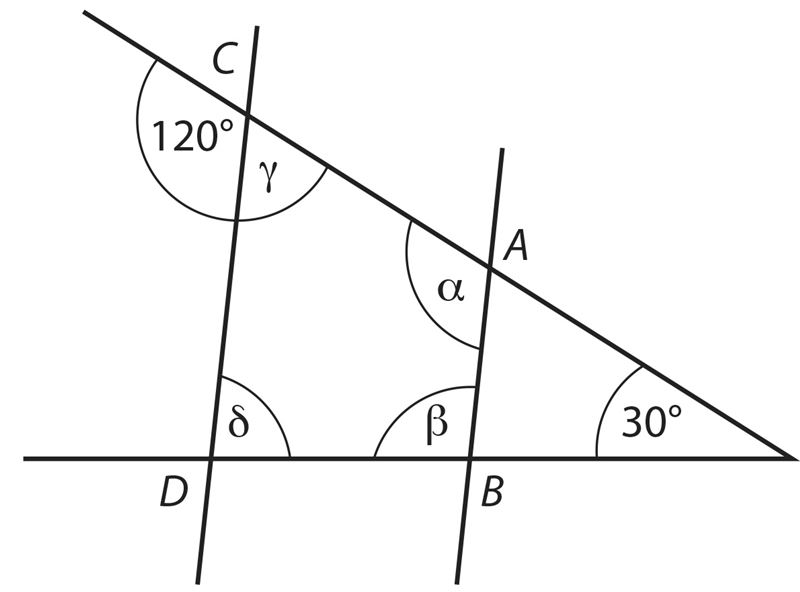
α = ˚
β = ˚
γ = ˚
δ = ˚
В предыдущем параграфе (§ 5.3) мы выяснили, что при пересечении сторон угла параллельными прямыми образуются треугольники с пропорциональными сторонами.

Два треугольника называются подобными, если три стороны одного треугольника пропорциональны трем сторонам другого треугольника.
Это предложение является определением подобия треугольников.

Учитывая это определение, мы можем следствие из теоремы Фалеса предыдущего параграфа сформулировать по-другому:
при пересечении сторон угла параллельными прямыми образуются подобные треугольники.
 |
||||||||||
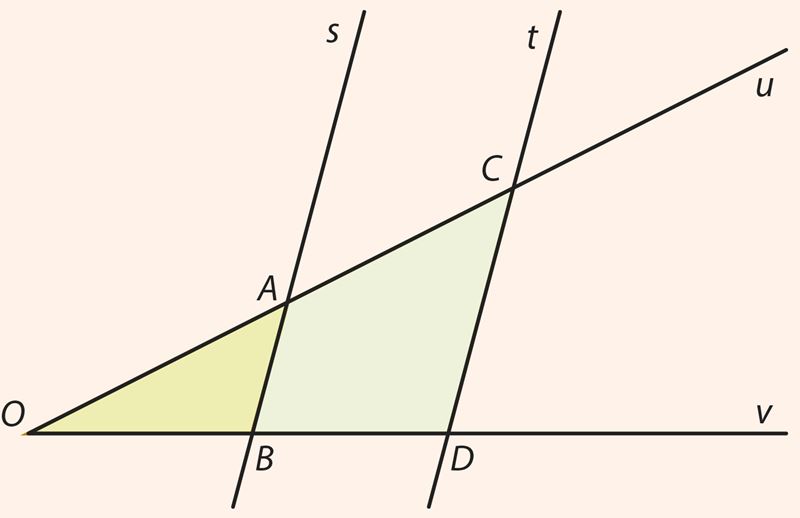
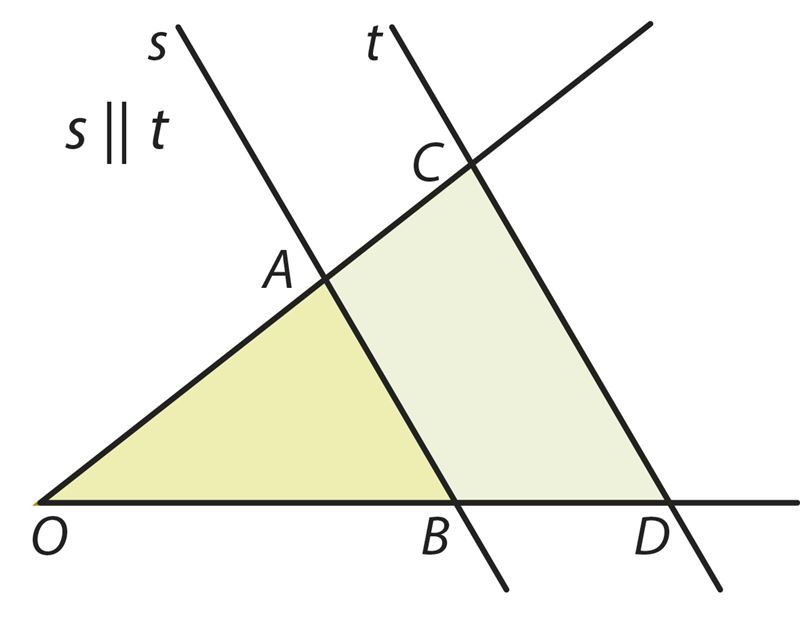
Подобие треугольников обозначается так: ∆OAB ∼ ∆OCD. При этом треугольники обозначают так, что их соответствующие вершины располагаются в одном и том же порядке. При такой записи легко определить соответствующие друг другу стороны треугольников: OA → OC, OB → OD, AB → CD.
Подобные треугольники имеют «одинаковую форму», но разную величину. Это значит, что если два треугольника подобны, то один из них является увеличенной или уменьшенной (в частном случае – равной) копией другого.
 |
||||||
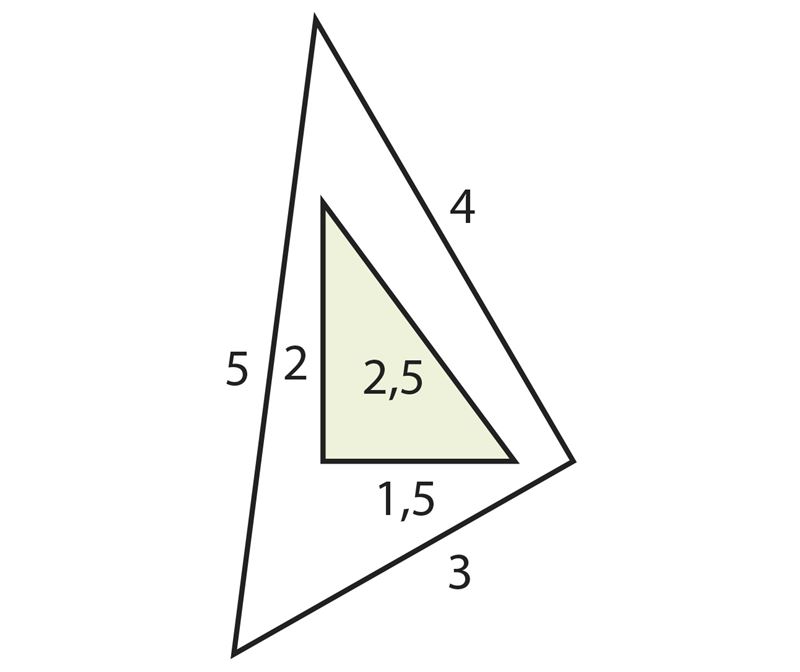
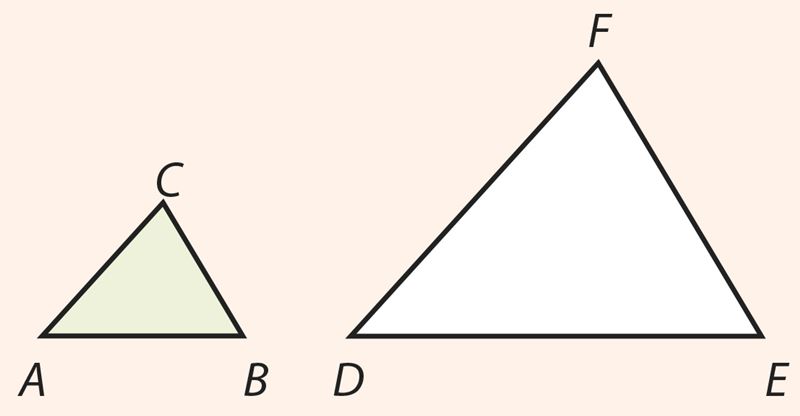
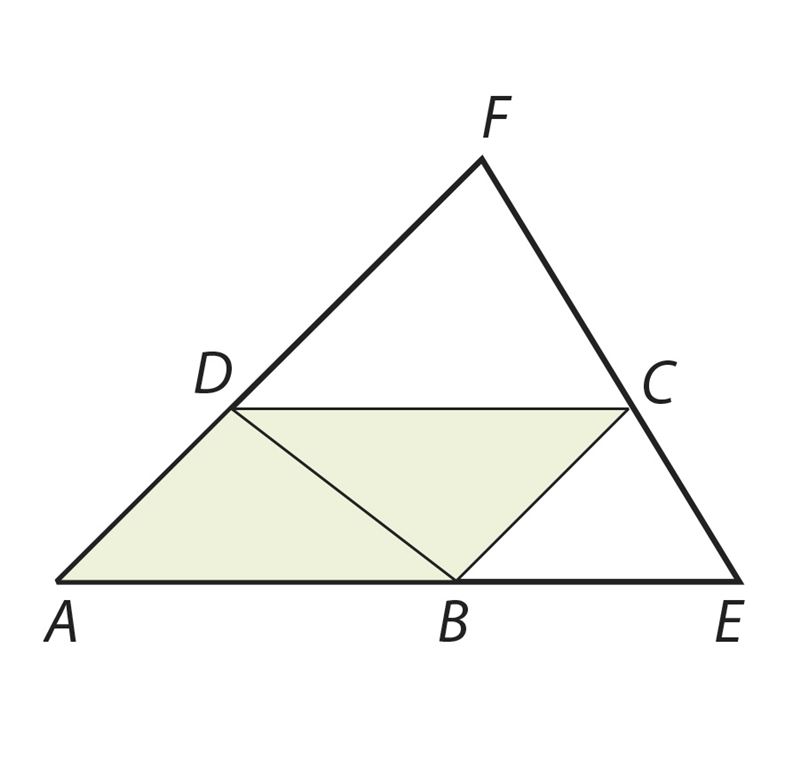
Например, треугольники АВС и DEF на рисунке подобны, так как их стороны пропорциональны:
.
Проверь это с помощью измерений.
Положительное число, равное отношению соответствующих сторон подобных треугольников, называется коэффициентом подобия. В примере коэффициентом подобия является число 2. Разумеется, коэффициент подобия зависит от того, стороны какого треугольника записаны в числителях и стороны какого – в знаменателях отношений.
 |
||||||||
При продолжении боковых сторон трапеции ABCD до их пересечения в точке Е образуются два треугольника: ∆ABE и ∆DCE.
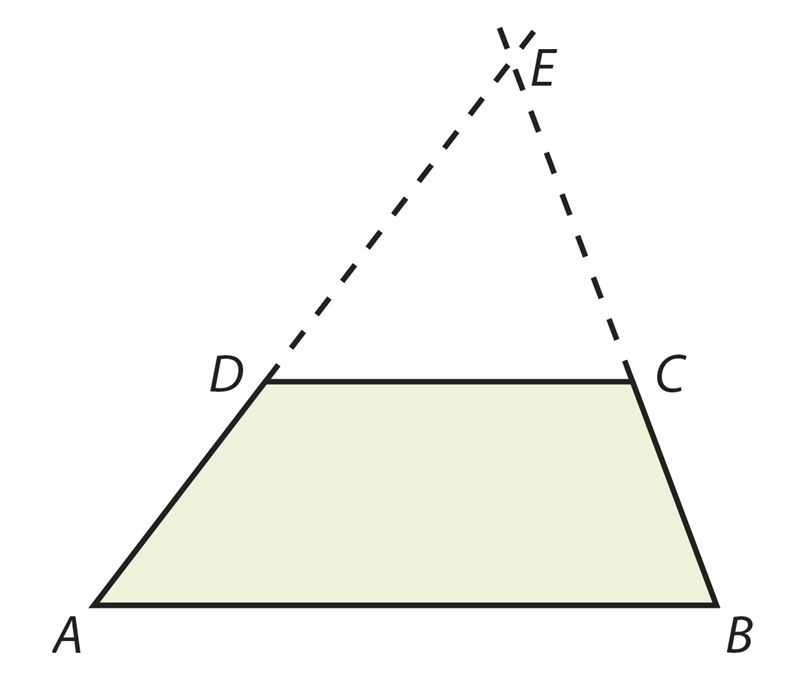
Эти треугольники подобны в силу параллельности оснований трапеции и теоремы Фалеса (§ 5.3). Запиши отношения соответствующих сторон этих треугольников.
Упражнения A
 |
||||||||
Ответ: другие стороны второго участка равны м и м, а его периметр равен м.
Ответ: стороны участка на местности имеют длину м и м. Масштаб плана есть .
Упражнения Б
 |
||||||||
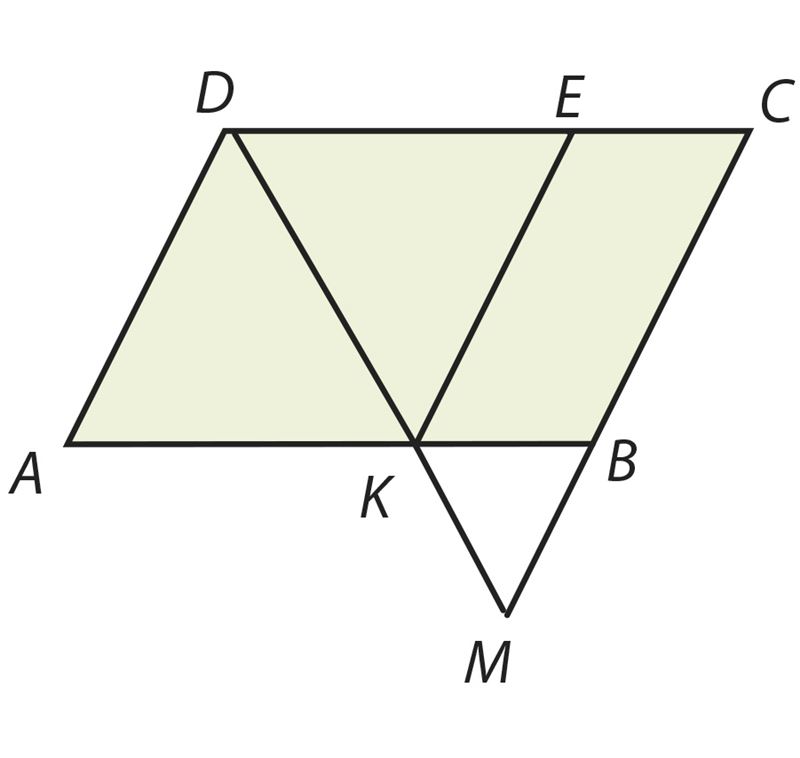
Ответ: стороны треугольника равны см, см и см.
Ответ: для пересечения одну боковую сторону нужно удлинить на см, а другую сторону – на см.
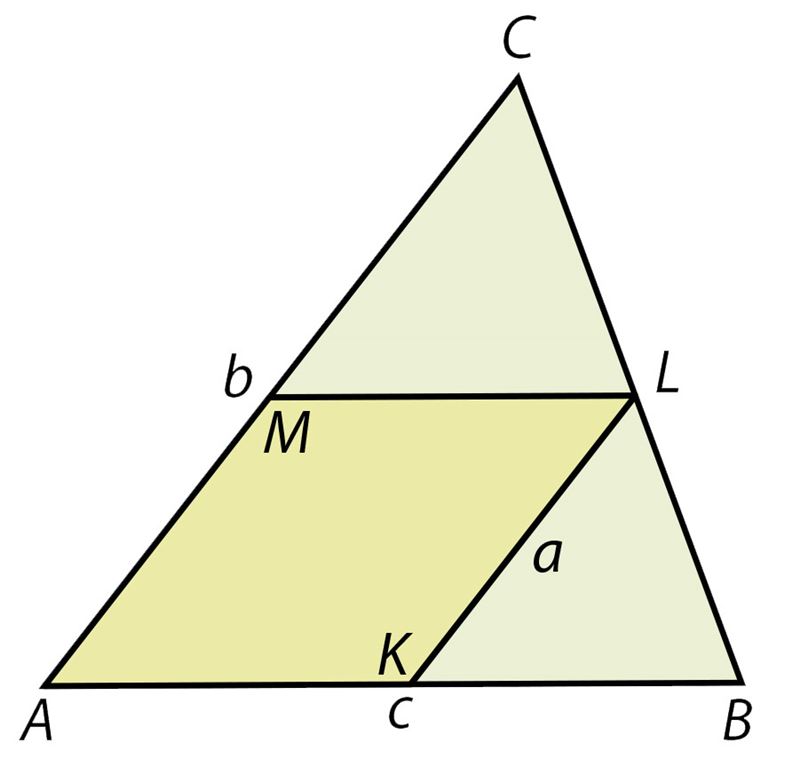
Ответ: a =
Вычисли сторону ромба, если с = 12 см и b = 18 см.
a = = (см).
- AP · PQ = AR · BP
- AC · BP = AB · PQ
Ответ: остальные стороны второго треугольника равны см и см.
Ответ: стороны второго треугольника равны