Покажем, что любому линейному уравнению с двумя неизвестными можно дать графическое истолкование. Рассмотрим, например, уравнение 4x – 2y = 3. Выразим в нем неизвестное y через x:
–2y = 3 – 4x, откуда
y = 2x – 1,5.
Мы видим, что наше уравнение представляет собой линейную зависимость y = 2x – 1,5, т. е. линейную функцию, изученную в 7 классе. Но графиком этой зависимости является прямая. Координаты каждой точки этой прямой удовлетворяют данному уравнению.
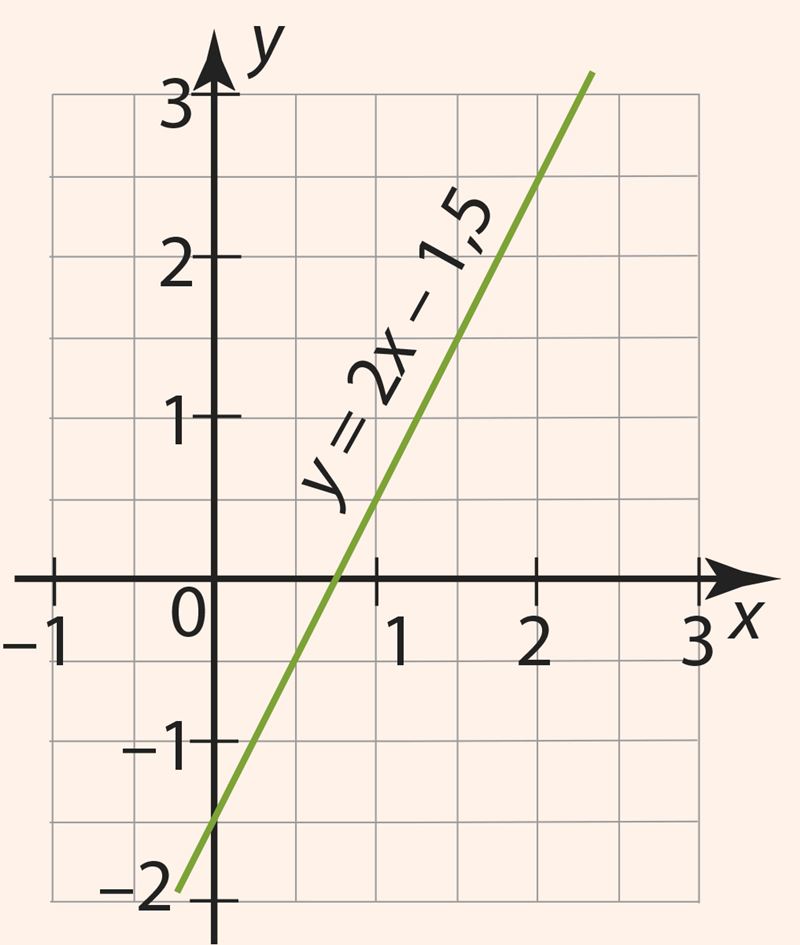 |
||||||
Так же можно рассуждать в случае любого линейного уравнения с двумя неизвестными. Отсюда мы можем сделать вывод:

графиком линейного уравнения с двумя неизвестными является прямая линия.
Координаты каждой точки этой прямой удовлетворяют данному уравнению и каждое решение уравнения изображается точкой, расположенной на этой прямой.
Так как графическим изображением линейного уравнения ax + by = c с двумя неизвестными является прямая, то это уравнение называют уравнением прямой. Для краткости вместо выражения «прямая, уравнением которой является ax + by = c» обычно употребляют выражение «прямая ax + by = c».
Чтобы начертить прямую, нужно знать координаты двух различных точек этой прямой. Удобно брать точки пересечения этой прямой с осями координат, поскольку эти точки легко найти: одна из координат точки, расположенной на координатной оси, всегда равна 0.
 |
||||||||
Начертим прямую 3x – 2y = 6.
Чтобы найти точки пересечения искомой прямой с осями координат, удобно составить таблицу. Сначала возьмем число 0 в качестве значения x и вычислим соответствующее значение y, затем, наоборот, возьмем y = 0 и вычислим из уравнения значение x.
Для данного примера получим:
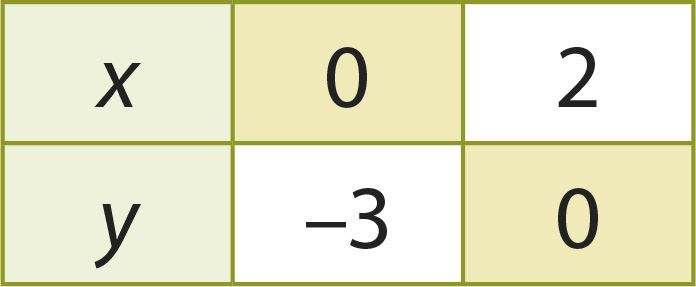 | |||||
откуда следует, что прямая 3x – 2y = 6 пересекает координатные оси в точках A(0; –3) и B(2; 0). Через эти две точки проведем искомую прямую.
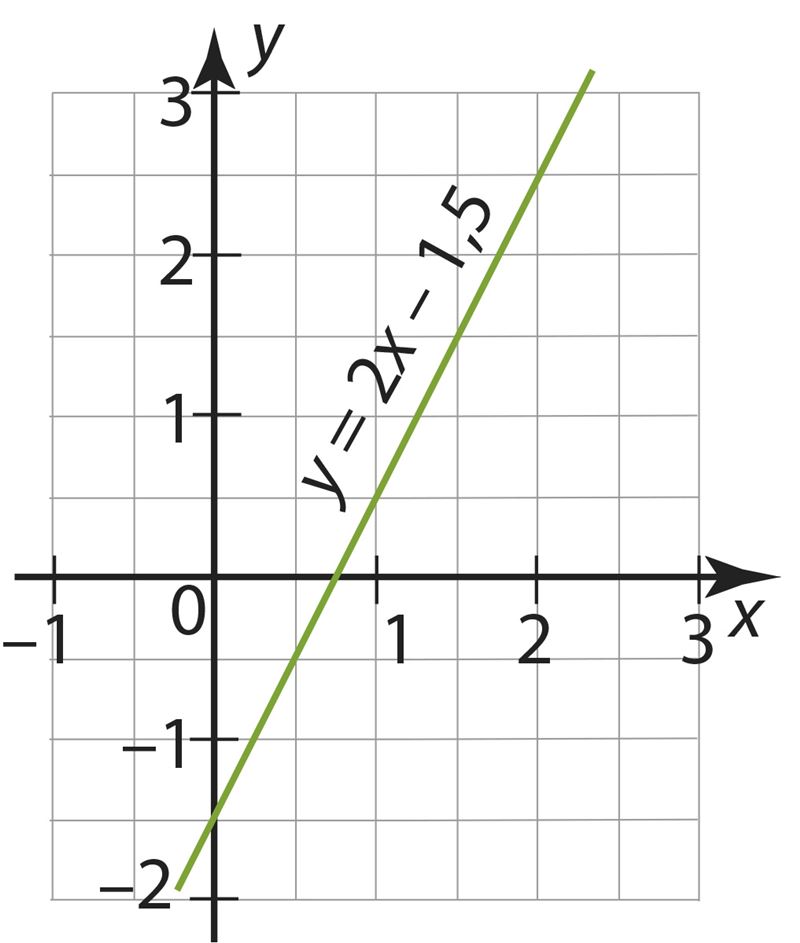
Неизвестные значения найдем, решив уравнения 3 · 0 – 2y = 6 и 3x – 2 · 0 = 6.
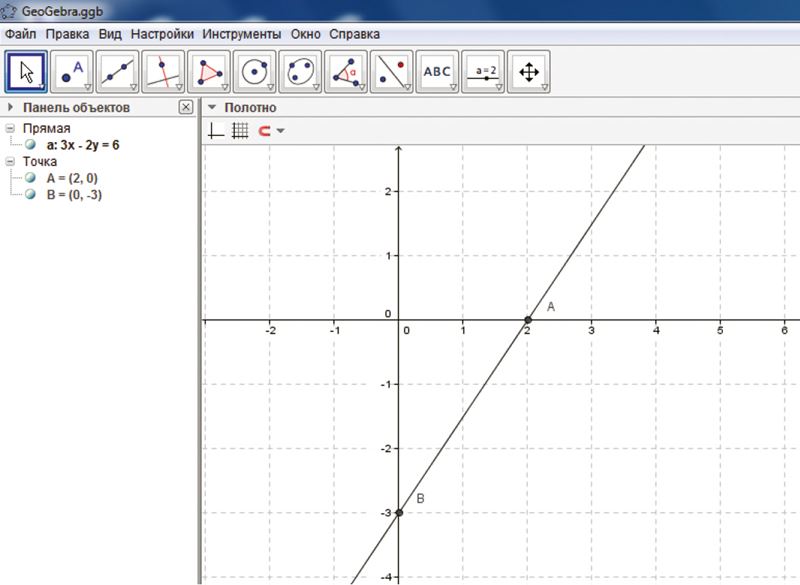
Линейное уравнение с двумя неизвестными можно изобразить графически с помощью программы GeoGebra. Чтобы ввести уравнение, запишем его в окне Ввод (например, 3x-2y=6, без пробелов!) и нажмем ENTER. Введенное уравнение вместе с обозначением мы видим также в окне Панель объектов (программа может сама привести уравнение к стандартному виду).
Убедимся, что прямая пересекает координатные оси в точках A(0; –3) и B(2; 0).
Для этого выберем Пересечение двух объектов. Кнопку „Пересечение двух объектов” найдешь, щелкнув мышью в треугольник в нижнем правом углу кнопки („Точка”). Если теперь щелкнуть мышью на прямой и затем на оси Ох, то мы увидим точку пересечения как на графике, так и в алгебраическом описании на панели объектов. Аналогично найдем точку пересечения прямой с осью Оу.
 „Пересечение двух объектов” |
||||||||||||||||
 „Точка” |
||||||||||||||||
При использовании строки ввода программы GeoGebra нужно учитывать следующее.
- Название файла в формате .ggb нужно писать латиницей.
- В десятичных дробях вместо запятой надо ставить точку (как в англоязычных странах).
- Знаком умножения является звездочка *, а знаком деления – наклонная черта /.
- Выражение, содержащее дробь, можно ввести как частное. При этом не забывай ставить скобки. Уравнение можно ввести так: (x+2)/4=(y-1)/3.
- В качестве переменных или неизвестных программа использует только соответствующие координатным осям х и у. Если уравнение содержит другие переменные, их нужно переобозначить на х и/или у.
Упражнения A
 |
||||||||
- каким свойством должны обладать координаты каждой точки прямой, чтобы эта прямая была графиком уравнения, например, уравнения 3x – 5y = 2;
- как найти точки пересечения этой прямой с осями координат.
- построй с помощью программы GeoGebra прямую 3x – 5y = 2, найди точки пересечения этой прямой с координатными осями.
aбсцисса – координата x,
oрдината – координата y
Ответ: ордината этой точки равна .
Ответ: абсцисса этой точки равна .
- (1; –1)
- (0; –4)
- (1,4; 0)
- (2,7; 1,5)
2x – 5y = 6
x | 0 | |||
y | 0 |
–3x + 2y = 8
x | 0 | |||
y | 0 |
3x + 5y = –15
x | 0 | |||
y | 0 |
Ответ: решениями этого уравнения будут, например, , , и .
Упражнения Б
 |
||||||||
Ответ: уравнением подходящей прямой является, например, .
14x – 17y = 238
x | 0 | |||
y | 0 |
0,23x + 1,15y = –4,6
x | 0 | |||
y | 0 |
0 · x + 2y = –8 | |
0 · x – 2y = 6 | |
0 · x + 3y = –9 | |
x + 0 · y = 7 | |
3x + 0 · y = 12 | |
4x + 0 · y = –6 |
Ответ: b =
Ответ: a =
Ответ: Денис купил , или карандашей.
