Умножение двучленов

Выясним, чему равно произведение двух двучленов a + b и c + d, т. е.

(a + b)(c + d).

Если значения переменных a, b, c и d положительны, то данное про­изведение можно рассматривать как площадь прямоугольника, у ко­то­рого одна сторона равна a + b, а другая сторона c + d (см. рисунок). Этот прямо­угольник разбивается на четыре прямоугольника, площади которых ac, ad, bc и bd.

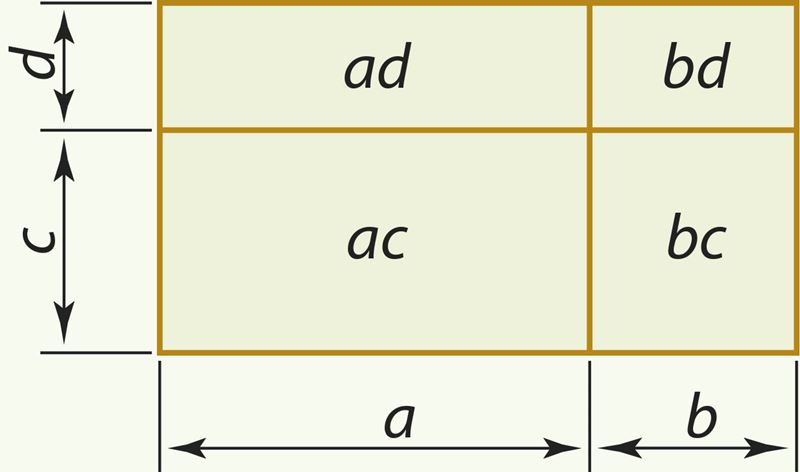
Следовательно,

(a + b)(c + d) = ac + ad + bc + bd.

Тот же результат можно получить, не привлекая геометрической иллюстрации и считая переменные a, b, c и d произвольными числами. В самом деле, применим распределительный закон умножения, считая двучлен a + b суммой, которую нужно умножить на число c + d. Получим:

(a + b)(c + d) = a(c + d) + b(c + d).

Применив еще раз тот же закон к умножению на сумму c + d, получим:

(a + b)(c + d) = ac + ad + bc + bd.

Проведенные рассуждения можно изобразить схемой:

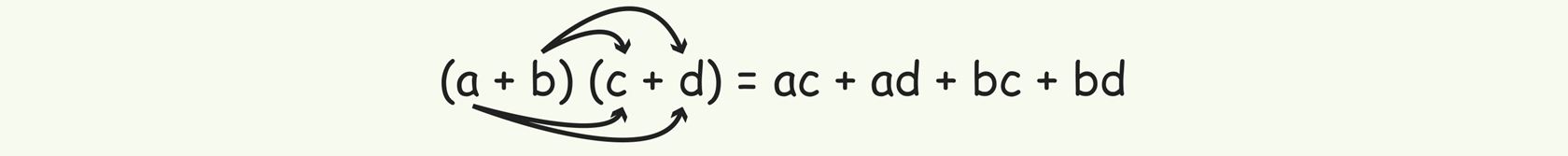
Чтобы умножить двучлен на двучлен, нужно каждый член одного двучлена умножить на каждый член другого двучлена и полученные произведения сложить.

Если при умножении двучленов в полученном многочлене обра­зуются подобные слагаемые, то нужно их привести.

(2x + 3)(4x – 2) =
=​ 2x · 4x + 2x · (–2)  +  3 · 4x + 3 · (–2) =
=​ 8x2 – 4x + 12x – 6 =
=​ 8x2 + 8x – 6

При письменных вычислениях подчеркнутое выражение обычно не записывают. В этом случае запись умножения становится короче.

(4x – 5y)(3x + 2y) =
=​ 12x2 + 8xy – 15xy – 10y2 =
=​ 12x2 – 7xy – 10y2

Объясни каждый шаг выполненного в этом примере умножения.

Правило умножения двучленов часто приходится использовать при упрощении более сложных выражений.

(6a – 3)(2a + 3) – (3a – 4)(2a + 1) =
=​ 12a2 + 18a – 6a – 9 – (6a2 + 3a – 8a – 4) =
=​ 12a2 + 12a – 9 – 6a2 + 5a + 4 =
=​ 6a2 + 17a – 5.

Объясни каждый шаг выполненного умножения. Почему во второй строчке один из многочленов заключен в скобки?

More like this
More options

Упражнения A
  1. Проверь, помнишь ли ты правило умножения двучленов.
  2. На примере произведения (3a – 5)(2a + 1) объясни, как вы­­полняется умножение двучленов.

(x + y)(a + b) = 

(m – n)(c + 4) = 

(a – x)(b – y) = 

(3 + x)(–v + y) = 

(u + v)(a – c) = 

(–s – t)(p – r) = 

(a + b)(m + 1) = 

(8 – c)(–x + y) = 

(t – u)(x – 2) = 

(–f + g)(b + c) = 

(y – x)(a + z) = 

(1 + z)(d + x) = 

(3x – 1)(2x + 4) =  = 

(a + 5)(3a + 2) =  = 

(7 – 4y)(1 – 2z) =  = 

(–b + 6a)(5 – a) =  = 

(5a + b)(c + 2) =  = 

(4m + n)(n – 4m) =  = 

(8x – 2y)(2x + 3y) =  = 

(u + 4v)(u – 4v) =  = 

(6x + y)(6x + y) =  = 

(c – 11)(4c + 2) =  = 

(–5 + z)(z + 5) =  = 

(8a + b)(8b – a) =  = 

(ac + 1)(ac – 3) =  = 

(x – 8)(2x – 3) =  = 

(4 – xy)(4 + xy) =  = 

(c + ab)(b – ac) =  = 

(a + b)(a – b) – a(a +1) =  = 

(3m – 2n)(m + n) + m(n – 3m) =  = 

(4a + 3)(2a – 1) – 2a(a + 1) =  = 

(c – d)(c – d) – (c + d)(c + d) =  = 

(5y + x)(2y – 3x) + x(2x + 13y) =  = 

s(2s + 3t) – (s – 2t)(2s – t) =  = 

(4a – 1)(a + 2) – 4a(a + 1) =  = 

Если a = –1,7, то значение выражения равно

 = .

(c – 3)(5 + 2c) + 3(c + 5) =  = 

Если c = 1,5, то значение выражения равно

 = .

(a + b)(a + b) – (a2 + b2) =  = 

Если a = –0,5 и b = 1,97, то значение выражения равно

 = .

(x + 5)(x – 2) – x(x + 7) = 2
x = 

y(10y + 9) = 7 + (5y – 1)(2y + 3)
y = 

(2z – 3)(2 + z) = z(2z – 5)
z = 

(n – 1)(n + 3) – (n + 5)(n – 2) = 5
n = 

3t2 = 8 + (3t + 2)(t – 1)
t = 

Ответ: эти числа (в порядке возрастания) есть  , , , .

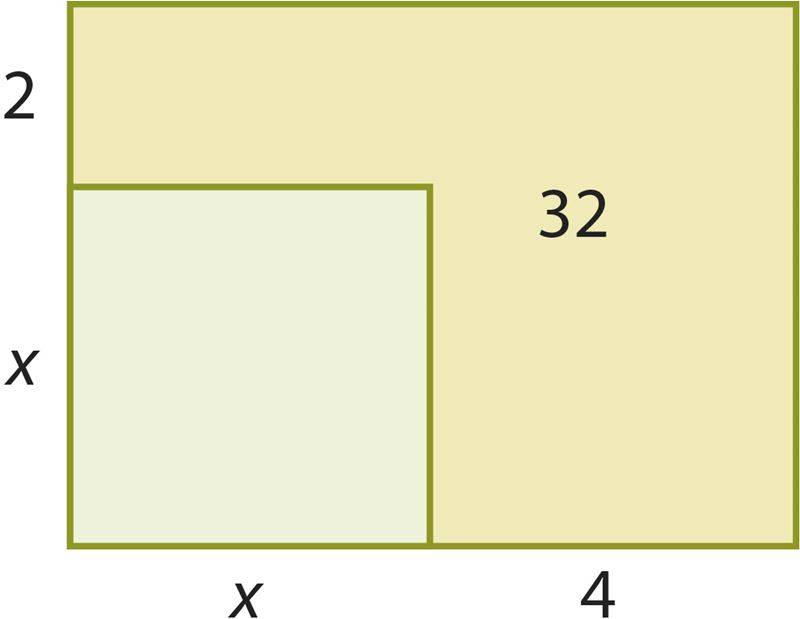
Ответ: сторона квадрата равна  м.

1)

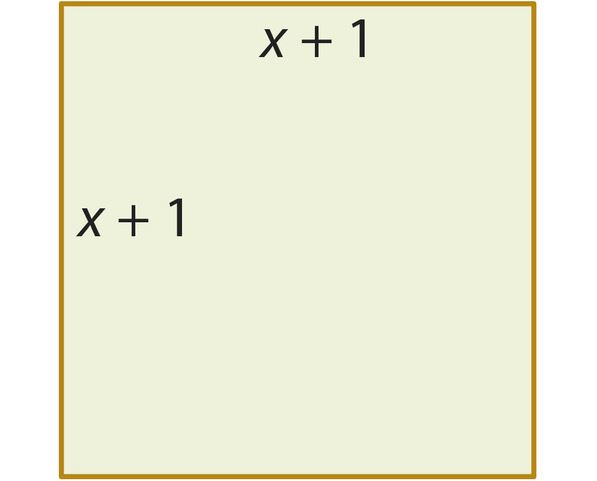
S =  = 

2)

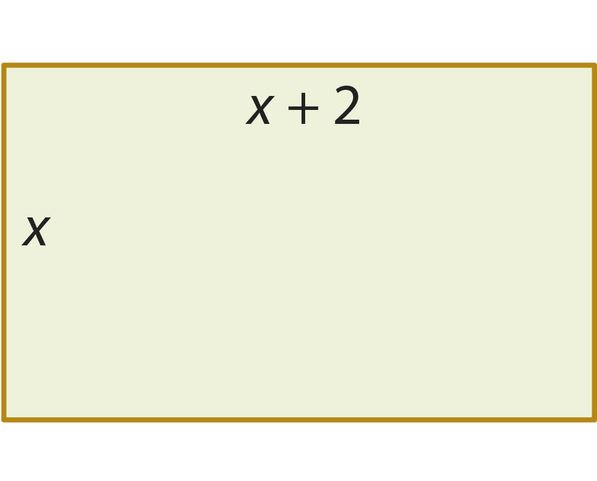
S =  = 

Ответ: бóльшую площадь имеет  прямоугольник.

Попробуй решить эту задачу в уме, затем проверь свой ответ, составив и решив уравнение.

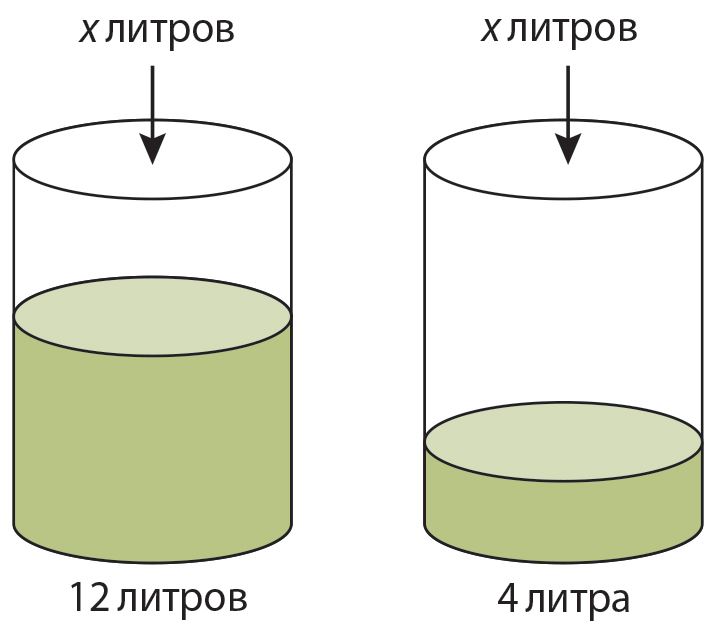
Ответ в оба сосуда долили по  литра воды.

Совет
При устном решении предположи сначала, что долили, к примеру, 1 л воды, затем 2 л и т. д. Такой метод решения задачи называется методом проб. Одним из способов решения задач является также составление и решение уравнения.
More like this
More options

Упражнения Б

(x3 – x2)(x3 + x2) = 

(5x4 – 3x)(4x3 + x) = 

(1,8z5 – z3)(2z3 – 3z) = 

(a2b – b2)(ab2 + a) = 

(x3 – 4z)(–x3 – z) = 

(x2 + 1)(xn – 1) = 

(an – bm)(an + bm) = 

(x2 – 2)(xn–2 + 1) = 

(ym+1 – ym–2)(y + y2) = 

(b2n – bn)(b3n + b2n) = 

(5x3 – 2)(3x + 1) – 1,5x(10x3 – 6) – 3(x + 1) = 

(3x – 1)(x + 1) + (2x – 1)(x – 1) – (3x + 5)(x – 2) = 

4x2(x2 – 3x + 1) – (4x2 – 3)(x2 – x) + 7x(1 – x) = 

(5a – 2b)(a + b) – 3a(a – 4b) + 2b(b – 7a) = 

a(a + b + c) – (a + b)(a – c) – b(a + c) = 

(x – a)(x + b) – x(a + b) + ab = x(x – 2a)

m2(m – 2) – m(m2 – 4) = 2m(2 – m)

x(x – y – z) + (y + z)(x + z) – x(x + z) = z(z + y – x)

Подсказка
Четыре последовательных целых числа – это n, n + 1, n + 2 и n + 3. Этому условию соответствуют и другие обозначения – например, а – 2, а – 1, а и а + 1

x2 – (x – y)(x – y) +2(xy – y2) = 

Если x = 96 и y = 11, то значение выражения равно

 = .

(a + 2y)(2a – y) – a(y + 2a) = 

Если a = –1,6 и y = 0,4, то значение выражения равно

 = .

(y – 1)(y – 2) + (y – 2)(y – 3) = 2(y2 – 7y + 12) + 2
y = 

(5 – x)(5 + x) – (x + 4)(x – 1) = 5 – 2x2
x = 

3(t2 – t + 1) – (t + 2)(3t – 4) = t – 4
t = 

Ответ: сторона квадрата равна  cм.

(a + b)c +(a + b)d = 

(m – 3)x +(m – 3)y = 

(a2 + b) + (a2 + b)c = 

ac + ad + bc + bd = 

ax – ay + bx – by = 

ax – 2a – bx + 2b = 

More like this
More options