Произведение суммы и разности двух одночленов

(m + n)(m – n) = =

(x – y)(x + y) = =

(a + 2)(a – 2) = =

Объясни, чем отличаются друг от друга перемножаемые двучлены. Выполнив умножение, сделай вывод и сформулируй обнаруженную закономерность.

(2a – b)(2a + b) = =

(a – 3b)(a + 3b) = =

(2 – 5x)(2 + 5x) = =

Объясни, чем отличаются друг от друга перемножаемые двучлены. Выполнив умножение, сделай вывод и сформулируй обнаруженную закономерность.

(2x – 3y)(2x + 3y) = =

(x² + 2y)(x² – 2y) = =

(x² – 3)(x² + 3) = =

Объясни, чем отличаются друг от друга перемножаемые двучлены. Выполнив умножение, сделай вывод и сформулируй обнаруженную закономерность.

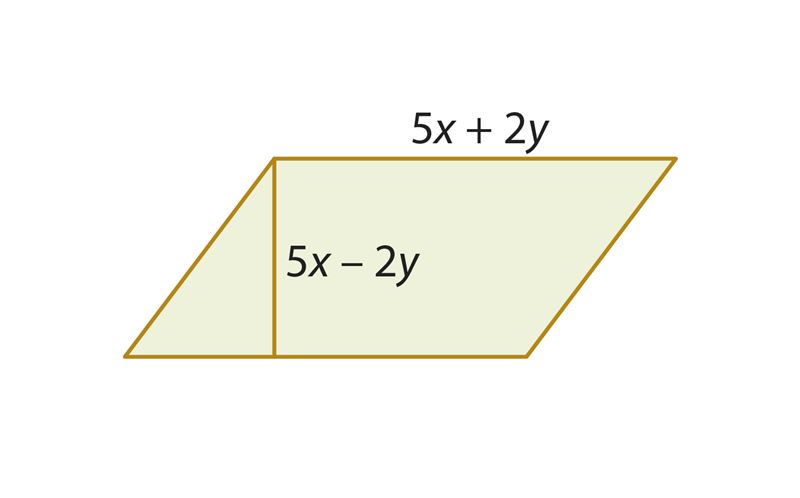
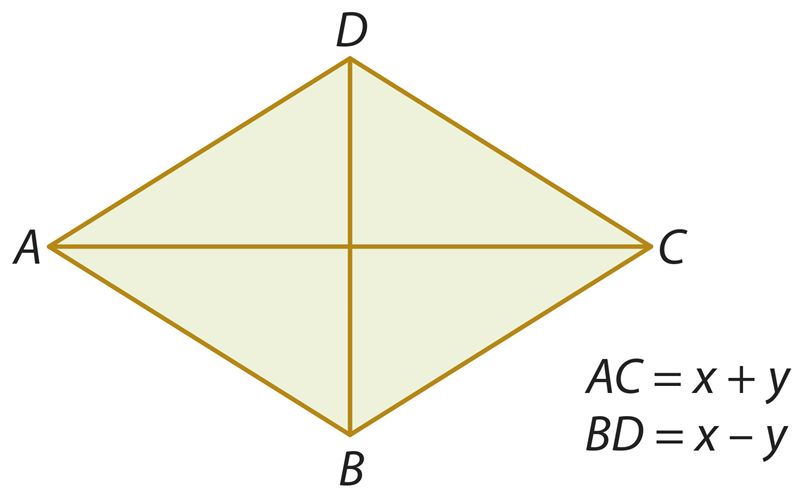
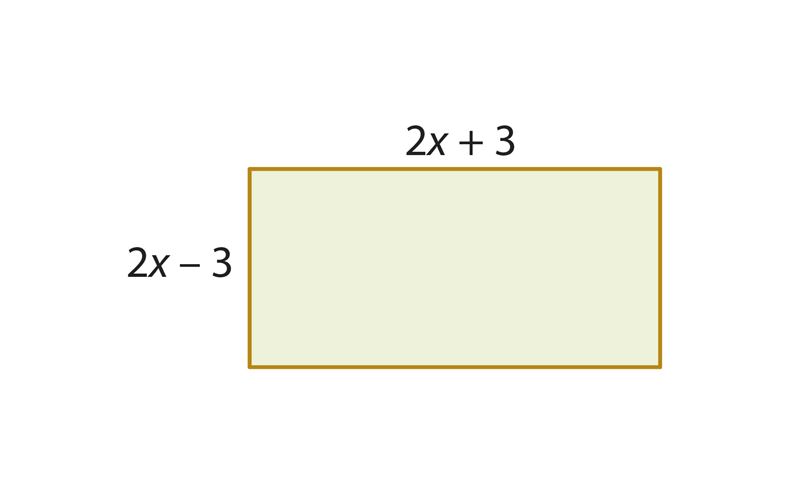В рассмотренной задаче ты умножал такие двучлены, один из которых является суммой одночленов, а другой – разностью тех же одночленов. В многочлене, полученном умножением суммы одночленов на их разность, два члена всегда взаимно уничтожаются и в результате остается разность квадратов этих одночленов (в том же порядке, что и в исходной разности). Запишем это в виде формулы:

(a + b)(a – b) = a² – b²

Полученная формула называется формулой разности квадратов.

Произведение суммы двух одночленов на их разность равно разности квадратов этих одночленов.

Это правило позволяет упрощать многие вычисления и его нужно запомнить.

(2a – 3b²)(2a + 3b²) = (2a)² – (3b²)² = 4a² – 9b⁴
(5x² + 2)(5x² – 2) = 25x⁴ – 4

Seotud sisu

Упражнения A

186. Произведение суммы двух одночленов на их разность

Внимательно прочитай текст параграфа и разбери примеры. Запомнил ли ты формулу произведения суммы двух одночленов на их разность (формулу разности квадратов) и можешь ли ты сформулировать соответствующее правило?

(☐ + △)(☐ – △) = (☐)² – (△)²

(a + 3)(a – 3) =

(b + 5)(b – 5) =

(c – 8)(c + 8) =

(a – 4)(a + 4) =

(b + 1)(b – 1) =

(c + 0,5)(c – 0,5) =

(x – 0,7)(x + 0,7) =

(0,4 + u)(0,4 – u) =

(0,9 – y)(y + 0,9) =

(0,1 + a)(a – 0,1) =

(4x + 7)(4x – 7) =

(2a – 5b)(2a + 5b) =

(6c + 1)(6c – 1) =

(3m – 9n)(3m + 9n) =

(10y – 2z)(10y + 2z) =

(6y + 11)(6y – 11) =

(5u – 3v)(5u + 3v) =

(12t – 8s)(12t + 8s) =

(4r + 7p)(7p – 4r) =

(25 – 10a)(25 + 10a) =

(ab – 1)(ab + 1) =

(4 + xy)(4 – xy) =

(2cd + 3)(2cd – 3) =

(x² – y)(x² + y) =

(m² + n²)(m² – n²) =

(2a² + 3)(2a² – 3) =

(5x² – 4)(5x² + 4) =

(st – 2v)(st + 2v) =

(1,5n + 6)(1,5n – 6) =

(0,3m – 8p)(0,3m + 8p) =

(a – b)(a + b) – b(a – b) = = =

(3x + 4)(3x – 4) – 2(x² – 8) = = =

(m – n)(m + 2n) – (m – n)(m + n) = = =

(4x – 2y)(x + 2y) + (2y + x)(2y – x) = = =

(c – d)(c + d) – (c + d)(c – d) = = =

(5a – c)(5a + c) + (c + 3a)(c – 3a) = = =

(4y – 1)(4y + 1) + 7(1 – 2y²) = =

Если y = –10, то значение выражения равно

=

a(a + 4) – (a + 2)(a – 2) = =

Если a = –1,25, то значение выражения равно

=

S =

Если x = 6, то

S = = (дм²).

S =

Если x = 6 и y = 4, то

S = = (дм²).

S =

Если x = 6 и y = 4, то

S = = (дм²).

Seotud sisu

Упражнения Б

(2y³ + 15)(2y³ – 15) =

(0,1uv³ – x)(x + 0,1uv³) =

(0,2a² + b²)(0,2a² – b²) =

(a²b – mn²)(a²b + mn²) =

$(\frac{2}{7} y^{3} + \frac{5}{6} t) (\frac{2}{7} y^{3} - \frac{5}{6} t)$ =

(5u⁴ – v²)(5u⁴ + v²) =

(1,5xy² + z³)(1,5xy² – z³) =

(4a – a³)(a³ + 4a) =

(p³ – 0,1r⁴)(p³ + 0,1r⁴) =

$(\frac{a}{2} + \frac{p^{2}}{3}) (\frac{a}{2} - \frac{p^{2}}{3})$ =

(ax + by)(ax – by) – a²(x – y)(x + y) – y²(a – b)(a + b) = 0

(m² + n²)(m² – n²) – (m – n)(m³ + n³) = mn(m – n)(m + n)

Пример. 72 · 68 = (70 + 2)(70 – 2) = 70² – 2² = 4900 – 4 = 4896

42 · 38 =

22 · 18 =

61 · 59 =

46 · 54 =

58 · 62 =

Пример. 72 · 68 = (70 + 2)(70 – 2) = 70² – 2² = 4900 – 4 = 4896

78 · 82 =

105 · 95 =

198 · 202 =

301 · 299 =

94 · 86 =

S =

Если a = 8,5 и b = 4,5, то

S = = (cм²).

S =

Если a = 8,5 и b = 4,5, то

S = = (cм²).

196. Практическая работа

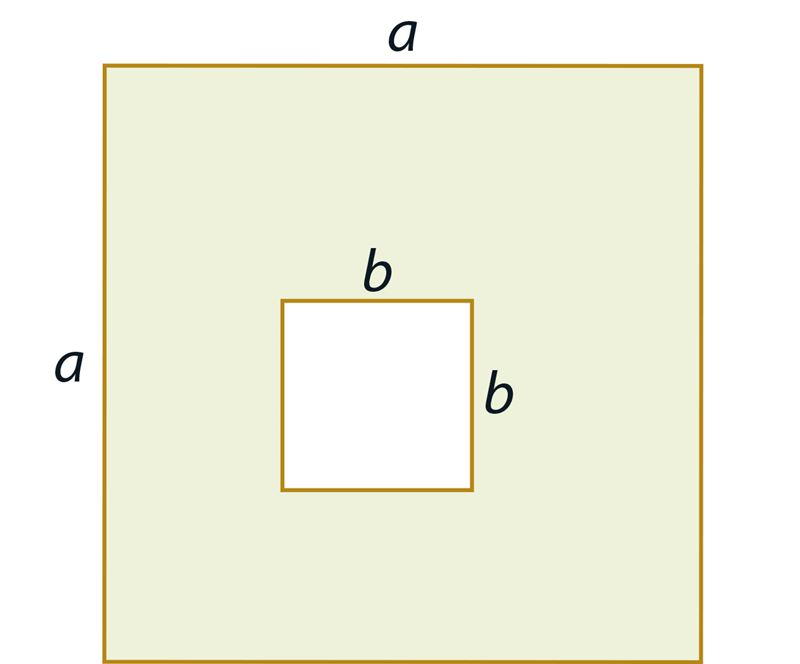
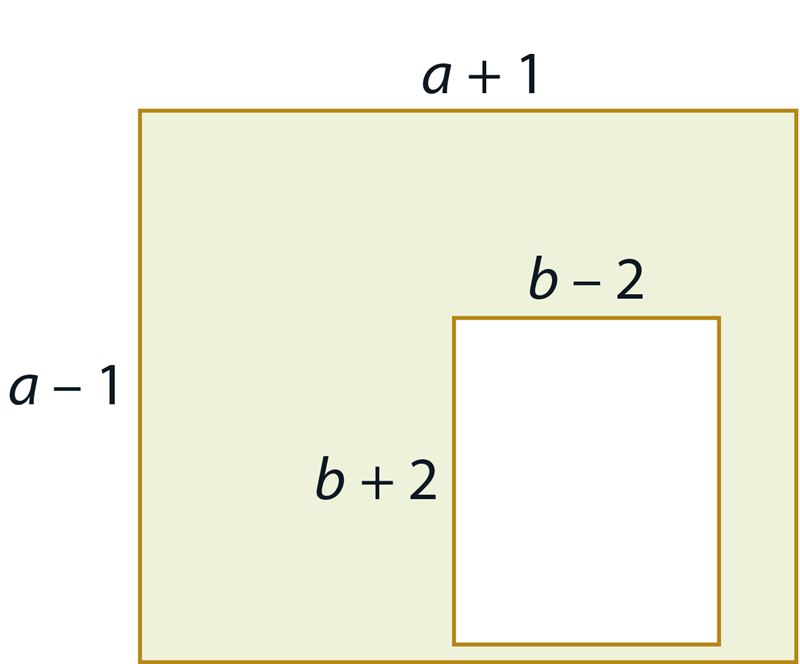
Вырежи из бумаги квадрат. Пусть длина стороны квадрата равна a.
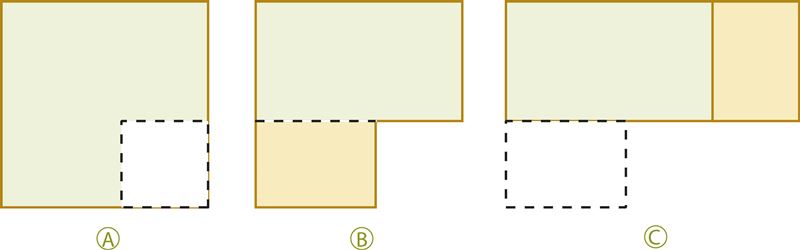
Вырежи из полученного квадрата меньший квадрат. Пусть длина стороны меньшего квадрата равна b (b < a, см. рисунок A).
Разрежь на части закрашенную фигуру и расположи эти части так, как показано на рисунке C. Эта практическая работа позволит тебе обосновать с помощью площадей фигур справедливость формулы $a^{2} - b^{2} = (a + b) (a - b)$ .