Сложение и вычитание многочленов

  1. как к данному числу прибавить сумму чисел, например, как вычислить сумму
    10 + (2 + 6 + 5 + 1);
  2. как из данного числа вычесть сумму чисел, например, как вычислить разность 20 – (5 + 2 + 3 + 6).

Можно ли в этих выражениях отбросить скобки, ничего остального при этом не меняя?

1. Многочлен – это сумма одночленов. Поэтому сложение двух многочленов выполняется так же, как и сложение суммы с числом: члены одного многочлена записываются вслед за членами другого многочлена с теми же знаками, что были у них раньше. Если полученная сумма содержит подобные члены, то нужно выполнить их приведение.

Найдем сумму многочленов 5a – 6b + 7 и 2a – 9b – 5.

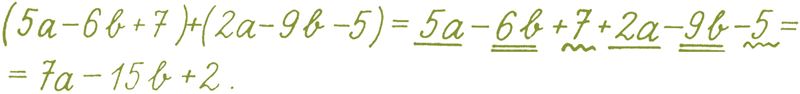
Как мы видим, заключение слагаемых в скобки не имеет значения.

(a + 3) + (a – 4) =  = 

(x + y) + (x – y) =  = 

(6 – b) + (6 + b) =  = 

(c + d) + (c + d) =  = 

(y – 2) + (5 – y) =  = 

(2u – 4) + (u + 1) =  = 

(a – 3b) + (2a + b) =  = 

(4c – 5d) + (4d – c) =  = 

(x2 + 2) + (3x2 – 2) =  = 

(a – y2) + (a + y2) =  = 

2. Вычитание одного многочлена из другого выполняется так же, как и вычитание суммы из числа: к уменьшаемому многочлену нужно прибавить все члены вычитаемого многочлена с противоположными знаками. Если результат содержит подобные слагаемые, то их нужно привести.

Вычтем из многочлена 5a – 6b + 7 многочлен 2a – 9b – 5. Получим:

(y + 5) – (y – 2) =  = 

(3a – 1) – (a + 2) =  = 

(a – 2x) – (x – a) =  = 

(5c – 3) – (2c + 1) =  = 

(t – 3s) – (2t + s) =  = 

(a2 + 1) – (a2 + 3) =  = 

(2u2 – u) – (u – u2) =  = 

(4 + v3) – (v3 + 4) =  = 

(2s2 – s) – (s2 – 2s) =  = 

(x – x3) – (x + 2x3) =  = 

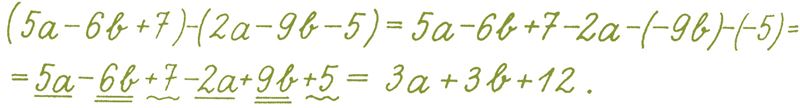
3. Иногда в одном и том же выражении приходится выполнять как сложение, так и вычитание многочленов. Например:

(2x – 5) – (x – 7) + (15 – 9x) – (6x – 3).

В этом случае нужно применять как правило сложения, так и правило вычитания многочленов. Эти правила можно объединить в одно правило раскрытия скобок:

  • чтобы раскрыть скобки, перед которыми стоит знак плюс, надо записать без скобок все члены, стоящие в скобках, с их знаками;
  • ​чтобы раскрыть скобки, перед которыми стоит знак минус, надо записать с противоположными знаками (без скобок) все члены, стоящие в скобках.

Применив это правило, мы можем упростить данное выше выражение следующим образом:

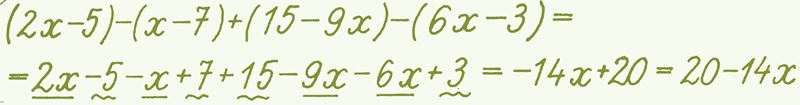
(–a + b) – (b – c) + (a + c) =  = 

(2x – 3y) + (5x – y) – (3x – 4y) =  = 

–5s + 6t + (s + 8t) + (6s – 4t) =  = 

8m – 9n + (2m – n) – (10m – 5n) =  = 

–(a – 2b + c) – 4c + (3a – 2b + 5c) =  = 

z3 + 6z – (z2 – 2z) + (–8z – z3) =  = 

Ще на цю тему
Інші дії

Упражнения A

(8cd – 5d) – (3cd – 4d) = 

(6x – 4x2) + (7x2 – 6x) = 

(–4ax + 5ay) – (3ay + ax) = 

(5x3 + x2) – (6x3 – 4x2) = 

(m2n – 9mn2) + (mn2 – m2n) = 

(0,8a3 + 1,3a2) – (1,2a2 + a3) = 

(2,3x2 – 4x) – (2x + 3x2) = 

(0,5 + 2az) + (–2,2az – 1) = 

(4x – 5y) – (9 – 2x – 5y) = 

(x2 – x + 1) + (2x – 1) = 

(ay – 2y) + (4y – 2a – ay) = 

(a3 + 5a2 + a) – (a + a3) = 

(a + b – c) – (b – c + a) = 

(x – y – z) + (z – y + x) = 

(3x2 – 2x + 5) – (x2 + x + 5) = 

(ax – x + a) – (ax – x + a) = 

(2x + 8y) – (3y – 2x) = 

Если x = –5 и y = 1,2, то значение выражения равно

 = 

(a2 – a) + (2a2 + a) = 

Если a = –4, то значение выражения равно

 = 

(x3 + 4) – (2x3 + 6) = 

Если x = –2, то значение выражения равно

 = 

Ответ: сумма этих многочленов равна .

Ответ: разность этих многочленов равна  .

Ответ: 

Ответ: 

Ответ: длина второго отрезка есть , а сумма длин отрезков равна .

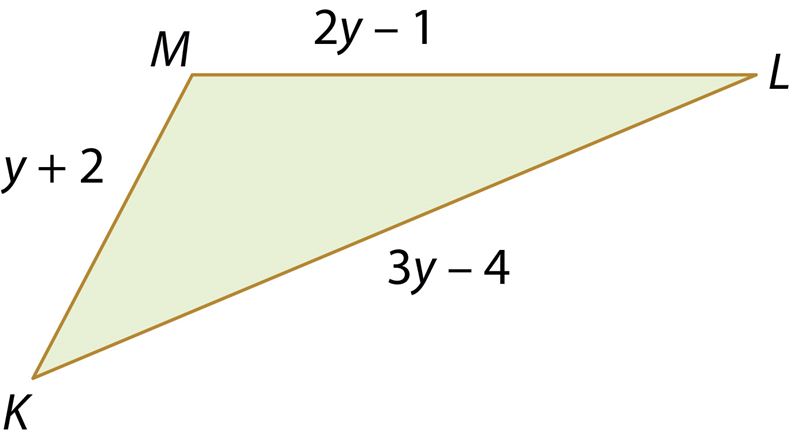Ответ: периметр треугольника KLM выражается в виде P =  и его значение равно .

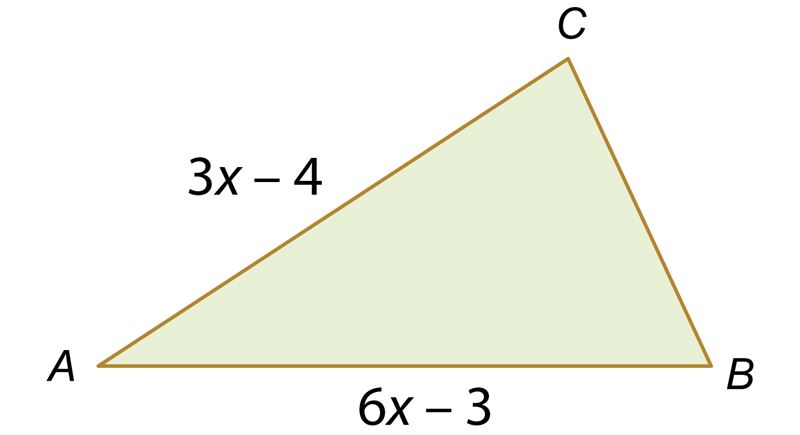
Ответ: BC = . Если x = 8, то AB = , AC = , BC =  и P = .

(3x – 7) – (4x – 3) = 9
x = 

–(4z + 6) = 15 – (z + 21)
z = 

–(5 – 4y) + (7y – 1) = –6
y = 

15x + (17 – 10x) = –(4x + 10)
x = 

4u – (8u + 11) + 29 = 10
u = 

3 – (6t – 18) = t + (t – 11)
t = 

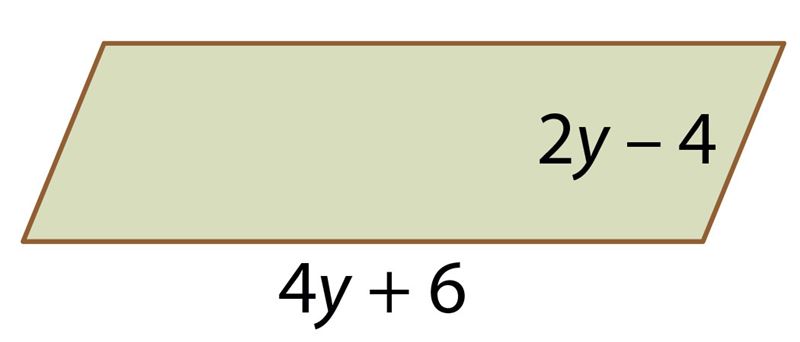
Ответ: y = , P =  единиц.

Ответ: эти числа есть (в порядке возрастания) , , .

Подсказка
Два последо­вательных нату­ральных числа – это n и n + 1.
Ще на цю тему
Інші дії

Упражнения Б

(7ax – 9ay + 4xy) – (5xy + 7xa – 8ya) = 

15a2 – 2a – [3a2 – (2a – 6a2)] = 

4c2 – [(8c2 – 3c) – (3c2 + 6c)] = 

–[(3ax – by) + (ay + 2by)] – [(ax – ay) – (4ax + by)] = 

–(1,5s2 – 2,4s3) – [s2 – (5,2s3 + 2,5s2)] = 

4x3 – [x2 + (2x3 – x2 + x)] = 

Если x = –10, то значение выражения равно

 = 

9a2y + (–5a2y + a2) – (4a2y + y2 – 3a2) = 

Если a = 0,4 и y = –10–1, то значение выражения равно

 = 

(32n – 2 · 3n–1) – (5 · 3n–1 – 4 · 32n) = 

Если n = 1, то значение выражения равно

 = 

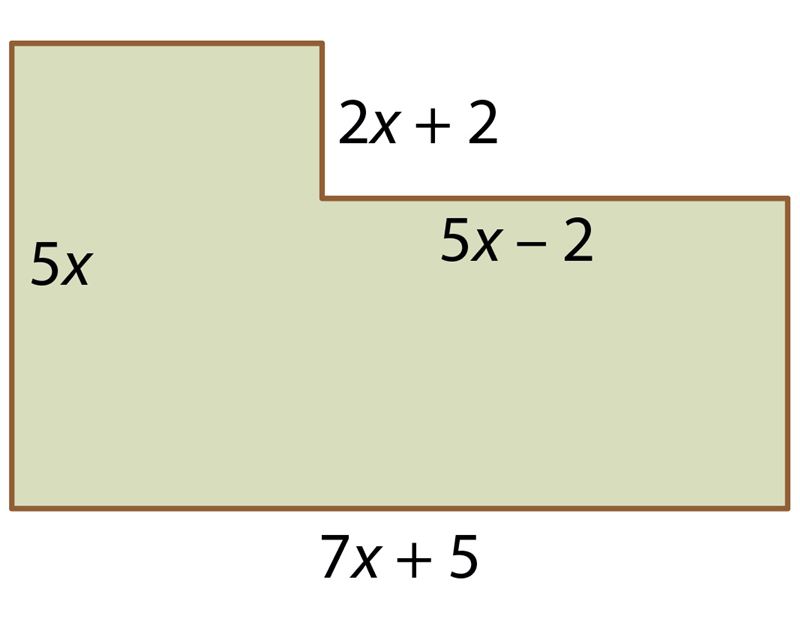
Ответ: периметр многоугольника выражается в виде P = . Если периметр многоугольника равен 58, то x = .

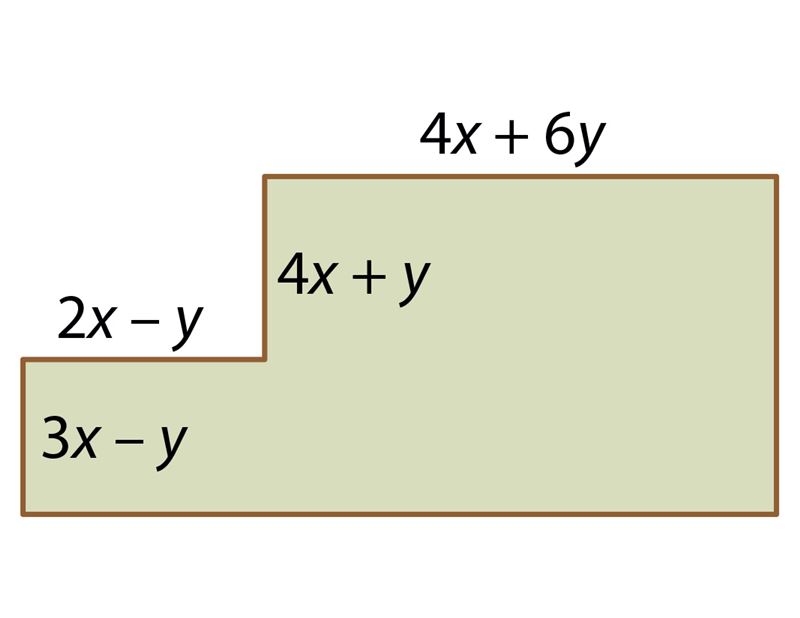
Ответ: неизвестная горизонтальная сторона выражается в виде , неизвестная вертикальная сторона – в виде  и периметр многоугольника – в виде .

Если x = 7 и y = 12, то периметр многоугольника равен .

A + B + C = 

Если x = –1, y = 2 и z = 3, то значение A + B + C равно .

A – B + C = 

Если x = –1, y = 2 и z = 3, то значение A – B + C равно .

A – B – C = 

Если x = –1, y = 2 и z = 3, то значение A – B – C равно .

–A – B – C = 

Если x = –1, y = 2 и z = 3, то значение –A – B – C равно .

Ответ: 

Ответ: искомый многочлен есть .

Ответ: искомый многочлен есть .

(5y2 – 13y) – [(11y2 + 19y) – (6y2 + 8y)] = 240
y = 

34z-25-712z-0,3=5,8-23z+0,9
z = 

–(0,4x – 0,7) + (2,5 – 0,6x) = 0,8x – (3,1 – 1,2x)
x = 

A + (5x3 – 2x + 9) = 6x3 – 2x + 8
A = 

(3,2uv – 1,3v2 – 1) – A = 4,2uv + 0,7v2 + 1
A = 

A – (3,1x2 + 2xy – 5) = 1,9x2 – xy + 5
A = 

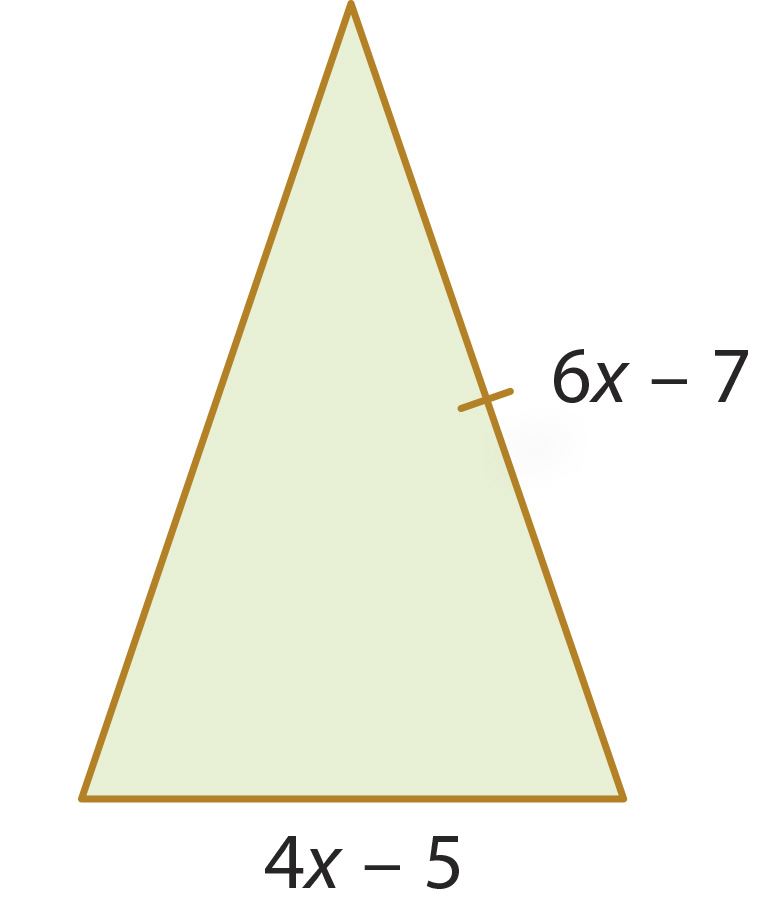
Ответ: основание этого треугольника равно  см и боковая сторона –  см.

Ответ: x = °

Ответ: x = °

Ответ: x = °

Ответ: x = °

Ответ: эти числа есть  и .

Ответ: P =  дм.

Ответ: это число есть .

Подсказка
Общим видом дву­значного числа является 10a + b, где a – цифра десятков и b – цифра единиц. Например, 27 = 10 · 2 + 7.

Ще на цю тему
Інші дії