Пусть даны два уравнения, например, 2x + 3y = 12 и x + y = 5. Изобразим эти уравнения графически.
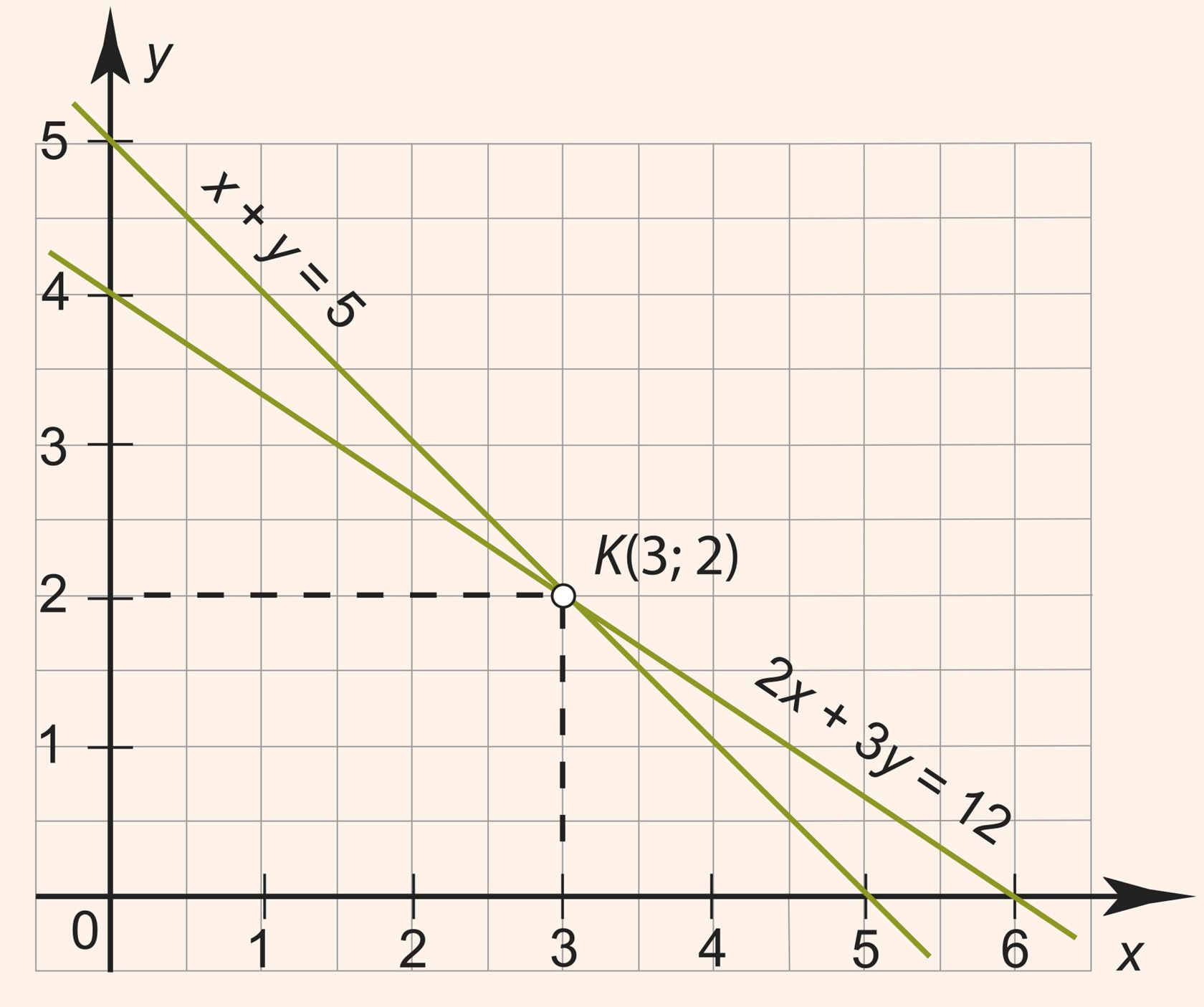
На рисунке видно, что прямые 2x + 3y = 12 и x + y = 5 пересекаются в точке K(3; 2). Но тогда координаты этой точки x = 3 и y = 2 должны одновременно удовлетворять обоим уравнениям, другими словами, числовая пара (3; 2) является общим решением этих уравнений. Так как две непараллельные прямые пересекаются только в одной точке, то других общих решений у этих уравнений нет.
Условие задачи, в которой требуется найти общее решение уравнений 2x + 3y = 12 и x + y = 5, записывается так:
В этом случае говорят, что данные уравнения образуют систему линейных уравнений с двумя неизвестными.
Далее мы будем рассматривать только системы, составленные из двух уравнений. Такая система, записанная в стандартном виде, выглядит следующим образом:
Символы a1, b1, a2, b2, c1, c2 обозначают здесь коэффициенты системы, a буквы x и y – неизвестные.
Общие решения входящих в систему уравнений называются решениями системы. Решить систему – это значит найти все ее решения. Решения системы линейных уравнений с двумя неизвестными можно найти графическим способом. Для этого нужно построить графики уравнений системы (прямые) на одной координатной плоскости. Решениями системы будут координаты общих точек построенных прямых.
 |
||||||||
Решим графически систему уравнений
Изобразим графически оба уравнения системы на одной координатной плоскости.
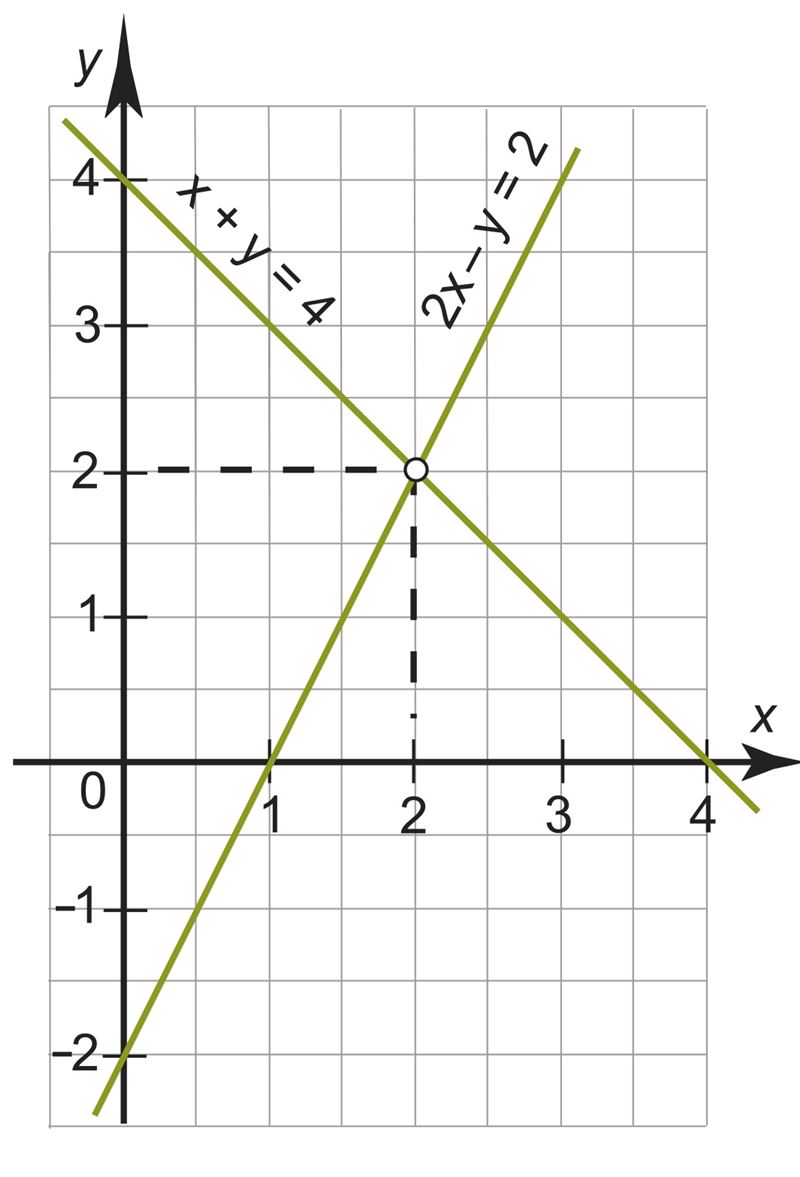
На рисунке видно, что построенные прямые пересекаются в точке (2; 2). Поэтому координаты этой точки удовлетворяют обоим уравнениям системы. следовательно, решение системы можно записать
 |
||||||||
Решим с помощью программы GeoGebra систему уравнений
Для этого сначала запишем в окно ввода первое уравнение и нажмем на ENTER. Таким же образом построим прямую, соответствующую второму уравнению.
 „Точка“ |
||||||||||||||||
 „Пересечение двух объектов” |
||||||||||||||||
Чтобы найти точку пересечения прямых, выберем в меню „Пересечение двух объектов” и щелкнем мышью на обе прямые.
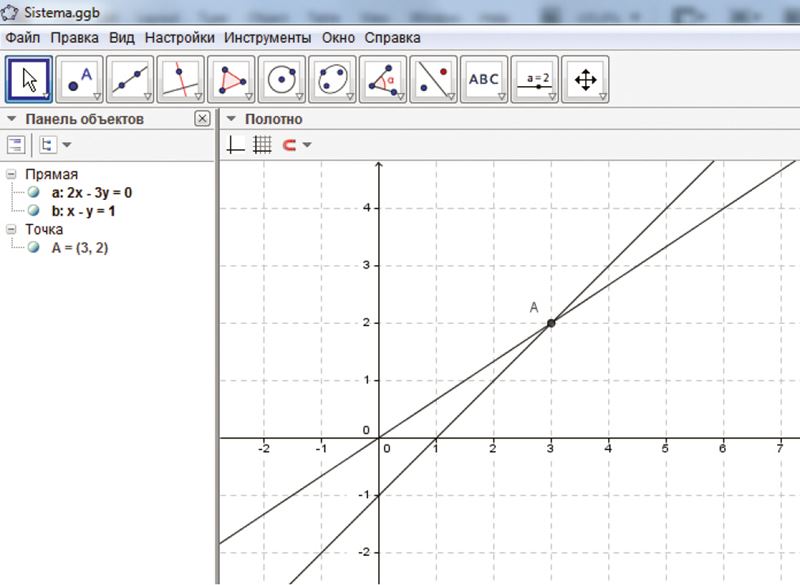
Координаты найденной точки найдем на Панели объектов. Что является решением данной системы уравнений?
Упражнения A
 |
||||||||
- что означает: два уравнения образуют систему;
- что называется решением системы;
- что представляет собой графически решение системы линейных уравнений с двумя неизвестными.
Система уравнений | Решение |
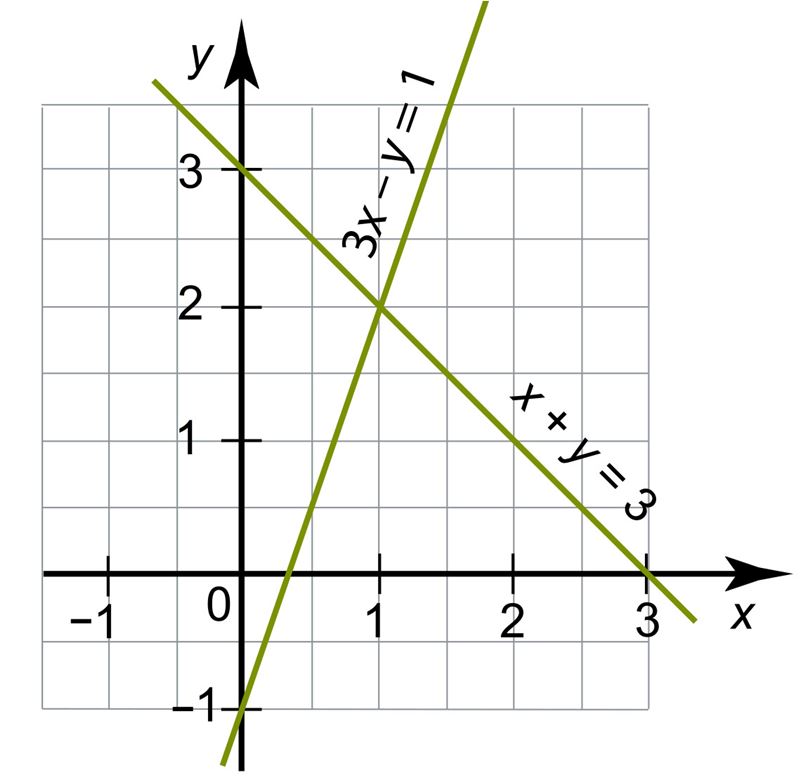
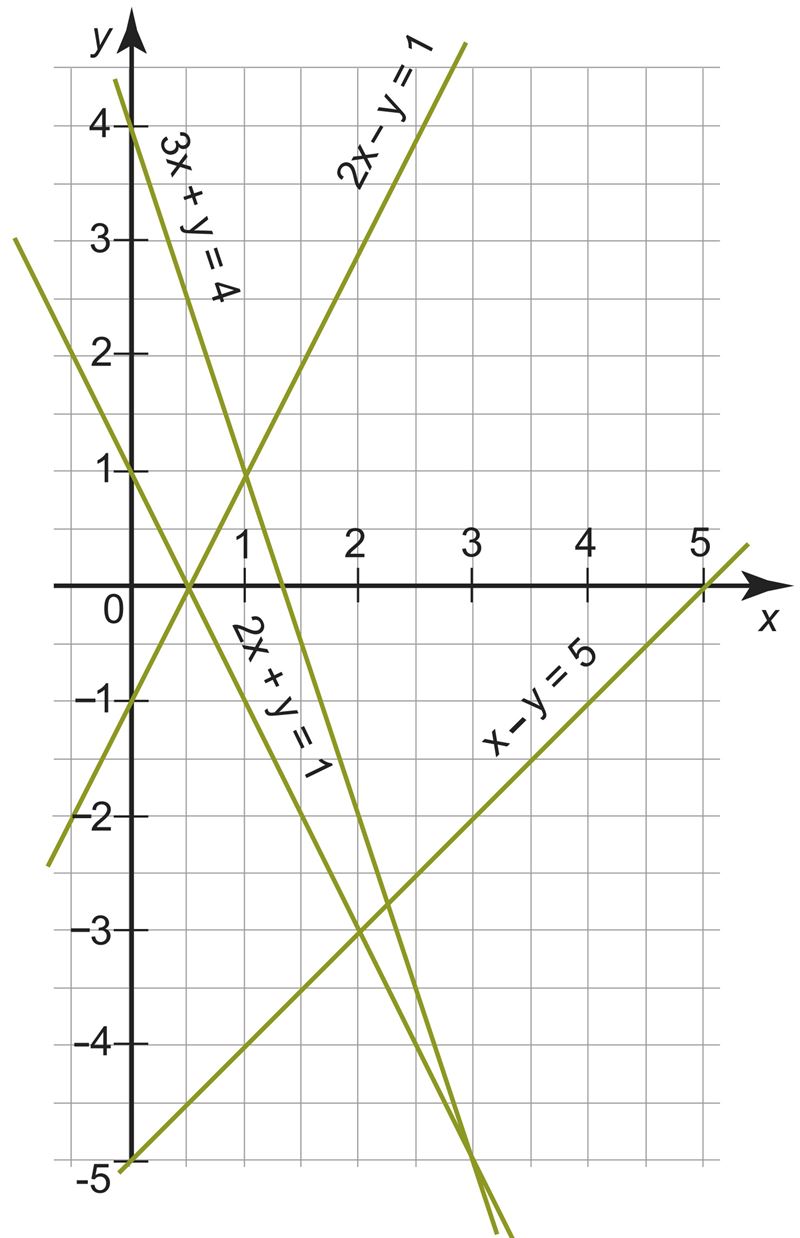
- С помощью рисунка определи, какому из уравнений удовлетворяют следующие координаты точек:
(3; 0) | |
(0; 3) | |
(0; –1) | |
(1,5; 1,5) | |
(0,5; 2,5) | |
(1,5; 3,5) |
- Найди решение системы уравнений с помощью программы GeoGebra.
Ответ: решением этой системы является .
Система уравнений | Решение |
Упражнения Б
 |
||||||||
.
Отметь решения:
- (0; 1)
- (15; –3)
- (–5; 10)
- Удалось ли найти точку пересечения прямых?
- Каково взаимное расположение двух прямых?
Они . - Вырази из каждого уравнения неизвестное y. Сравни в уравнениях системы коэффициенты при неизвестном х и свободные члены. Какую закономерность можно подметить?
Сформулируй полученный вывод: система линейных уравнений с двумя неизвестными не имеет решений, если соответствующие уравнениям прямые.
Подумай, как уравнение прямой в GeoGebra привести к виду y = ax + b.
Заданное решение составленного уравнения | Составленное уравнение |
(0; 2) | |
(3; 0) | |
(1; –2) |
- Удалось ли найти точку пересечения соответствующих уравнениям прямых?
- Каково взаимное расположение двух прямых?
Они . - Вырази из каждого уравнения неизвестное y. Сравни в уравнениях системы коэффициенты при неизвестном x и свободные члены. Какую закономерность можно подметить?
Сформулируй полученный вывод: система линейных уравнений с двумя неизвестными имеет бесконечное множество решений, если соответствующие уравнениям прямые .
