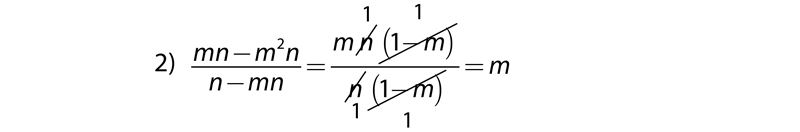Вынесение общего множителя за скобки

1) 6a² + 12a;

2) 8ab³ – 6ab + 4a²b.

Ранее (§ 1.4) мы научились умножать одночлен на многочлен. В задаче 131 нужно решить обратную задачу: как представить заданный многочлен в виде произведения одночлена и другого многочлена? Рассмотрим, например, многочлен

12x³ – 4x² + 8x

и выясним, какие одночлен и многочлен нужно перемножить, чтобы получить данный многочлен. Для этого исследуем, на какой одночлен можно разделить этот многочлен. Таких одночленов несколько, например, 2, 4, x, 2x и др. Возьмем в качестве коэффициента делителя наибольший общий делитель коэффициентов данного многочлена, а переменную возьмем с наименьшим показателем степени. Искомым делителем будет одночлен 4x, и тогда наш многочлен можно записать в виде произведения двух множителей следующим образом:

12x³ – 4x² + 8x = $4 x (\frac{12 x^{3}}{4 x} - \frac{4 x^{2}}{4 x} + \frac{8 x}{4 x})$ = 4x(3x² – x + 2).

Промежуточную часть обычно не записывают, вычисляя соответствующие частные в уме.

Мы преобразовали данный многочлен в произведение. Преобразование многочлена в произведение называют разложением многочлена на множители. При разложении на множители мы пока будем пользоваться следующим приемом:

найдем общий делитель всех членов многочлена, т. е. одночлен, на который делятся все члены многочлена;
найденный делитель запишем перед скобками (или за ними), т. е. вынесем его за скобки;
в скобках запишем многочлен, который получится при делении заданного многочлена на вынесенный за скобки множитель.

6m²n⁵ + 10m³n² – 8m⁵n³ = 2m²n²(3n³ + 5m – 4m³n)
12a²b² + 8a³ – 4a² = 4a²(3b² + 2a – 1)
x²y² – 2x²y³ + x³y³ = x²y²(1 – 2y + xy)

Правильность разложения на множители можно всегда проверить, снова раскрыв скобки, т. е. с помощью умножения.

Упражнения A

	6a – 6b	18x + 12
число 2;
число 3;
число 6.

Не пользуйся пробелами!

	24y – 6	30 + 12y
число 2;
число 3;
число 6.

Не пользуйся пробелами!

	30a + 18	42 – 6t
число 2;
число 3;
число 6.

Не пользуйся пробелами!

	60 + 12z	48x – 54
число 2;
число 3;
число 6.

Не пользуйся пробелами!

	–4ay – 4ax	20a² – 8a	–12az + 16a
множитель –4;
множитель a;
множитель –4a.

Записывай без пробелов! Показатель степени квадрата вводи либо после символа ^, либо с помощью кода Alt+0178 или же копируй отсюда: ².

	4a + 24ax	32a – 8a³	–16am – 40an
множитель –4;
множитель a;
множитель –4a.

Записывай без пробелов! Показатели степени квадрата и куба вводи после символа ^ или с помощью кодов Alt+0178 и Alt+0179, либо копируй отсюда: ², ³.

	28a + 20ab	–12a³ – 4a	12ab – 4a
множитель –4;
множитель a;
множитель –4a.

	xy² – x²y	xy + x²y²
множитель x;
множитель y;
множитель xy.

Не пользуйся пробелами! Показатель степени квадрата вводи после символа ^ или с помощью кода Alt+0178, либо копируй отсюда: ².

	x³y + xy²	x³y³ – 2xy
множитель x;
множитель y;
множитель xy.

Наибольший общий делитель (НОД) чисел – это наибольшее число, на которое делятся все данные числа. Например, наибольшим общим делителем чисел 12 и 18 является 6.

10x – 15y =

18a + 12 =

24m – 16n =

20y + 30z =

–8c + 12d =

14x – 28 =

21p + 15r =

–6s – 9t =

x³ – x² =

y⁴ + y =

a⁵ – a⁴ =

z³ – z⁴ =

a²b + a²b² =

m³n² – m³n³ =

p²r + pr³ =

s² – s³t =

2a – 2y =

7x + 14 =

ax – a =

4m – 8 =

xy + y =

6m + mn =

–x² – 2x =

cd – bc =

a² + 4a =

5u² – 3u =

3a + 6ab =

8y² – 4y =

9x – 6x² =

2cd + 4d =

5z – 10z³ =

7y⁴ – 14y² =

s³t + s²t² =

b²y – by =

12c² – 6c³ =

4m – 12m² =

4a²y + 12ay² =

8x³y – 6x²y =

14mn⁴ – 21m²n³ =

13s²t⁵ + s³t⁴ =

22b³c³ – 2b³c² =

15c⁴ – 20c²d =

16 + 24ax =

18xy³ – 9y⁴ =

–c³y² – 4c³y³ =

6uv² + 12u²v² =

13m⁴u + 26m³n² =

18u²v⁵ – 27uv⁴ =

28t² – 4t³s =

12p²r + 24p³r² =

9a²x³ – 15ax² =

ab + ac – ad =

mx – nx – px =

5u + 10s + 15vs =

8c – 4d + 12b =

–xy – zx + xux =

a³ – a² – a =

a⁴ + a³ + a² =

x⁶ + x³ – x² =

c⁴ – c⁵ + c⁷ =

y³ – y⁶ – y⁸ =

2x³ – 6x² – 14x =

a²b + a²b² + ab² =

15m⁵ – 12m⁴ + 9m² =

x³y³ – x²y³ – x²y² =

16c – 24c² + 32c⁴ =

6 · 25,4 + 34,6 · 6 = =

15 · 3,7 + 15 · 6,3 = =

0,51 · 107 – 0,51 · 7 = =

8 · 46,2 – 6,2 · 8 = =

0,53 · 7 + 7 · 0,27 = =

6,12 · 14 – 1,12 · 14 = =

Если x = 8,7 и y = 1,3, то значение выражения 8x + 8y равно

Если a = 13,8 и b = 3,8, то значение выражения 11a – 11b равно

Если x = 0,45, то значение выражения 1,45x – x² равно

Упражнения Б

16xy⁵ + 12x⁵y⁵ – 4xy⁴ =

24a²b³ + 18a²b² – 12a²b⁴ =

25a⁵b³ – 15a³b³ – 20a³b⁵ =

42u⁶v⁴ – 18u⁵v³ + 30u³v² =

15a²b³c⁴ – 25a⁴b³c² + 40a⁴b⁴c⁴ =

28u⁸s⁴t² + 21s⁶t⁸u² – 14s⁵t⁶u⁶ =

18m⁵n⁶p⁷ – 24m⁴n⁵p⁶ + 48m⁵n⁶ =

56x⁵y⁶z² + 42x⁵y⁶z³ – 84x³y³z² =

4(x – 3) + a(x – 3) =

c(a + b) – 3(a + b) =

2m(x – y) – n(x – y) =

u(2m + 1) + v(2m + 1) =

a(n + 2) + 3b(n + 2) =

5u(s – 4t) – 2v(s – 4t) =

3x(2a + 3b) + y(2a + 3b) =

p²(n² – m) – s(n² – m) =

Если a = 1,4, то значение выражения a³ – 2,4a² равно

Если x = –2,5, то значение выражения 8x³ – 4x² + 6x равно

Если x = $\frac{2}{3}$ и a = –5, то значение выражения 3x²(a + 6) – 2x²(a + 6) равно

$\frac{25^{2} - 25 \cdot 19}{24 \cdot 12 - 48}$ =

$\frac{11 \cdot 19 + 19^{2}}{38 + 3 \cdot 19}$ =

$\frac{10^{7} - 10^{5}}{10^{4} - 10^{3}}$ =

$\frac{3^{8} - 2 \cdot 3^{7} + 5 \cdot 3^{6}}{3^{5} - 3^{4}}$ =

$\frac{39 \cdot 61 + 61^{2}}{8 \cdot 25 - 25 \cdot 4}$ =

$\frac{5 \cdot 2^{10} - 7 \cdot 2^{8} + 2^{7}}{2^{8} + 2^{7}}$ =

Примеры.

Числитель дроби является суммой одночленов. Чтобы разложить эту сумму на множители, вынесем за скобки общий множитель одночленов 2a². Затем сократим дробь. Запомни, что сокращать можно только множители.

$\frac{a b + a c}{2 a}$ = $\frac{}{}$

$\frac{a b + b c}{b}$ = $\frac{}{}$

$\frac{a b^{2} - 2 a^{2} b}{a^{2} b^{2}}$ = $\frac{}{}$

Примеры.

$\frac{a b + a c}{b x + x c}$ = $\frac{}{}$

$\frac{a^{2} b^{3} - a b}{a b^{2} - 1}$ = $\frac{}{}$

$\frac{a b^{2} - a b}{a^{2} b^{2} - a^{2} b}$ = $\frac{}{}$

Примеры.

$\frac{a^{2} - a}{a b - b}$ = $\frac{}{}$

$\frac{2 m n^{2} + m n}{2 n + 1}$ = $\frac{}{}$

$\frac{3 u^{2} v - 9 u v^{2}}{t u - 3 t v}$ = $\frac{}{}$

Вынесение общего множителя за скобки

More like this

Упражнения A

More like this

Упражнения Б

More like this

Opiq score

	Tasks
	Chapter is studied

Вынесение общего множителя за скобки

More like this

Упражнения A

More like this

Упражнения Б

More like this

Add content

Files to be added

Report Mistake

Only report errors related to the functionality or content of Opiq. Please describe the error as precisely as possible.

If you agree to share additional info, add your contact data (e-mail, phone).

Check to help us fight spam

Opiq uses cookies