Средняя линия трапеции

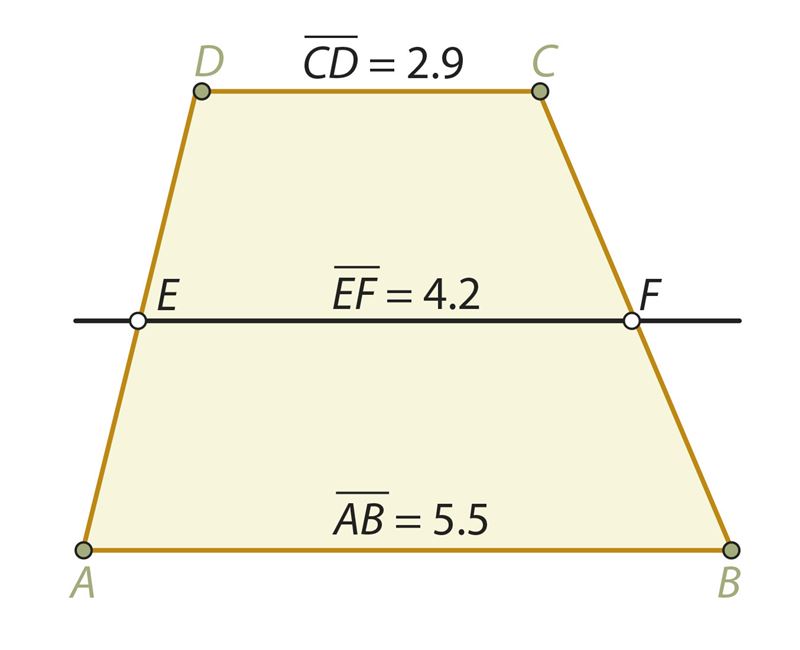
Начертим трапецию ABCD и проведем отрезок, соединяющий середины E и F боковых сторон трапеции (см. рисунок). Отрезок EF (а также его длина) – это средняя линия трапеции.

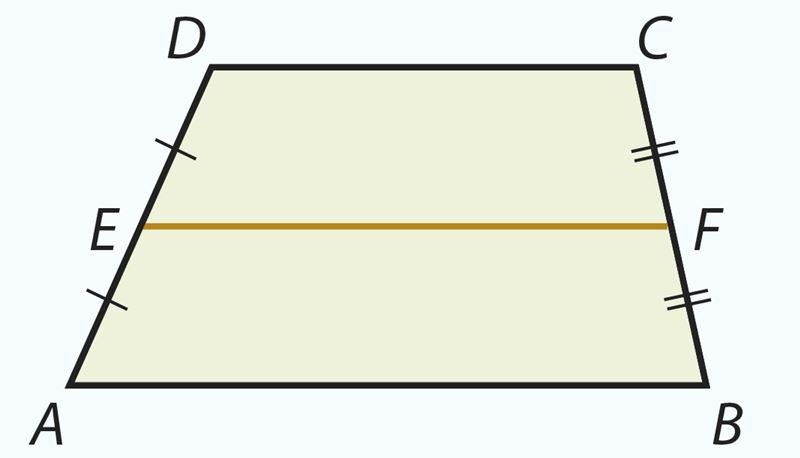Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции.

Свойства средней линии трапеции выражает следующая теорема.

Средняя линия трапеции параллельна основаниям и равна их среднему арифметическому (полусумме).

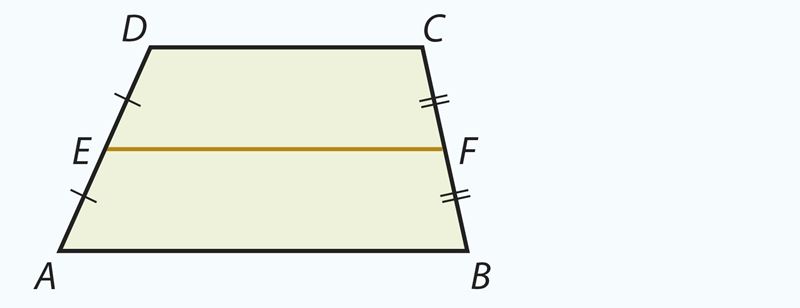
Условие. Отрезок EF – средняя линия трапеции, AE = ED и BF = CF.

Заключение. 1) $E F = \frac{A B + D C}{2}$ ; 2) EF || AB || DC.

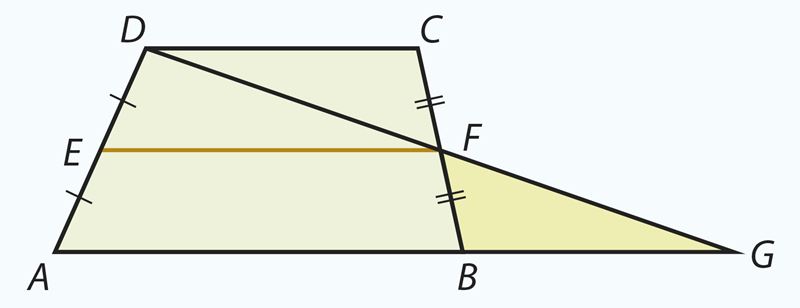
Доказательство. Дополним чертеж. Проведем через вершину D и середину F боковой стороны BC прямую. Она пересекает прямую AB в некоторой точке G. Проследи внимательно ход дальнейших рассуждений.

∠DFC = ∠BFG – вертикальные углы.
∠DCF = ∠FBG – внутренние накрест лежащие углы, образованные пересечением параллельных прямых DC и AB прямой ВС.
ΔDCF = ΔGBF – признак равенства треугольников УСУ.
DF = FG – соответственные стороны равных треугольников.
Отрезок EF является средней линией треугольника AGD – по определению средней линии треугольника.
EF || AB || DC – свойство средней линии треугольника, теорема 1, § 4.2. Таким образом, одна часть заключения теоремы доказана.
BG = DC (см. пункт 3 доказательства).
$E F = \frac{A B + B G}{2}$ – свойство средней линии треугольника.
$E F = \frac{A B + D C}{2}$ – следует из пунктов 7 и 8. ■

Из доказанной теоремы следует, что с помощью средней линии можно вычислить площадь трапеции.

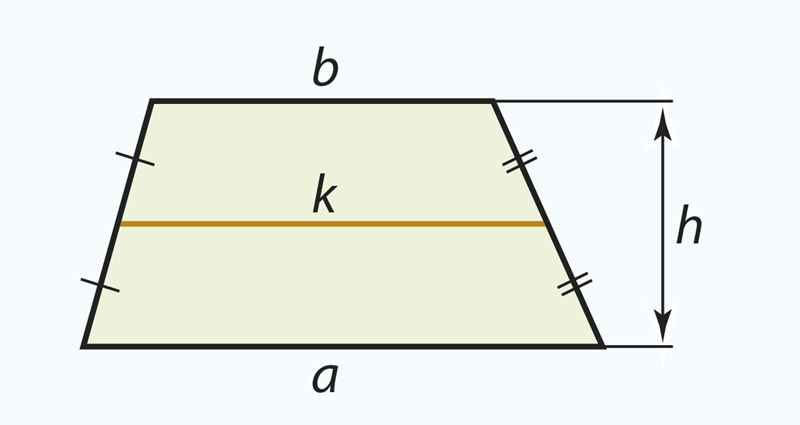
Действительно, площадь трапеции выражается по формуле $S = \frac{a + b}{2} \cdot h$ и $\frac{a + b}{2}$ – это средняя линия k трапеции.

Следовательно

площадь трапеции равна произведению ее средней линии на высоту.

S = kh

Упражнения A

Постарайся самостоятельно сделать нужный чертеж и доказать теорему.

707.3 GeoGebra

Теорема. Средняя линия трапеции параллельна основаниям и равна их среднему арифметическому (полусумме).

Убедись с помощью программы GeoGebra в справедливости свойств средней линии трапеции.

Начерти трапецию. Для этого проведи две параллельные прямые, затем две непараллельные прямые, пересекающие две первые прямые. Найди точки пересечения прямых. Все это ты уже умеешь делать.

«Многоугольник»

Теперь построй с помощью найденных четырех точек трапецию с помощью инструмента «Многоугольник». Чтобы чертеж был нагляднее, сотри лишние части прямых (щелкни правой кнопкой мыши в любую точку прямой и воспользуйся командой «Показать/скрыть объект»).

Далее найди середины E и F соответственно боковых сторон AD и BC трапеции и проведи через одну из этих точек прямую, параллельную прямой AB. На чертеже видно, что эта прямая проходит через середину другой боковой стороны. какой вывод из этого следует? Найди также длины оснований и средней линии трапеции.

«Перемещать»

Наконец, выбери инструмент «Перемещать» и потяни за одну из вершин трапеции. Ты увидишь, что параллельность и соотношения между длинами при этом не изменяются.

Основания трапеции	Средняя линия трапеции
4 см и 12 см	см
26 см и 24 см	см
1,4 дм и 0,6 дм	дм

Основания трапеции	Средняя линия трапеции
15 м и 23 м	м
9 см и 16 см	см
2 дм и 6 см	см

Основания трапеции	Средняя линия трапеции
15,6 дм и 42,2 дм	дм
0,82 м и 2,84 м	м

Основания трапеции	Средняя линия трапеции
74 см и 3,6 дм	дм
246 см и 1,58 м	м

a	b	k
4 дм	дм	5 дм
дм	12 дм	14,5 дм
9,3 дм	87 см	см

a	b	k
0,34 м	дм	4,3 дм
км	0,84 км	910 м
5,3 см	47 мм	см

через основания и высоту;
через среднюю линию и высоту.

k	9 см	0,4 дм	12 см	2,8 м
h	6 см	8 см	1 дм	20 дм
S	см²	см²	дм²	дм²

a = 24 см, b = 42 см и h = 23 см
S = см²

k = 15,6 дм и h = 9 дм
S = дм²

a = 66 м, b = 124 м и h = 54 м
S = м²

k = 4,7 см и h = 32 мм
S = см²

a = 38 см, b = 2,6 дм и h = 0,25 м
S = дм²

k = 7,3 м и h = 64 дм
S = м²

k	h	S
46 см	см	1610 см²
дм	5,8 дм	43,5 дм²

k	h	S
дм	1,5 м	138 дм²
4,4 дм	см	1584 см²

Ответ: основания трапеции равны см и см.

Ответ: основания трапеции равны дм и дм.

Ответ: основания трапеции равны м и м.

Ответ: основания трапеции равны см и см.

∠A = °

∠B = °

∠C = °

∠D = °

∠A = °

∠B = °

∠C = °

∠D = °

∠A = °

∠B = °

∠C = °

∠D = °

Ответ: длина меньшего основания есть единиц, длина большего – единиц, а средняя линия составляет единиц.

Ответ: длина меньшего основания равна ед. длины, длина большего основания – ед. длины и длина средней линии – ед. длины.

Ответ: длина меньшего основания равна ед. длины, длина большего – ед. длины и длина средней линии – ед. длины.

S = единичных квадратов

S = ед. квадр.

Упражнения Б

Ответ: периметр трапеции равен дм.

Ответ: основания трапеции равны см и см.

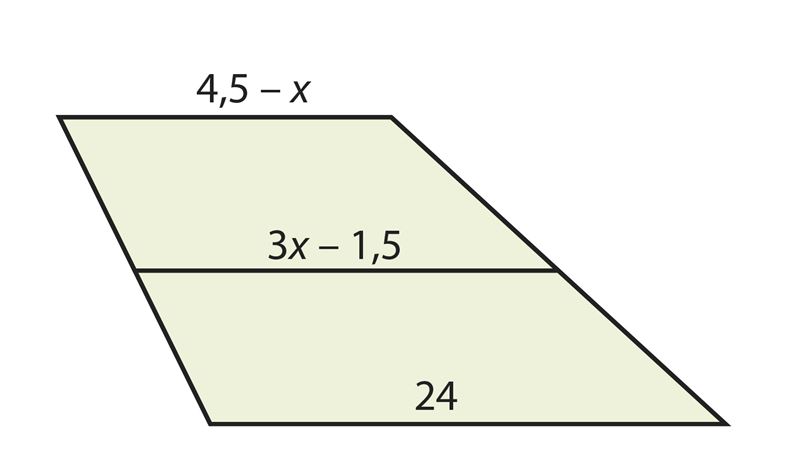
Площадь трапеции равна 330 см², высота – 15 см, а меньшее основание составляет $\frac{2}{3}$ большего основания. Найди основания трапеции.

Ответ: основания трапеции равны см и см.

(См. также задание 639.)

Ответ: диагональ делит среднюю линию на отрезки длиной (по возрастанию) см и см.

Ответ: основания трапеции (по возрастанию) равны см и см.

Ответ: основания трапеции (по возрастанию) равны дм и дм.

Ответ: расстояние между серединами диагоналей трапеции равно см.

Ответ: площади полученных трапеций (по возрастанию) см² и см².

Ответ: средняя линия делится на отрезки длиной см и см.

Эта призма имеет вершин и граней.

Ответ: S_полн = см²; V = см³.

Формулы

S_полн = 2S_осн + S_бок
V = S_оснH
S_бок = PH
S_осн– площадь трапеции
P – периметр трапеции

Эта призма имеет вершин и граней.

Ответ: S_полн = дм²; V = дм³.

Формулы

S_полн = 2S_осн+ S_бок
V = S_оснH
S_бок = PH
S_осн – площадь трапеции
P – периметр трапеции

Ответ: канава вмещает м³ воды.


$\frac{}{}$	$\frac{}{}$	$\frac{}{}$	$\frac{}{}$	$\frac{}{}$


$\frac{}{}$	$\frac{}{}$	$\frac{}{}$	$\frac{}{}$	$\frac{}{}$

739. GeoGebra

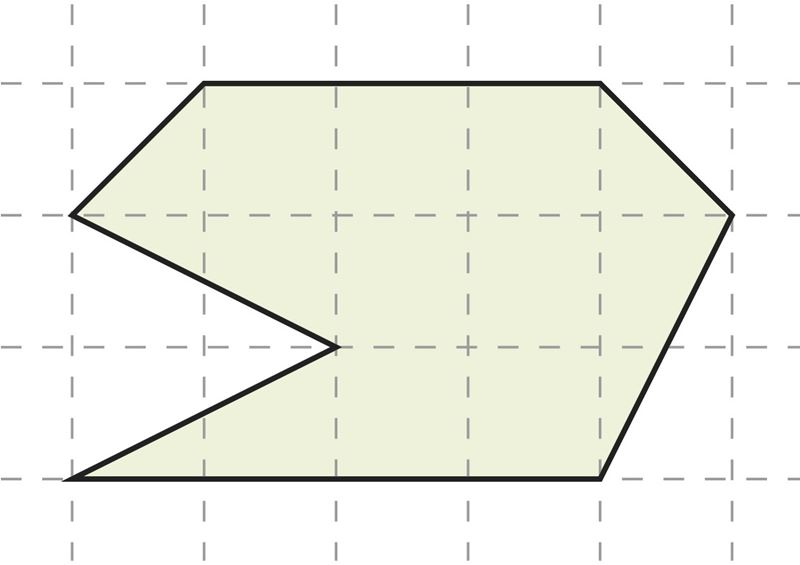
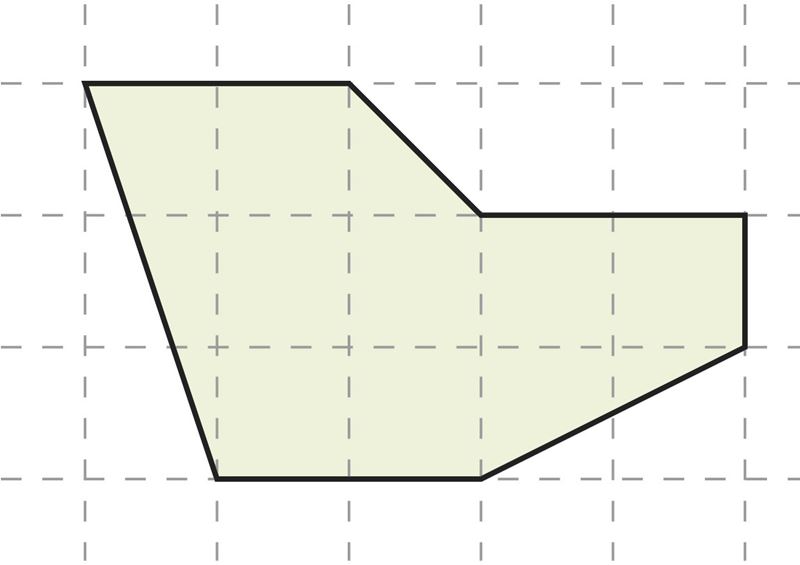
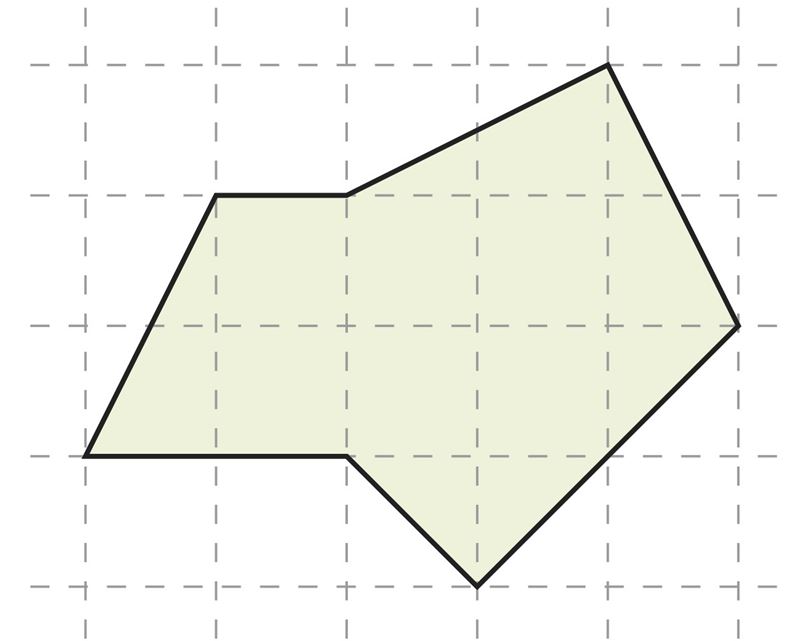
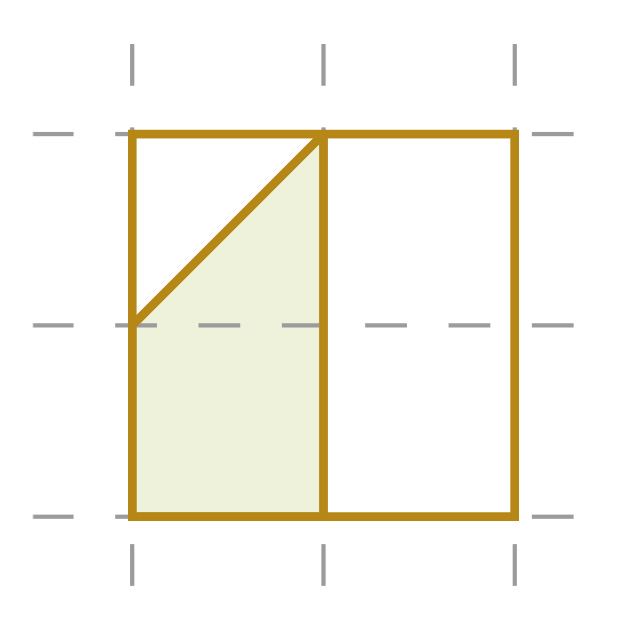
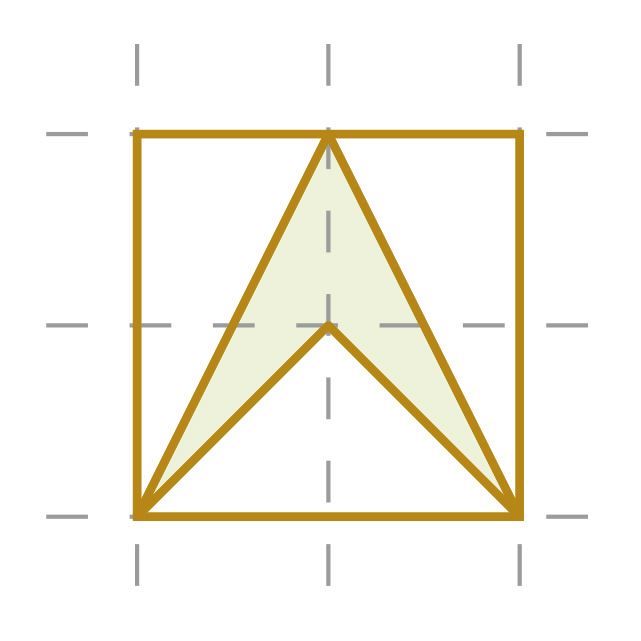
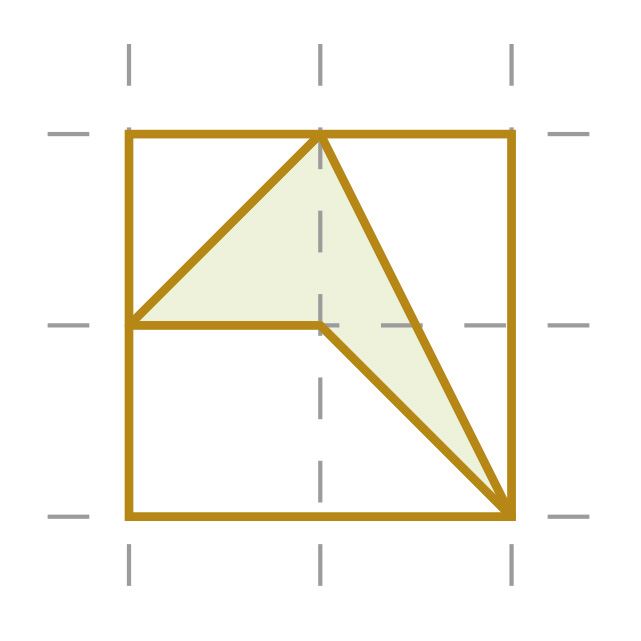
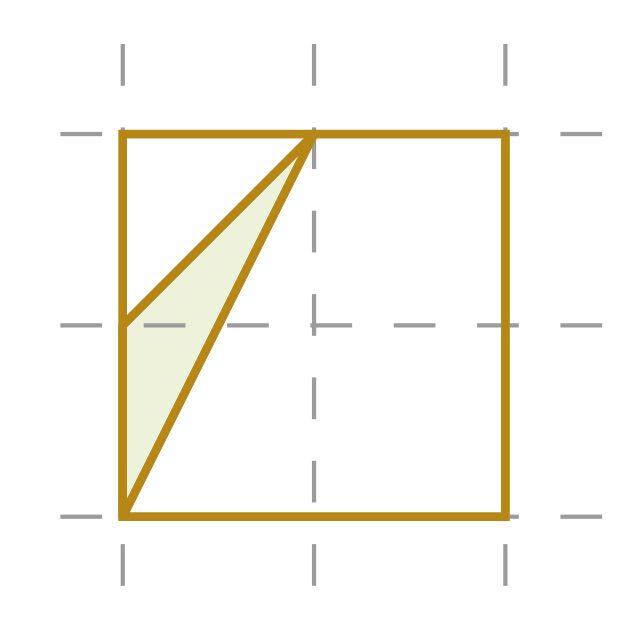
С помощью программы GeoGebra начерти на фоне сетки произвольный многоугольник. Найди площадь этого многоугольника, разбив его на части, площади которых ты умеешь вычислять. В качестве единицы площади возьми одну клетку сетчатого разбиения полотна. Проверь свой результат также с помощью инструмента «Площадь».

«Площадь»

Если вершины многоугольника расположены в вершинах единичных квадратов, то площадь многоугольника можно найти и следующим образом.

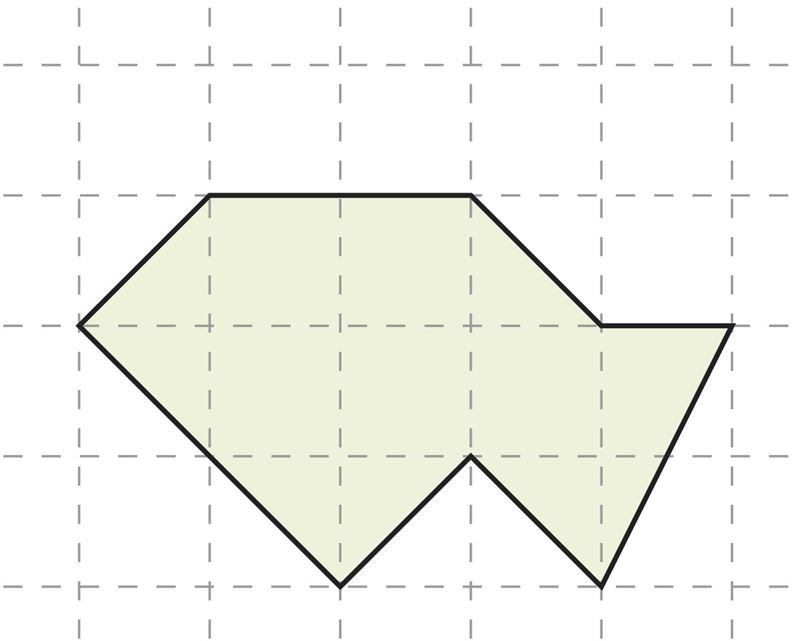
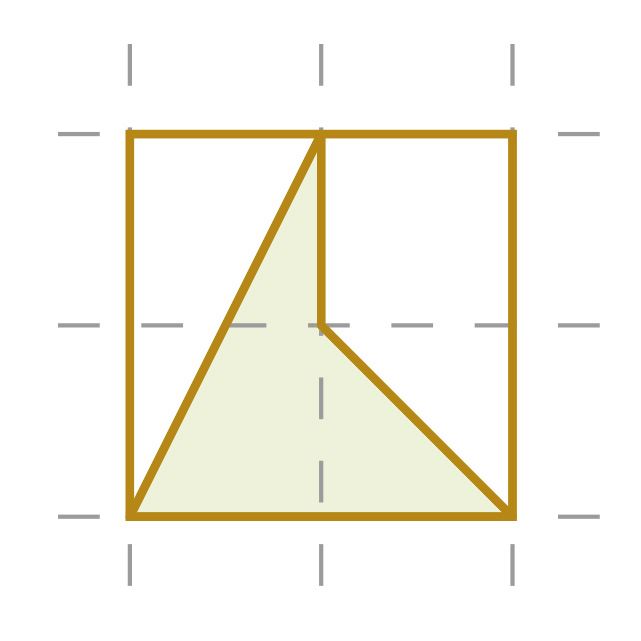
Подсчитай, сколько вершин единичных квадратов расположены на сторонах многоугольника и сколько этих квадратов целиком расположены внутри фигуры. На рисунке справа ты получишь соответственно числа k = 6 и s = 11.

Площадь многоугольника можно теперь найти по формуле $S = \frac{k}{2} + s - 1$ .

Площадь изображенной на рисунке фигуры $S = \frac{6}{2} + 11 - 1 = 13$ (единиц площади).

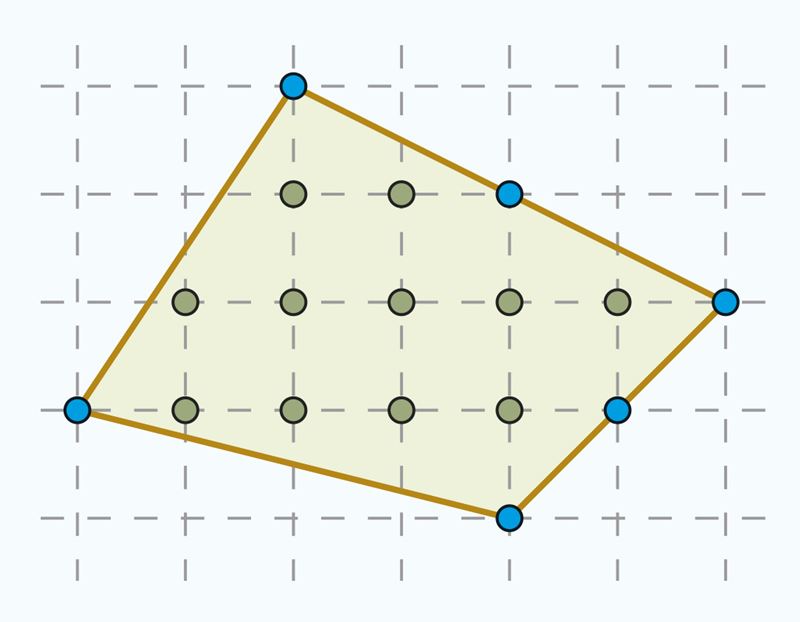Эта формула называется формулой Пика.

Средняя линия трапеции

More like this