Познакомимся еще с одним приемом, который позволяет сводить решение системы линейных уравнений с двумя неизвестными к решению одного линейного уравнения с одним неизвестным. Этот прием называется способом подстановки.
 |
||||||||
Решим систему уравнений
В первом из уравнений системы неизвестное x выражено через другое неизвестное y. Подставим (отсюда и происходит название способа) во второе уравнение вместо x выражение 2y:
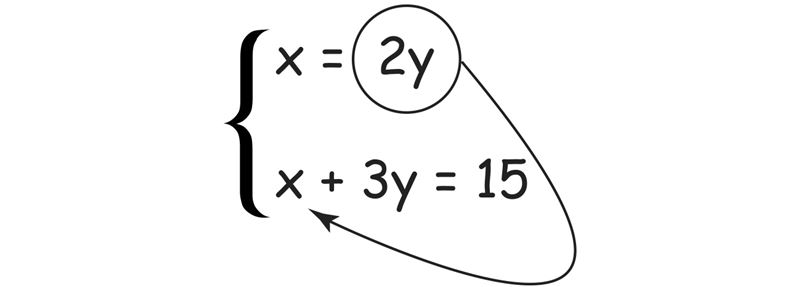 | ||||||||
В результате получим линейное уравнение с одним неизвестным
Подставив найденное значение y в первое уравнение, найдем значение неизвестного x:
x = 2 · 3 или x = 6.
Мы получили пару чисел
Проверка показывает, что пара чисел (6; 3) действительно является решением данной системы уравнений.
 |
||||||||
Решим способом подстановки систему уравнений
В отличие от предыдущего примера, в котором одно из неизвестных уже было выражено через другое неизвестное (x = 2y), нам придется сначала выразить в одном из уравнений одно неизвестное через другое. При этом безразлично, в каком из уравнений и какое неизвестное будет выражаться через другое. Выразим, например, из второго уравнения неизвестное y:
Теперь действуем аналогично примеру 1: подставим в первое уравнение системы вместо y выражение . Получим:
Чтобы избавиться от дроби, умножим обе части последнего уравнения на 4 и получим:
Неизвестное y найдем из уравнения , заменив в нем неизвестное x его значением 2:
.
Проверка.
v1 = 2 · 2 + 3 · 1 = 7; v1 = p1.
v2 = 3 · 2 – 4 · 1 = 2; v2 = p2.
Ответ: