Võrratuse lahendid
Võrratuse lahendid
- Võrratuse lahenditeks on need muutuja väärtused, mille korral võrratus on tõene.
- Võrratuse kõik lahendid moodustavad võrratuse lahendihulga.
- Võrratused on samaväärsed, kui neil on üks ja sama lahendihulk.
Märka
Sulgude kasutamine
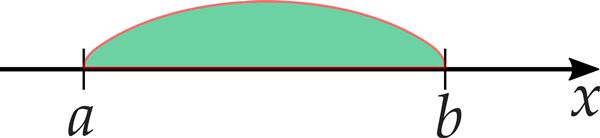
- Kui piirkonna otspunkt kuulub piirkonda, siis on nurksulgude otsad pööratud selle kõrval oleva väärtuse poole:
lõik [a; b].
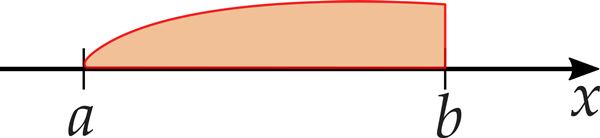
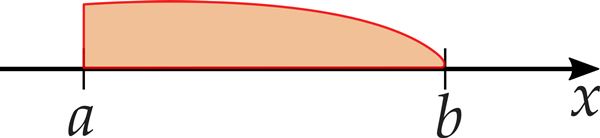
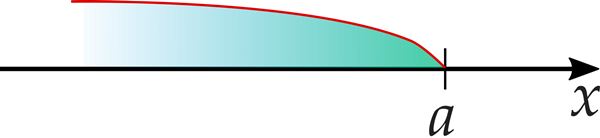
- Kui piirkonna otspunkt ei kuulu piirkonda, siis on kaks võimalust:
- nurksulgude otsad on pööratud sellest väärtusest eemale (Avita paberõpikus):
vahemik ]a; b[; - kasutatakse kumersulge (siin digiõpikus):
vahemik (a; b).
Võrratus | Sulgude abil |
; | |
; | |
; | |
; | |
; | |
; |
Harjuta ja treeni
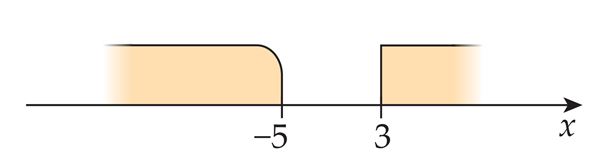
- (–5; 3]
- (–∞; –5) U [3; ∞)
- (–∞; –5] U (3; ∞)
- ℝ\[–5; 3)
- ℝ\(–5; 3]
- ℝ\(–5; 3]
- x <–5 ∨ x > 3
- x <–5 ∨ x ≥ 3
- x ≤–5 ∨ x ≥ 3
- x ≤–5 ∨ x > 3
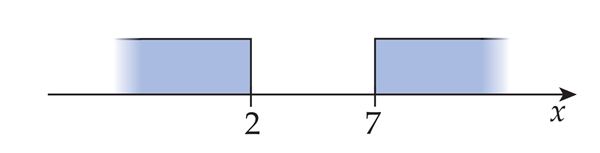
- [2; 7]
- (–∞; 2) U (7; ∞)
- (–∞; 2] U [7; ∞)
- ℝ\[2; 7]
- ℝ\(2; 7]
- ℝ\(2; 7)
- x < 2 ∨ x > 7
- x < 2 ∨ x ≥ 7
- x ≤ 2 ∨ x ≥ 7
- x ≤ 2 ∨ x > 7
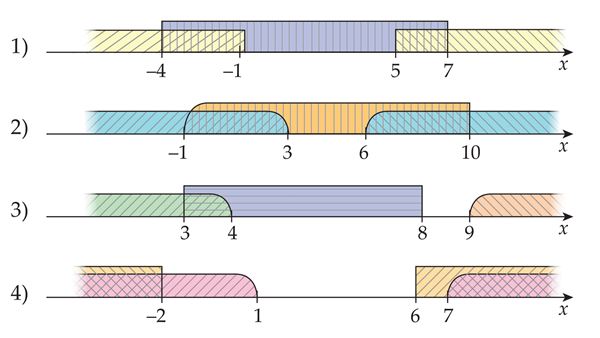
Ühend | Ühisosa |
1) | ;∪; |
2) | ;∪; |
3) | |
4) |