Ruutjuur

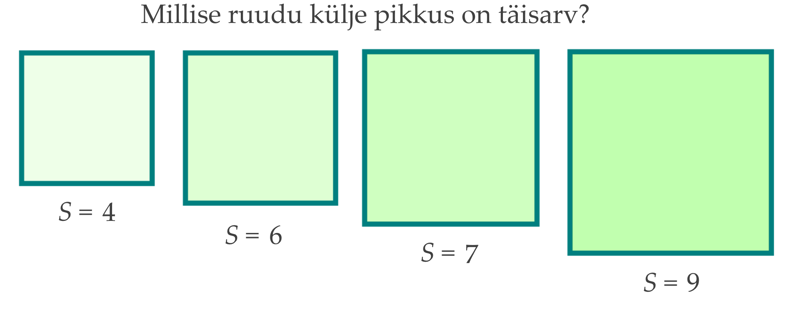
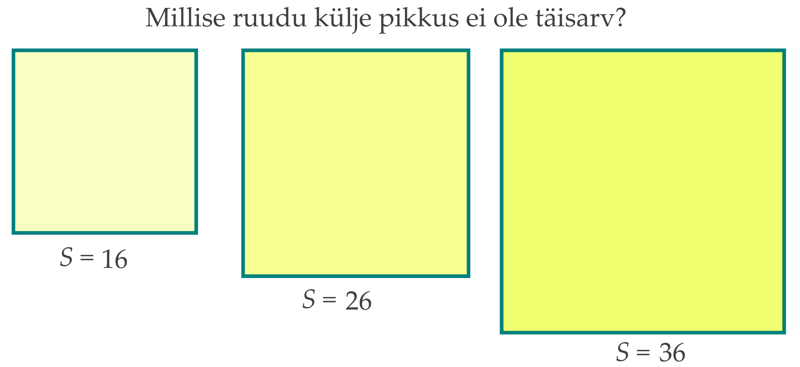
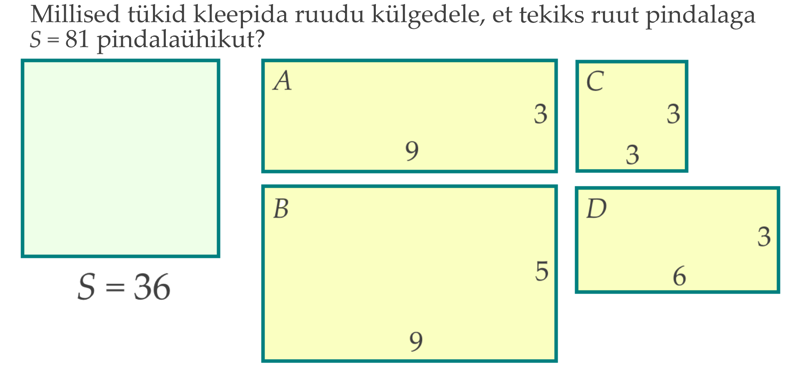
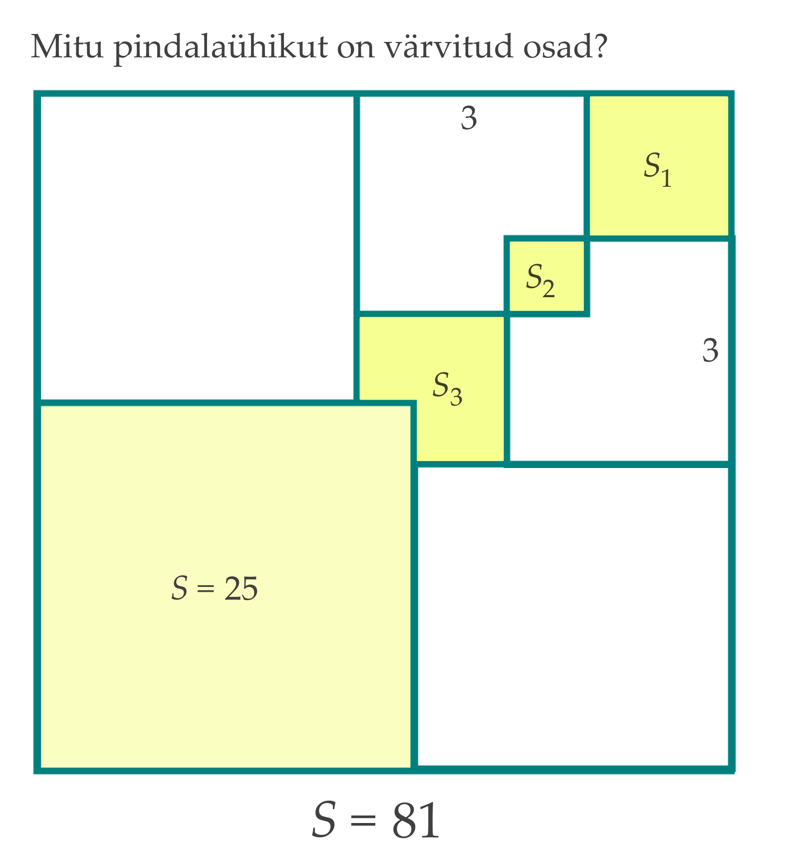
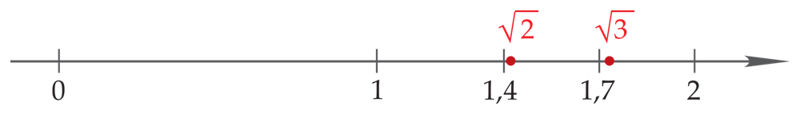Tunni ülesehitus

  1. Sissejuhatus, 7 min
  2. Töö õpiku tekstiga. Selgitused ja näited, 15 min
  3. Õpitu kinnistamine. ​Ülesannete lahendamine, 20 min
  4. Kokkuvõte, 3 min

Ettevalmistus

  • Valida sobiv sissejuhatav tegevus.
  • Valida näited.
  • Valida ülesanded iseseiseva tegevuse jaoks.
  • Otsustada, kas mängida tunni lõpus või mitte.
  • Otsustada, kas anda kodune töö ja milline anda.

Eelteadmised

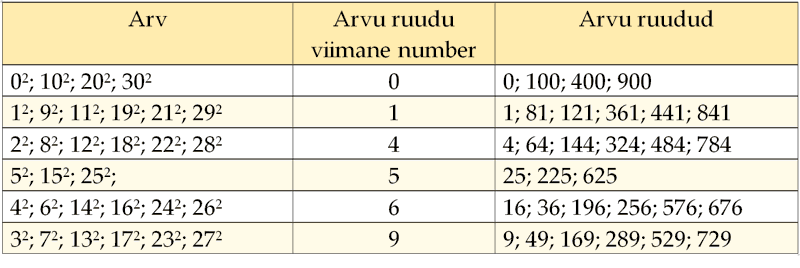
arvu ruutu võtmise tundmine

Eesmärgid

Õpilane

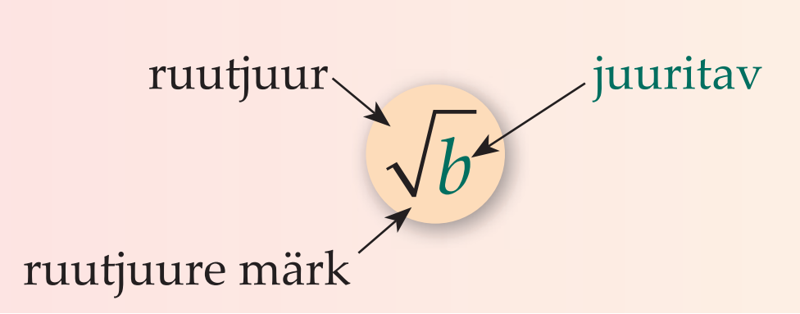
  • saab teada mis on arvu ruutjuur;
  • saab tuttavaks irratsionaalarvudega;
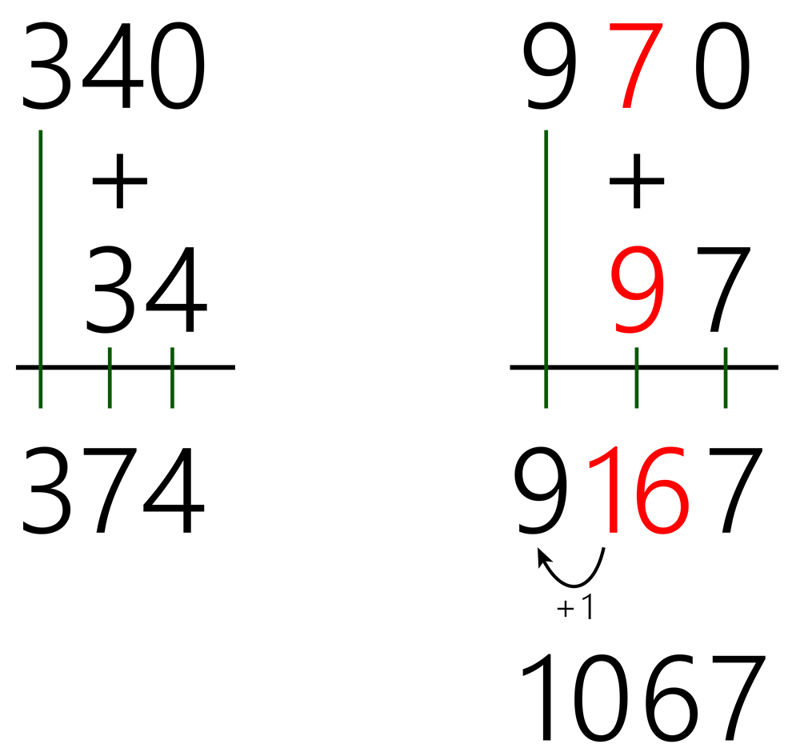
  • arvutab ruutjuuri sisaldava avaldise väärtust.

Seotud materjal

  • ​lk 12–16
  • ül 8–10
  • ptk 3.1
  • ülesanded

Märksõnad ja meetodid

  • arvu ruut, arvu ruutjuur, juurimine, tehtemärgid, pöördtehted, irratsionaalsed arvud
  • demonstratsioon, näitlikustamine, suunatud diskussioon, rakendused, tagasiside andmine, probleemi analüüs, ​iseseisev töö

Lõiming

eesti keel, tehnoloogia

Läbivad teemad

Tehnoloogia ja innovatsioon

Ще на цю тему
Інші дії

1. Sissejuhatus

  • Sissejuhatava teema valimine
    • Tehted pöördtehete rakendamiseks
  • Tean mida tean

7

Sissejuhatava teema valimine

Sissejuhatuseks piisab ühest tegevusest.

  • Hea on veelkord läbi töötada tehted ja nende pöördtehted. Slaidil on mõned avaldised, kus arvutamise välistamiseks on valitud suured arvud. Õpilastelt tasub põhjendamiseks oodata väidet, kus on kasutatud mõistet pöördtehe.
  • „Tean mida tean“ test keskendub ruudu külje täisarvuliste väärtuste äratundmisele. See on ettevalmistus arvu ruutudega tegelemiseks juurimistehte sooritamisel.

Sissejuhatavad ülesanded

Pöördtehted

Määra tehe a leidmiseks

  • 38^5+a=41
  • a-17 438=9^{11}
  • -15a=431
  • \frac{a}{29^3}=17^3

Tean mida tean

Tean mida tean Vastused

  1. Kui S = 4 ja S = 9
  2. Kui S = 26
  3. A ja D, saame ruudu küljega 9 pikkusühikut
  4. S1 = 22 = 4
    S2 =12 = 1
    S3 = 3, sest
    81 – 25  – 2·16 – 2·9 + 1 – 4 = 3​​​
Ще на цю тему
Інші дії

2. Teema selgitamine

  • Soovitused tööks õpiku tekstiga
    • Tehtemärk ja mõisted
    • Näited ruutjuurte kohta
    • Dünaamiline graafik arvu x, 0 < x < 2, ruutude ja ruutjuurte demonstreerimiseks
    • Soovitus tegevuse diferentseerimiseks, sh ülesanne ja vastus tabeli kujul
  • Distantsõppe juhised

8

Töö õpiku tekstiga

  • Enne ülesannete lahendamist on hea vaadelda kõikvõimalikke ruutjuure võtmisel esile tulevate vastuste võimalusi:
    1. ruutjuur on täisarv;
    2. ruutjuur on lõplik kümnendmurd;
    3. ruutjuur on lõpmatu kümnendmurd;
    4. ruutjuur on harilik murd.
  • Dünaamilise joonise abil saab vaadelda arvu ruutu ja ruutjuurt, kui arv on valitud 0 ja 2 vahelt.

Neile, kellele matemaatika meeldib

Seega ruutjuure võtmise põhipunkt laskub arvu ruutude ehk  ruutarvude äratundmisele. Korrutustabeli piires peaks see õpilastel selge olema. Mõtlemise paindlikuse huvides võiks töötada arvu ruutudega kuni 30-ni.

Õpilastelt tasub oodata tähelepanekut, et ruudu viimased numbrid võivad olla ainult: 0, 1, 4, 5, 6 või 9​.

Ühegi arvu ruut ei saa kunagi lõppeda 2, 3, 7 ega 8-ga.

Arvu ruudud

Koosta tabel arvude 0 kuni 30 ruutudest arvu ruudu viimaste numbrite kasvavas järjekorras.

Näiteks
212 ​arvu ruudu viimane number 1​ arvu ruut 441
82​ arvu ruudu viimane number 4​ arvu ruut 464
172 arvu ruudu viimane number 9​ arvu ruut 289
jne​

Reeglid ja näited

Mõisted

Ruutjuurt saab leida vaid
​ mittenegatiivsest arvust,
​sest ei leidu sellist arvu, mille ruut oleks negatiivne.

\sqrt{9}=3, sest 3^2=9

\sqrt{-9} puudub, sest ühegi arvu ruut pole –9

Ruutjuur on täisarv

\sqrt{25}=5, sest 5^2=25

\sqrt{289}=17, sest 17^2=289

\sqrt{63001}=251, sest 251^2=63001

\sqrt{34492129}=5873, sest 
​5873^2=34492129

Ruutjuur on lõplik kümnendmurd või harilik murd

\sqrt{0,01}=0,1, sest 0,1^2=0,01

\sqrt{2,56}=1,6, sest 1,6^2=2,56

\sqrt{\frac{4}{9}}=\frac{2}{3}, sest \left(\frac{2}{3}\right)^2=\frac{4}{9}

Ruutjuur on lõpmatu kümnendmurd

\sqrt{7}=2,6457513...

\sqrt{102}=10,0995049...

\sqrt{\frac{1}{10}}=0,3162277...

Kui täisarv on ruutarv, siis ruutjuur on täisarv.

Kui täisarv ei ole ruutarv, siis ruutjuur on alati lõpmatu kümnendmurd  ehk irratsionaalne arv.

Distantsõpe

ptk 3.1

Juhendada õpilast, millised peatüki osad on tingimata vaja läbi töötada ja millised võivad jääda õpilase valida.

Tagasiside saamiseks saata õpilasele ülesannete kogust lahendamiseks 2–3 jõukohast ülesannet.

Ще на цю тему
Інші дії

2. Süvendamine ja kinnistamine

  • Selgitused ja näpunäited
    • Arvtelg 
    • Tabel irratsionaalarvude paiknemise kohta
    • Arvuhulkade joonis.
  • Liikumispaus

7

Selgitused ja näpunäited

  • Tutvudes irratsionaalarvudega on hea, kui õpilased saavad  märkida arvteljele 0 < x < 4 arvude \sqrt{2},\ \sqrt{3},\ ...,\ \sqrt{10} ligikaudset paiknemiskohta. Seda võib organiseerida ka tabelina. Oluline on, et õpilastel tekiks ülevaade.
  • Kui on kohane, võib õpilastel paluda tabeli täitmist jätkata mõnda lisatingimust arvestades, näiteks nii:„Märgi järgmisele reale ruutjuur täisarvust, mis on küll irratsionaalne aga arvule 6 võimalikult lähedal.“ vms 

Koos lahendatav ülesanne

Ratsionaalarvude hulk ℚ koos irratsionaalarvude hulgaga I moodustavad reaalarvude hulga ℝ. Reaalarvude hulk ℝ sisaldab endas kõiki varemõpitud arvuhulki ℕ, ℤ, ℚ.

Liikumispaus

1 minut

Ще на цю тему
Інші дії

3. Õpilaste iseseisev tegevus

  • Harjutuste loetelu
  • Ülesannete loetelu
  • Valitud ülesannete lahendusi
    • Õpiku ül 46
    • Õpiku ül 47

20

Valida tundi õpilastele jõukohased ülesanded. Leida võimalus, et õpilased saaksid oma lahendusi kaasõpilastele esitleda.

Harjutused

  • ül 23–28
  • ül 29 on jäetud kodutöö üheks variandiks
  • ptk 3.1 ülesannete kogust „Puuduvad juuremärgid“

Ülesanded

  • ül 30–42
  • ül 43 on jäetud kodutöö üheks variandiks
  • ül 44–48
  • ptk 3.1 ülesannete kogust „Pindvõrdsed ristkülik ja ring 2“

Valitud ülesannete lahendusi

Õpiku ül 46

Võrdkülgse kolmnurga pindala saab arvutada valemiga S=\frac{a^2\sqrt{3}}{4}.

  • Kui S=\sqrt{3}, siis \frac{a^2\sqrt{3}}{4}=\sqrt{3} ja
    a^2=4,\ a=2​
  • Kui S=81\sqrt{3}, siis \frac{a^2\sqrt{3}}{4}=81\sqrt{3} ja
    a^2=324,\ a=18​
Õpiku ül 47

\sqrt{a-6}

Kui a-6=0, siis a=6 korral on juure väärtus 0,
​seega a\ge6, et juure alla tuleks mittenegatiivne arv.

\sqrt{3x+15}
Kui 3x+15=0, siis x=-5 korral on juure väärtus 0,
seega x\ge-5, ​​​et juure alla tuleks mittenegatiivne arv.

Ще на цю тему
Інші дії

Lisamaterjal

Peastarvutamine 1. Korrutamine 11‑ga​

Kahekohalise arvu korrutamise 11-ga saame asendada liitmisega.

Teame, et 11 = 10 + 1 ning 11 · n = (10 + 1) · n = 10 · n + n

Veendu 11 · 23; 11 · 54; 11 · 75 ja 11· 92.

Leia strateegia 22-ga korrutamiseks, teades, et 22 = 2 · 11

11 · 34 ja 11 · 97 korrutamise asendamine peastarvutamisel liitmisega
Mõtlemise paindlikkuse arendamine
Ще на цю тему
Інші дії

Kodutöö ja tunni kirjeldus

Kodutöö

≈ 10–20 min. Võimalik on valida igale õpilasele üks jõukohane ülesanne nende hulgast.

Kodutöö

Õpitu kordamine

Õpiku ül 29

Kodutöö

Õpitu rakendamine uues olukorras

Õpiku ül 43

Tunni kirjeldus

Ruutjuur ja irratsionaalarvud

Õpiku ptk 2.1
​TV ül 8–10
​Opiqu ptk 3.1

Ще на цю тему
Інші дії