Variatsioonid ja kombinatsioonid

Näide 1.

Mitmel erineval viisil saavad ühe klassi 25 õpilasest siseneda viis esimest oma klassiruumi, kui vahetunnis olid nad kõik koridoris?

Esmalt peab olema selge, millal loetakse klassi sisenemisi erinevateks. Ilmselt tuleb viie esimese õpilase sisenemisi klassi lugeda erinevateks, kui kas või üks õpilane 5 esimese seas on vahetunud või kui sisenemisel kas või kaks vahetavad kohad (näiteks üks möödub teisest enne sisenemist). Matemaatilisest seisukohast loetakse need ühendid (5 esimest sisenejat) erinevaks, kui kasvõi üks element (õpilane) asendub teisega või kui elementide järjestus ühendites on erinev. Edasi arutleme järgmiselt. Erinevaid võimalusi esimese õpilase sisenemiseks on 25. Kui esimene õpilane on juba klassis, on teise jaoks 24 võimalust. Analoogiliselt kolmanda jaoks 23, neljanda jaoks 22 ja viienda jaoks 21 võimalust. Seega on kombinatoorika korrutamislause (sisenema peab nii esimene, teine, ... kui ka viies õpilane) põhjal viie esimese õpilase klassi sisenemiseks 25 ⋅ 24 ⋅ 23 ⋅ 22 ⋅ 21 = 6 375 600 erinevat võimalust.

Vaatleme analoogilist situatsiooni üldjuhul. Olgu elemente (objekte) n ja neist tuleb moodustada k-elemendilisi ühendeid, mis erinevad üksteisest kas elementide või nende järjestuse poolest. Mitmel erineval viisil saab neid ühendeid n elemendist k-kaupa moodustada? Et 1. elemendi valikuks on võimalusi n, 2. valikuks võimalusi n – 1, 3. valikuks võimalusi n – 2 jne ning lõpuks k-nda valikuks võimalusi n – (k – 1) ehk n – k + 1, siis erinevaid ühendeid n elemendist k-kaupa saab moodustada

$\underset{k tegurit}{\underset{⏟}{n \cdot (n - 1) \cdot (n - 2) \cdot \dots \cdot (n - k + 1)}}$ .

Näide 2.

Matkale läheb 10-liikmeline seltskond. Nende hulgast valitakse matkagrupi toimkond, kuhu kuuluvad grupivanem, peakokk ja päevikupidaja. Mitu erinevat toimkonda saaks nende 10 inimese seast valida?

Toimkonnad loetakse erinevateks, kui sinna kuulub kas või üks uus inimene või kui toimkonnas jaotatakse ametid erinevalt (elementide järjestus). Seega on tegemist üldjuhul kirjeldatud ühenditega ning erinevate toimkondade võimalik arv on 10 ⋅ 9 ⋅ 8 = 720.

Eespool kirjeldatud ühendeid, mis erinevad üksteisest kas elementide või nende järjestuste poolest ühendis, nimetatakse variatsioonideks. Variatsioone defineeritakse tavaliselt järgmiselt.

Variatsioonideks n elemendist k-kaupa (k ≤ n) nimetatakse n-elemendilise hulga kõigi k-elemendiliste osahulkade elementide erinevaid järjestusi.

Näide 3.

Hulgal {a, b, c, d, e} on kolmeelemendilisi osahulki 10: {a, b, c}, {a, b, d}, {a, b, e}, {a, c, d}, {a, c, e}, {a, d, e}, {b, c, d}, {b, c, e}, {b, d, e}, {c, d, e}. Need osahulgad erinevad üksteisest vaid elementide poolest. Kui neist i g a s osahulgas teha kõikvõimalikud kolme elemendi ümberpaigutused, saamegi variatsioonid 5 elemendist 3-kaupa. Esimese osahulga elementidest saame 6 erinevat järjestust: abc, acb, bac, bca, cab,cba. Nii iga kümne osahulga korral. Kokku saame seega viiest antud elemendist (a, b, c, d, e) kolmekaupa variatsioone 10 · 6 = 60. Sama tulemuse oleksime saanud ka eespool leitud avaldise $\underset{k tegurit}{\underset{⏟}{n \cdot (n - 1) \cdot (n - 2) \cdot \dots \cdot (n - k + 1)}}$ abil: 5 · 4 · 3 = 60.

Variatsioonide arvu n elemendist k-kaupa tähistatakse sümboliga V_n^k või A_n^k. Seega

V_{n}^{k}

= $n \cdot (n - 1) \cdot (n - 2) \cdot \dots \cdot (n - k + 1)$ = $\frac{n!}{(n - k)!}$

Seni vaatlesime ühendeid, mida saab moodustada n elemendist k-kaupa, kusjuures ühendid loetakse erinevateks, kui nad erinevad üksteisest vähemalt ühe elemendi poolest või elementide järjestuse poolest ühendis.

Kui vaadelda aga ühendeid, mida moodustatakse samuti n elemendist k-kaupa, kuid ühendid loetakse erinevateks siis, kui nad erinevad üksteisest vaid elementide poolest, saadakse nn kombinatsioonid. Kombinatsioonide korral ei ole elementide järjestus tähtis. Kombinatsioone defineeritakse üldjuhul järgmiselt.

Kombinatsioonideks n elemendist k-kaupa (k ≤ n) nimetatakse n-elemendilise hulga k-elemendilisi osahulki.

Näide 4.

Spordikooli kahekümnest tütarlapsest on tarvis moodustada 6-liikmeline võrkpallivõistkond. Mitu erinevat võistkonda saaks moodustada?

Moodustame esialgu kõikvõimalikud võistkonnad, kus peale isikute on tähtis ka nende järjestus. Selliseid erinevaid võistkondi saaks 20 ⋅ 19 ⋅ 18 ⋅ 17 ⋅ 16 ⋅ 15. Kuna aga järjestus ei ole oluline, väheneb leitud võistkondade arv 6! korda, sest samu tütarlapsi sisaldavaid esialgseid võistkondi on samapalju kui kuue tütarlapse erinevaid võimalikke järjestusi (sisuliselt permutatsioone, mida on P_6=6!). Seega on meid huvitav võistkondade arv(20 · 19 · 18 · 16 · 15) : 6! = 38 760.

Kombinatsioonide arvu n elemendist k-kaupa tähistatakse sümboliga C_n^k või sümboliga

(_{k}^{n})

, mida loetakse n üle k. Korrates näites 4 kasutatud mõttekäiku üldjuhul, saame, et

C_n^k=\frac{n\cdot\left(n-1\right)\cdot\left(n-2\right)\cdot...\cdot\left(n-k+1\right)}{k!}Laiendades murdu teguriga (n – k)! onC_n^k=\frac{n\cdot\left(n-1\right)\cdot\left(n-2\right)\cdot...\cdot\left(n-k+1\right)\cdot\left(n-k\right)!}{k!\cdot\left(n-k\right)!}ehk

C_{n}^{k} = \frac{n!}{k! (n - k)!}

Kehtib ka seos

$C_{n}^{k} = C_{n}^{n - k}$ .

mille õigsus ilmneb kohe, kui kirjutada välja C_n^k ja C_n^{n-k} avaldised. Näiteks C_7^5=C_7^2=21.Üheelemendilise hulga (n = 1), näiteks hulga \left\{\Delta\right\} elementidest saab moodustada üheelemendilisi (k = 1) osahulki (kombinatsioone) vaid ühe. Seega C_1^1=1. Et sama tulemuse saaksime valemist C_n^k=\frac{n!}{k!\left(n-k\right)!}, peab 1=\frac{1!}{1!\cdot\left(1-1\right)!} ehk 1=\frac{1}{0!}, mis on aga võimalik vaid siis, kui defineerida

0! = 1.

Definitsioonide 1! = 1 ja 0! = 1 tõttu saab nüüd ka sümbol C_n^0 tähenduse. Kombinatsioonide definitsiooni kohaselt on see n-elemendilise hulga null-elemendiliste osahulkade (sisuliselt tühja hulga kui osahulga) arv. Selliseid osahulki \left\{\ \right\}=\varnothing on igal hulgal vaid üks \left(C_n^0=1\right).Avaldise C_n^k väärtused esinevad varjatult juba põhikoolis õpitud valemites:\left(a+b\right)^1=a+b ehk \left(a+b\right)^1=C_1^0a+C_1^1b\left(a+b\right)^2=a^2+2ab+b^2 ehk \left(a+b\right)^2=C_2^0a^2+C_2^1ab+C_2^2b^2\left(a+b\right)^3=a^3+3a^2b+3ab^2+b^3 ehk \left(a+b\right)^3=C_3^0a^3+C_3^1a^2b+C_3^2ab^2+C_3^3b^3Nende valemite üldistuseks on nn Newtoni binoomvalem

{(a + b)}^{n} = C_{n}^{0} a^{n} + C_{n}^{1} a^{n - 1} b + C_{n}^{2} a^{n - 2} b^{2} + \dots + C_{n}^{n - 1} a b^{n - 1} + C_{n}^{n} b^{n}

Siin esinevaid kordajaid C_n^0, C_n^1, C_n^2, … C_n^{n-1}, C_n^n nimetatakse binoomkordajateks.

Võttes binoomvalemis a = b = 1, saame, et binoomkordajate summa

C_{n}^{0} + C_{n}^{1} + C_{n}^{2} + \dots + C_{n}^{n} = 2^{n}

Siit järeldub: n-elemendilise hulga kõigi osahulkade arv (kaasa arvatud tühihulk) on 2^n.

Paigutades binoomkordajad alljärgneval viisil, saame nn Pascali kolmnurga

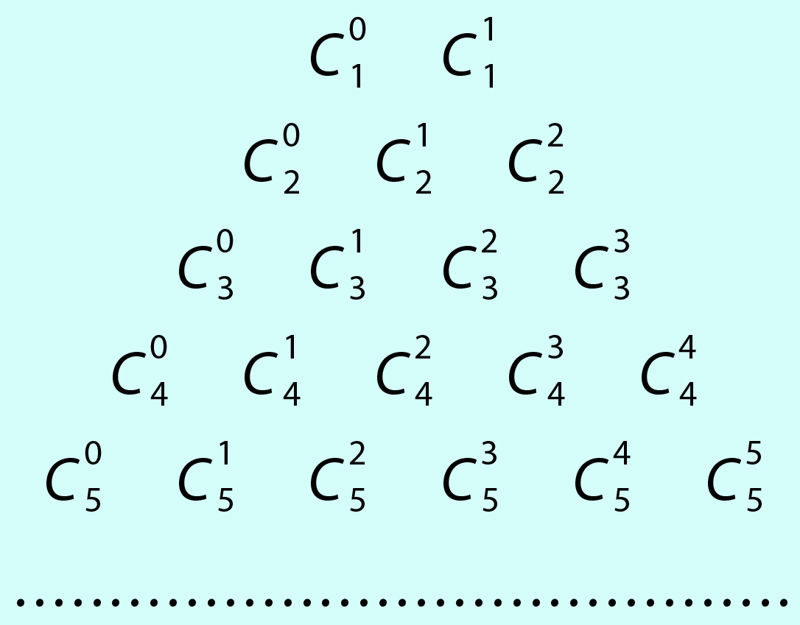Kui binoomkordajad arvutada, on Pascali kolmnurk järgmine:

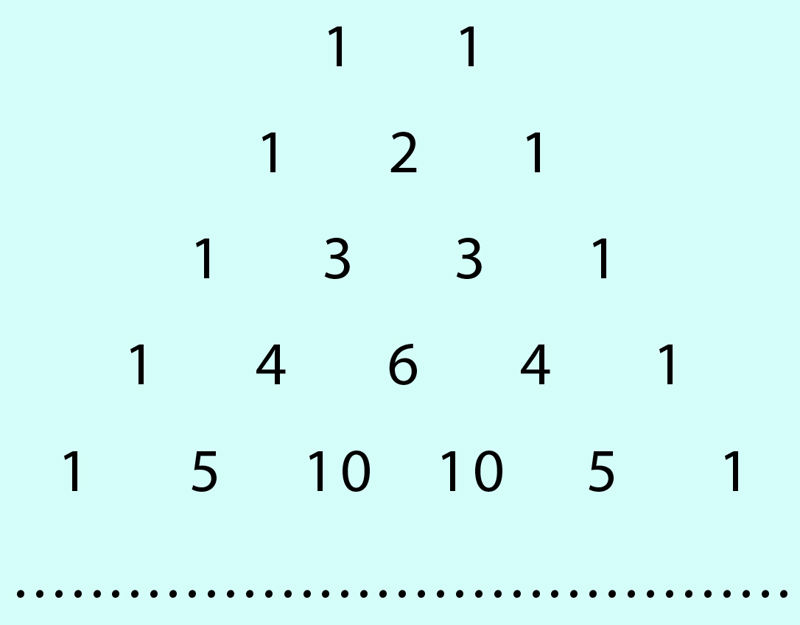Nuputage, kuidas saada eelmise rea põhjal järgmist rida! Vajadusel vt ülesannet 55.

Näide 5.

Kirjutame välja binoomvalemi (a + b)⁵.

Et n = 5, saame binoomkordajad Pascali kolmnurga viiendast reast ja

(a + b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵.

Avaldise (a – b)ⁿ esitamiseks summana kirjutame vahe (a – b) kujul [a + (–b)] ning rakendame siis Newtoni binoomvalemit.

Näide 6.

Kirjutame välja (2x – x²)⁴. Binoomkordajad saame Pascali kolmnurga neljandast reast. Nüüd

(2x – x²)⁴ = [2x + (–x²)]⁴ =

= (2x)⁴ + 4(2x)³(–x²) + 6(2x)²(–x²)² + 4(2x)¹(–x²)³ + (–x²)⁴ =

= 16x⁴ – 4 · 8 · x³ · x² + 6 · 4 · x² · x⁴ – 8 · x · x⁶ + x⁸ =

= 16x⁴ – 32x⁵ + 24x⁶ – 8x⁷ + x⁸.

Seotud sisu

Ülesanded A

Ülesanne 32. Auhindade jaotumine

Vastus. Auhinnad võivad jaotuda võistkondade vahel erineval viisil.

Ülesanne 33. Õpikute mahalaadimine

Vastus. See nimekiri võis tekkida erinevas järjestuses.

Ülesanne 34. Tunniplaan

Vastus. Meil on tunniplaanis õppeainet.

Mitmel erineval viisil saab nendest ainetest koostada ühe päeva tunniplaani, kui päevas on 6 erinevat tundi?

Vastus. Nendest ainetest saab koostada erinevat ühe päeva tunniplaani.

Ülesanne 35. Koosoleku juhataja ja protokollija valimine

Vastus. Koosoleku juhataja ja protokollija valimiseks on erinevat viisi.

Kui palju on võimalusi siis, kui ei ole oluline, kumb juhatab koosolekut, kumb protokollib?

Vastus. Kui ei ole oluline, kumb juhatab koosolekut, kumb protokollib, siis on võimalusi .

Ülesanne 36. Ülesannete koostamine

Vastus. Saadi ülesannet. Nende seas korduvaid.

Ülesanne 37. Kombinatsioonid

C_{509}^{507} =

C_8^5\ :\ C_8^3 =

C_{10}^5\left(C_7^2-C_9^2\right) =

18\cdot17\cdot16\ :\ C_{18}^6 =

Ülesanne 38. Testi küsimustele vastamine

Vastus. Seda saab teha erineval viisil.

Ülesanne 39. Matemaatikatunnis istumine

Ülesanne 40. Sirged

8 punkti

Vastus. 8 punktiga on määratud erinevat sirget.
20 punkti

Vastus. 20 punktiga on määratud erinevat sirget.
n punkti

Vastus. n punktiga on määratud erinevat sirget.

Ülesanne 41. Sirged ja kolmnurgad

Mitu erinevat sirget on nende punktidega määratud?
Vastus. Nende punktidega on määratud erinevat sirget.
Tehke vastav joonis ja kirjutage need sirged välja.
Mitu kolmnurka on nende punktidega määratud? Kirjutage need.
Vastus. Nende punktidega on määratud kolmnurka: .

Ülesanne 42. Loterii

Vastus. Selleks on võimalust.

Ülesanne 43. Võistkondade moodustamine

Vastus. Võistkondi saab moodustada erineval viisil.

Ülesanne 44. Laudade juurde istumine

Vastus. Nad saavad laudade juurde istuda erineval viisil.

Ülesanne 45. Millal kehtib võrdus?

C_9^3=C_9^k?

Vastus. Võrdus kehtib kui k = ja kui k = .

Ülesanne 46. Sünnipäevakingi ostmine

Vastus. Tal on erinevat valikuvõimalust.

Ülesanne 47. Võistkonna valimine

Vastus. See laudkond saab oma võistkonda valida erineval viisil.

Ülesanne 48. Ruudukeste värvimine

8 roosaks ja 8 roheliseks?

Vastus. Nii saab värvida erineval viisil.
2 punaseks ja ülejäänud mustaks?

Vastus. Nii saab värvida erineval viisil.
2 punaseks, 4 siniseks ja 10 pruuniks?

Vastus. Nii saab värvida erineval viisil.

Ülesanne 49. Ruumi valgustamine

Vastus. Ruumi saab nende lampidega valgustada erineval viisil.

Kui palju on võimalusi, kui süüdata tohib kõige rohkem 5 lampi?

Vastus. Siis on erinevat võimalust ruumi valgustamiseks.

Ülesanne 50. Kokkusaamised sõpradega

Vastus. Selleks kulus nädalavahetust.

Ülesanne 51. Sõprade juurde minemine

Joon 1.2

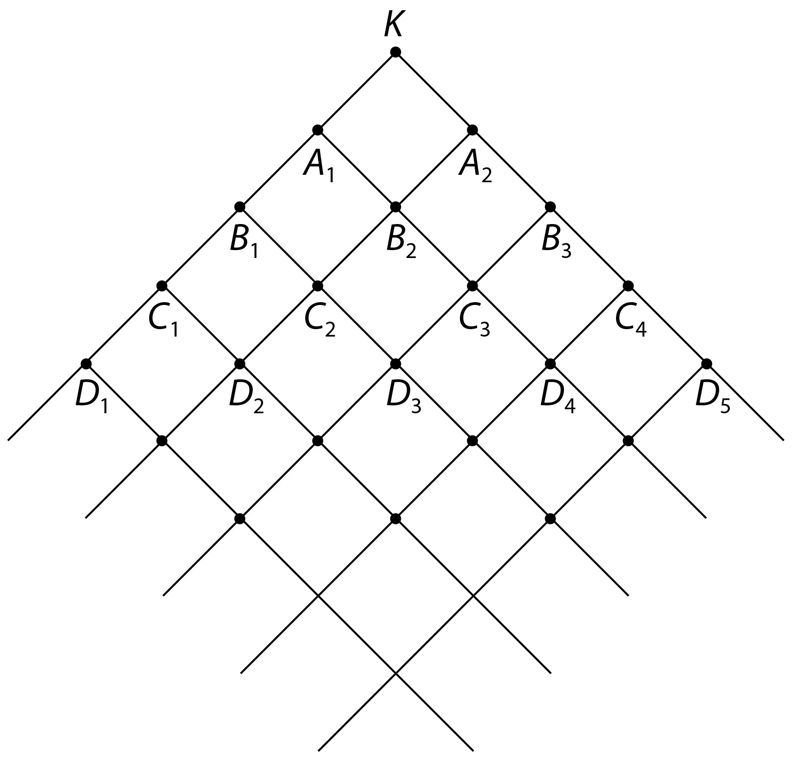
Vastus. D₁ juurde viisil, D₂ juurde viisil, D₃ juurde viisil, D₄ juurde viisil ja D₅ juurde viisil.

Milline tee on neist pikim?

Seotud sisu

Ülesanded B

Ülesanne 52. Variatsioonid

V_9^2 =

V_{30}^1 =

\left(V_8^3+V_7^2\right)\ :\ V_9^4 =

V_6^6\cdot V_3^2 =

Ülesanne 53. Variatsioonid

V_{n+3}^4 =

V_{n+1}^{n-1} =

\left(V_n^5+V_n^4\right)\ :\ V_n^3 =

V_{n+5}^n\ :\ V_{n+4}^{n-2} =

Ülesanne 54. Variatsioonid, kombinatsioonid ja permutatsioonid

V_{17}^5\ :\ C_5^2\ :\ P_3 =

C_5^3\cdot C_5^4\ :\ V_5^1 =

V_{13}^3\cdot\frac{P_7}{12P_6} =

\frac{V_n^4P_{n-4}}{C_n^1} =

Ülesanne 55. Tõestamine

Pascali kolmnurga ridade väljakirjutamine arvulisel kujul tugineb seosele C_n^{m-1}+C_n^m=C_{n+1}^m. Tõestage see.

Ülesanne 56. Laudade juurde istumine

Vastus. Nad saavad laudade juurde istuda erineval viisil.

Ülesanne 57. Maleturniir

Vastus. Turniirist osavõtjaid oli .

Ülesanne 58. Võrkpalli segavõistkond

4 noormeest ja 2 neiut?

Vastus. erineval viisil.
vähemalt 2 neiut?

Vastus. erineval viisil.

Ülesanne 59. Kuulide võtmine

Vastus. Selleks on võimalust.

Ülesanne 60. Puuviljade võtmine

Vastus. Puuvilju saab võtta erineval viisil.

Ülesanne 61. Nuppude paigutamine

Mitmel erineval viisil saab neisse ruutudesse paigutada 25 täiesti ühesugust nuppu (s.t nuppude järjestust ei arvestata)?

Vastus. erineval viisil.
Mitmel erineval viisil saab neisse ruutudesse paigutada 25 erivärvilist nuppu?

Vastus. erineval viisil.

Märkus: vajadusel võib arvutamiseks kasutada Google’i või arvuti kalkulaatorit.

Ülesanne 62. Newtoni binoomvalem

\left(a+b\right)^6 =

\left(x+1\right)^4 =

\left(2c+3\right)^5 =

\left(a-b\right)^5 =

\left(3a^2-2a\right)^4 =

Ülesanne 63. Variatsioonid

Ülesanne 64. Võrrandi lahendamine

V_x^3=56x

x =

Seotud sisu

Opiqus edenemine

	Tööd
	Peatükk on läbi töötatud

Variatsioonid ja kombinatsioonid

Seotud sisu

Ülesanded A

Ülesanne 32. Auhindade jaotumine

Ülesanne 33. Õpikute maha­laadimine

Ülesanne 34. Tunniplaan

Ülesanne 35. Koos­oleku juhataja ja protokollija valimine

Ülesanne 36. Ülesannete koostamine

Ülesanne 37. Kombinatsioonid

Ülesanne 38. Testi küsimustele vastamine

Ülesanne 39. Matemaatika­tunnis istumine

Ülesanne 40. Sirged

Ülesanne 41. Sirged ja kolm­nurgad

Ülesanne 42. Loterii

Ülesanne 43. Võist­kondade moodustamine

Ülesanne 44. Laudade juurde istumine

Ülesanne 45. Millal kehtib võrdus?

Ülesanne 46. Sünni­päeva­kingi ostmine

Ülesanne 47. Võist­konna valimine

Ülesanne 48. Ruudukeste värvimine

Ülesanne 49. Ruumi valgustamine

Ülesanne 50. Kokku­saamised sõpradega

Ülesanne 51. Sõprade juurde minemine

Seotud sisu

Ülesanded B

Ülesanne 52. Variatsioonid

Ülesanne 53. Variatsioonid

Ülesanne 54. Variatsioonid, kombinatsioonid ja permutatsioonid

Ülesanne 55. Tõestamine

Ülesanne 56. Laudade juurde istumine

Ülesanne 57. Male­turniir

Ülesanne 58. Võrk­palli sega­võistkond

Ülesanne 59. Kuulide võtmine

Ülesanne 60. Puu­viljade võtmine

Ülesanne 61. Nuppude paigutamine

Ülesanne 62. Newtoni binoom­valem

Ülesanne 63. Variatsioonid

Ülesanne 64. Võrrandi lahendamine

Seotud sisu

Lisa materjali

Lisatavad failid

Teata veast

Teata siia ainult Opiqu veast. Palun kirjelda viga nii täpselt kui võimalik.

Kui ootad Opiqu meeskonnalt vastust, lisa oma kontaktandmed (e-post, telefon).

Tee linnuke, et aidata meil spämmiga võidelda

Opiq kasutab küpsiseid

Ülesanne 33. Õpikute mahalaadimine

Ülesanne 35. Koosoleku juhataja ja protokollija valimine

Ülesanne 39. Matemaatikatunnis istumine

Ülesanne 41. Sirged ja kolmnurgad

Ülesanne 43. Võistkondade moodustamine

Ülesanne 46. Sünnipäevakingi ostmine

Ülesanne 47. Võistkonna valimine

Ülesanne 50. Kokkusaamised sõpradega

Ülesanne 57. Maleturniir

Ülesanne 58. Võrkpalli segavõistkond

Ülesanne 60. Puuviljade võtmine

Ülesanne 62. Newtoni binoomvalem