Õhk avaldab rõhku
Ilmateates on lisaks õhutemperatuurile alati üheks kindlaks suuruseks õhurõhk. Eelmises õppetükis me nägime, et vedelik avaldab rõhku, mis sõltub vedelikukihi massist ja sellega seotud raskusjõust. Maad ümbritseb õhukiht ehk atmosfäär. Õhul on samuti teatav mass ja sellele mõjub raskusjõud. Seetõttu ei ole üllatav, et ka õhk avaldab maapinnale rõhku. Seda rõhku me nimetame õhurõhuks. Õhurõhk ei mõju mitte ainult Maa pinnale, vaid kõikidele Maal olevatele kehadele, sealhulgas ka inimesele. Õhurõhu jaoks meil lihtsat valemit tuletada ei õnnestu, sest õhu tihedus kõrgusega väheneb ja seetõttu on õhu massi ja rõhu arvutamine keeruline. Küll aga saame õhurõhku mõõta ja selle kaudu hinnata õhu massi, mis seda rõhku põhjustab. Samuti võime öelda, et kõrgusega õhurõhk väheneb, sest ülespoole jääva õhu hulk on väiksem.
Järgnevalt räägime sellest, kuidas omal ajal õhurõhk avastati ja katseliselt tõestati. Nagu peatüki sissejuhatavas osas kirjas, tekkis probleem kaevuga, mille sügavus oli suurem kui kümme meetrit, sest sealt ei õnnestunud pumbaga vett kätte saada, vesi tõusis pumbatorus kuni 10,3 m kõrguseni.
Mõtteline katse Rõuge Suurjärvel
Füüsikatunnis rääkis õpetaja õhurõhust. Tunni alguseks oli ta lauale pannud akvaariumi värvilise veega. Üks õpilastest pidi kummulipööratud klaasiga vett tõstma. Klaas tuli asetada vette, nii et see täitus veega, siis ümber pöörata ja veest välja tõsta. Katse on huvitav, sest seni, kuni klaasi alumine ots on vees ja klaasi õhku ei pääse, tõuseb klaasis olev vesi akvaariumi veepinnast kõrgemale. Samal põhimõttel me „tõstame” pumbaga kaevust vett.

Siis aga küsis õpetaja: „Mis juhtub, kui tõsta vett toruga, mis on näiteks 35 m pikk?”
Põhimõtteliselt saaks sellise katse teha Rõuge Suurjärvel.

Katse algaks nii, et toru on surutud üleni vette. Veega täitunud toru ülemine ots suletakse ja hakatakse toru veest välja tõstma.
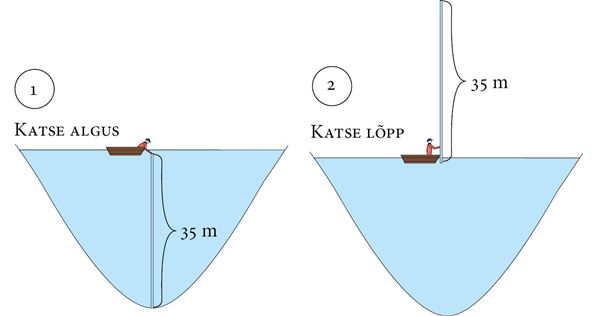
Õpilased arvasid, et saab küll nii pika toruga vett tõsta. Kui sai vett tõsta klaasiga, miks siis ei saaks seda teha pika toruga. Järgnevalt näeme, et see oletus ei ole õige. Toru tõstmisel saab vesi torus tõusta samuti ainult 10,3 m kõrgusele, pikemast torust ei oleks vee tõstmisel mingit kasu.
Torricelli katse
Kaevuprobleemi lahendas Galilei õpilane Torricelli, kes oletas, et põhjuseks, miks vesi torus tõuseb, on õhurõhk. Ta tuli geniaalsele ideele teha katse elavhõbedaga. Kui vesi kaevutorus tõuseb 10,3 meetri kõrgusele, siis elavhõbeda sammas peaks tõusma 76 cm kõrgusele. On ju elavhõbeda tihedus vee omast 13,6 korda suurem ja seetõttu avaldab 10,3 m kõrgune veesammas sama suurt rõhku kui 13,6 korda lühem ehk 76 cm kõrgune elavhõbedasammas.
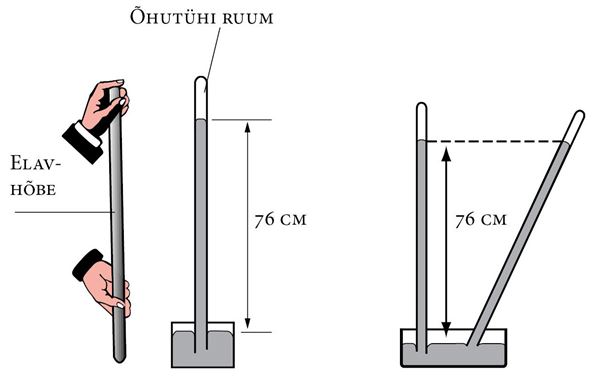
Torricelli võttis umbes 1 m pikkuse ühest otsast kinnise klaastoru ja täitis selle elavhõbedaga. Hoides toru lahtist otsa suletuna, pööras ta toru ümber ja asetas elavhõbedaga anumasse. Lastes toru otsa lahti, voolas osa elavhõbedat torust välja, torusse jäi umbes 76 cm kõrgune elavhõbedasammas.
Huvitav oli see, et kui toru kallutada, tuli torusse elavhõbedat juurde, aga alati niipalju, et samba kõrgus anumas olevast elavhõbeda nivoost jäi samaks, ikka 76 cm.
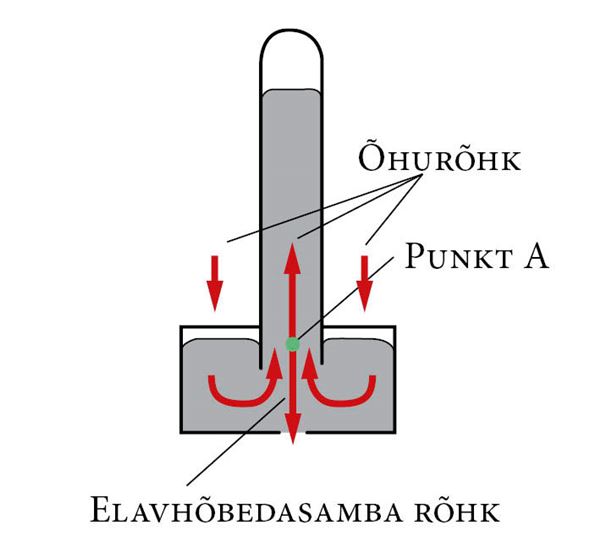
Sellest katsest järeldaski Torricelli, et elavhõbedasammast hoiab üleval õhurõhk. Tema mõttekäik oli järgmine: kui anumas oleva elavhõbeda pinnale mõjub mingi suurusega õhurõhk, siis sama suur rõhk peab olema ka samal kõrgusel klaastorus (joonisel punktis A). Seda rõhku tasakaalustab klaastorus oleva elavhõbedasamba rõhk.
Seda, et tõepoolest on tegemist õhurõhuga, kinnitasid Pascali hilisemad katsed, mis näitasid ka seda, et kõrgemal mägedes elavhõbedasamba kõrgus väheneb. See on igati loogiline, sest kõrgemal on ülespoole jääv õhukiht väiksem ja sellest tingituna on väiksem ka õhurõhk.
Torricelli katse lahendas ka kaevuprobleemi, sest kui elavhõbedasammas tõuseb klaastorus õhurõhu toimel 76 cm kõrgusele, siis analoogilises torus olev veesammas saaks veega kaevus tõusta 10,3 m kõrgusele. See aga tähendab, et sügavamast kaevust vett pumbata ei saa.
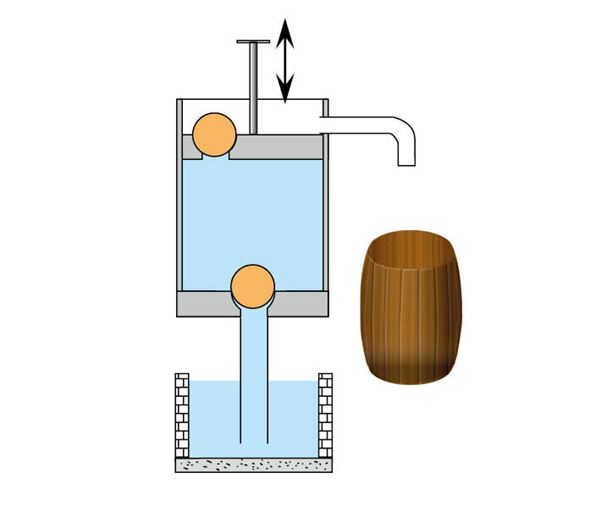
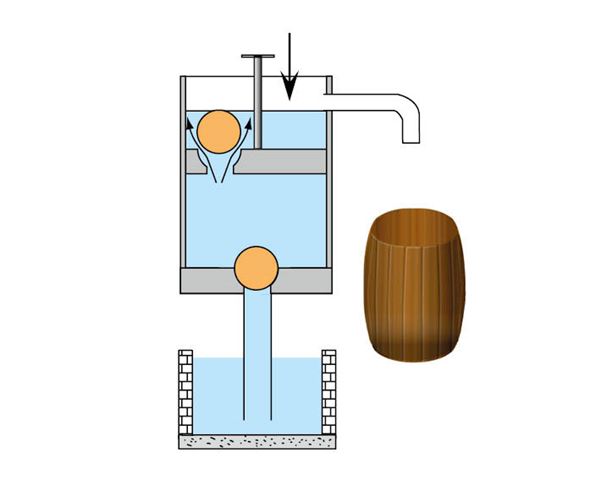
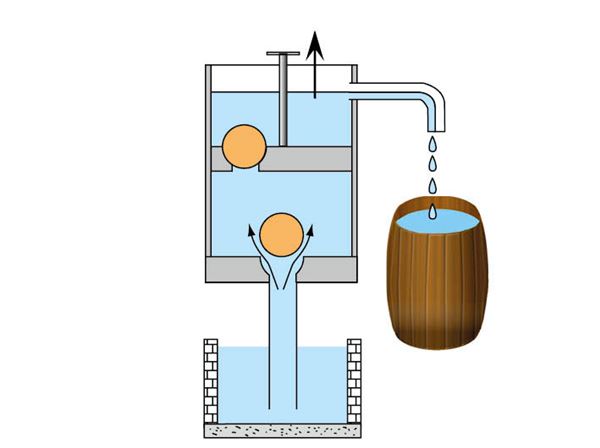
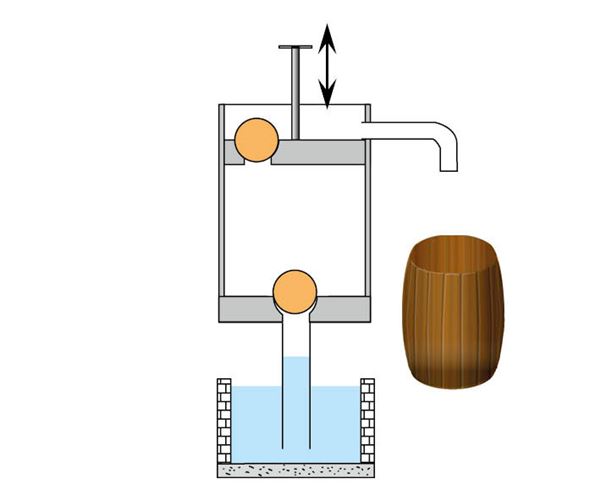
Kolbpump
Kaevupumpasid on kahesuguseid. Kaevus, mille vee tase on maapinnast 7–8 m allpool, saab pumba panna maapinna kõrgusele. Sügavamates kaevudes pannakse pump kaevus vette. Käsitleme esimest juhtumit kolbpumba näitel.
Õhurõhu ühikud
Õhurõhku saab mõõta elavhõbedasamba kõrguse järgi. Selle järgi kujunes välja aastasadu kasutusel olnud rõhuühik 1 mmHg (üks millimeeter elavhõbedasammast). Õhurõhk pole püsiva väärtusega, vaid varieerub, sõltudes geograafilisest asukohast ja ilmastikutingimustest. Õhurõhu mõõtmised näitavad, et 45 laiuskraadil on 0 °C juures keskmiseks õhurõhuks merepinna kõrgusel 760 mmHg. Seetõttu on õhurõhk 760 mmHg võetud kokkuleppeliselt õhurõhu hindamisel aluseks ja rõhku 760 mmHg nimetatakse seetõttu normaalrõhuks.
Õhurõhk on üks olulisemaid ilma kujundajaid. Kõrgema rõhu korral on tegemist ilusa ja enamasti selge ilmaga, madalama rõhu korral aga pilves ja vihmase ilmaga. Õhurõhk aga kujundab tuult, sest õhk liigub kõrgema õhurõhuga piirkonnast madalama õhurõhuga piirkonda.
Tänapäeval on rõhuühikuks 1 Pa. Kasutades vedelikusamba rõhu valemit, arvutame normaalrõhule vastava 760 mm kõrguse elavhõbeda samba rõhu põhiühikutes paskalites
p = ρgh = 13 600 · 9,8 · 0,76 m = 101 300 Pa.
(Siin me kasutasime arvutamisel g täpsemat väärtust g = 9,8 ).
Õhurõhu korral kasutatakse peamise ühikuna hektopaskalit (1 hPa = 100 Pa). Seega on normaalrõhk 760 mmHg hektopaskalites 1013 hPa. Meie ilmateadetes antakse õhurõhku enamasti mõlemates ühikutes.
Normaalrõhk on 1013 hPa ehk 760 mmHg.
Õhurõhu sõltuvus kõrgusest
Ilmateates antakse õhurõhk merepinna kõrgusel. Kõrgemal on õhurõhk väiksem. Kui merepinnast kõrgemale tõusta, väheneb õhurõhk iga meetri kohta umbes 12,5 Pa. Kui näiteks maakoht on merepinnast 60 m kõrgusel, on seal õhurõhk 60 · 12,5 Pa = 750 Pa võrra väiksem.
Õhu tihedus kahaneb kõrgusega üsna kiiresti ja sellega koos ka õhurõhk. Nii on 5 km kõrgusel õhurõhk normaalsest pea kaks korda väiksem (umbes 540 hPa), 10 km kõrgusel aga pea neli korda väiksem (umbes 260 hPa).
Õhusamba mass
Õhurõhu põhjal võime hinnata, kui suur on Maa pinna ühele ruutmeetrile rõhku avaldavale õhusambale mõjuv raskusjõud. Võttes õhurõhuks 100 000 Pa, saame ühele ruutmeetrile mõjuva õhusamba raskusjõuks 100 000 N. Iga ruutsentimeetri kohta saame jõuks 10 N. Sama jõud mõjub ka meie keha pinna igale ruutsentimeetrile. Seda ei olegi nii vähe, kui arvestada, et inimese keha pindala on umbes 2 m2! Meie kehaehitus on selliselt välja kujunenud, et me seda rõhku ei tunneta.
Kui hinnata õhurõhku tekitava õhusamba massi, siis ühele ruutmeetrile rõhku avaldava õhusamba kogumass on umbes 10 000 kg ehk 10 tonni!
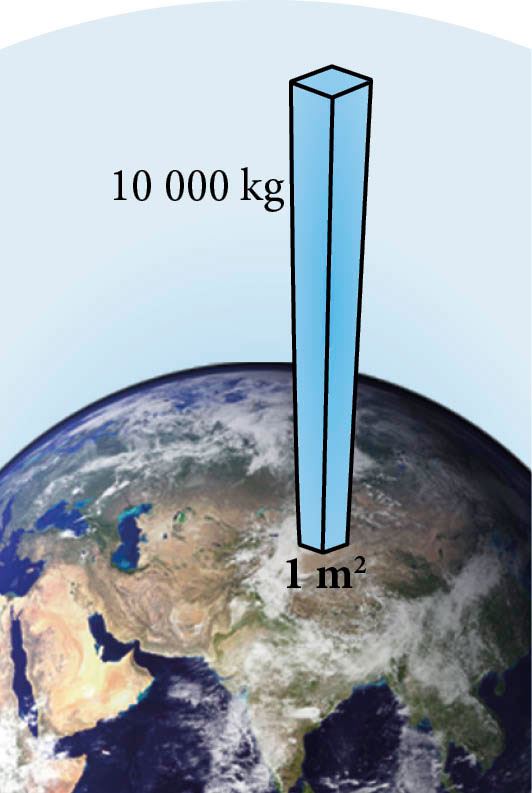
- 10 N
- 20 N
- 20 000 N
- 100 000 N
- 200 000 N
- 2 000 000 N
Rõhk vees
Eelmises õppetükis analüüsisime rõhku vedelikus, mis oli tingitud vastava vedelikusamba rõhust. Kui me aga tahame arvutada näiteks rõhku mingis veekogus, siis peame vedeliku enda tekitatud rõhule lisama veel õhurõhu, s.o ligi 100 000 Pa! Vee pinnale mõjuv õhurõhk kandub vastavalt Pascali seadusele vee sees edasi igas kohas ühtemoodi. Kümne meetri sügavusel on veesamba rõhk umbes 100 000 Pa, sellele lisandub õhurõhk 100 000 Pa ja seetõttu on kogurõhk 200 000 Pa.
Kummulipööratud klaas veega
Õpetaja tõi veeklaasi ja kiletatud paberilehe. Ta valas klaasi vett ja paberit kinni hoides pööras klaasi põhjaga ülespoole. Paberi vahelt voolas välja mõni tilk vett. Nüüd laskis õpetaja paberi lahti. Lapsed ootasid, et kogu klaasis olev vesi voolab maha. Aga oh üllatust! Paberileht jäi klaasi ette ja vesi ei voolanudki maha.
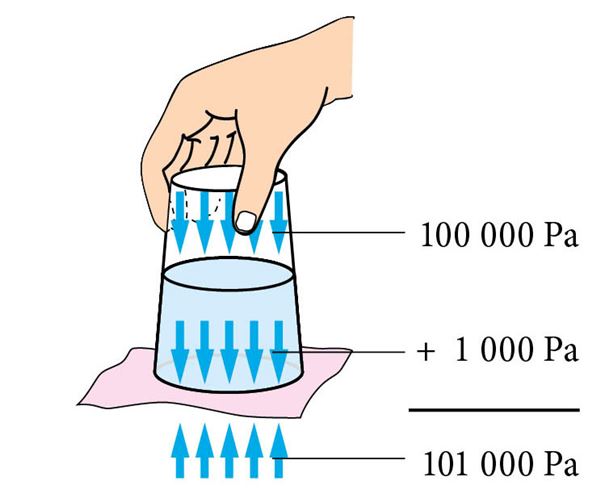
Õpetaja selgitas. Nähtus on seotud rõhkude tasakaaluga. Olgu õhurõhk 101 000 Pa. Pascali seaduse kohaselt surub õhk paberilehele alt üles. Paberilehe kohal on vesi. Kui vett on klaasis 10 cm, siis vee rõhk paberile on ülevalt poolt 1000 Pa. Vee kohal on veidi hõrendatud õhku. Õhu hõrendusest andis tunnistust see mõni tilk vett, mis välja voolas. Vee kohal oleva õhu rõhk on 100 000 Pa. Paberile altpoolt mõjub õhurõhk 101 000 Pa ning ülaltpoolt vesi ja õhk koos rõhuga 101 000 Pa. Rõhud on tasakaalus, paber püsib oma kohal ning vesi välja ei voola.
Baromeeter
Baromeeter on mõõteriist õhurõhu mõõtmiseks. Baromeetreid on kahte liiki – elavhõbebaromeeter ja aneroidbaromeeter.
Elavhõbebaromeeter
Elavhõbebaromeeter oli ajalooliselt esimene baromeeter. Elavhõbedasamba pikkust mõõdeti millimeetrites ja rõhu ühikuks sai 1 mmHg (loe: millimeeter elavhõbedasammast). Seda ühikut nimetakse õhurõhu avastaja Evangelista Torricelli auks ka torriks (1 torr = 1 mmHg).
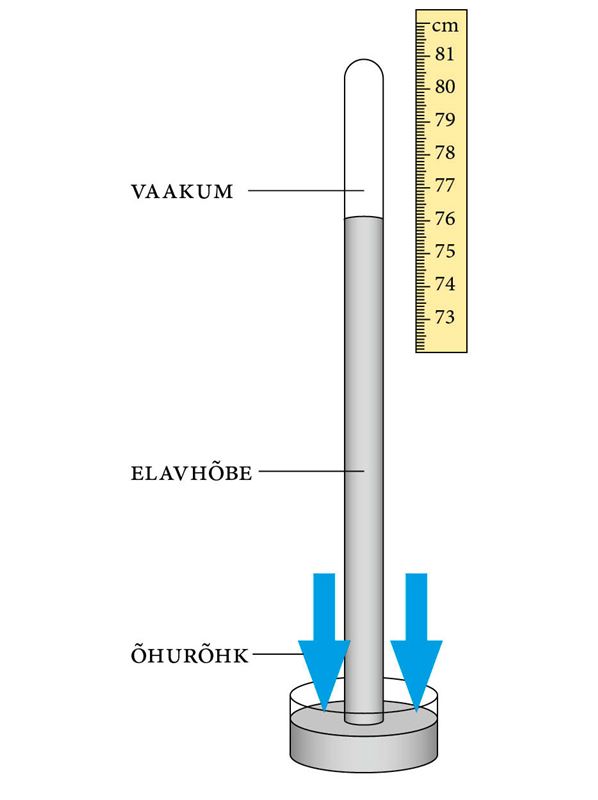
Elavhõbebaromeeter koosneb umbes 90 cm pikkusest torust, kausist ja skaalast. Kausis ja torus on elavhõbe.
Baromeetri näit võetakse elavhõbedasamba tipu juurest. Toru ülemises otsas olevas tühimikus on vaakum. Õhurõhu suurenemisel surub õhk torusse elavhõbedat juurde ja samba pikkus suureneb. Õhurõhu vähenemisel aga voolab osa elavhõbedat torust kaussi ja samba pikkus väheneb.
Aneroidbaromeeter
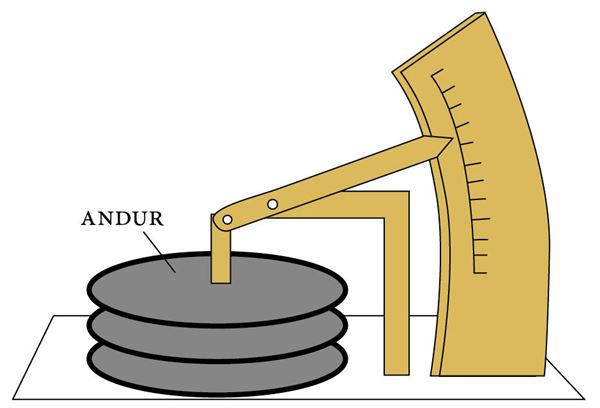
Aneroidbaromeetri põhimõtteline ehitus on toodud joonisel. Baromeetri anduriks on erilise kujuga elastsete seintega metallkarp. Karbis on hõre õhk. Õhurõhu suurenemine surub karpi kokku, selle kõrgus väheneb. Õhurohu vähenemisel lükkab karbis olev vedru karbi külgi lahku, selle kõrgus suureneb. Karbi mõõtmete muutus kajastub osuti nihkes. Osuti näit annab õhurõhu väärtuse.
Pean meeles
Õhk avaldab rõhku.
Normaalrõhk on 1013 hPa ehk 760 mmHg.
Ilmateates antakse õhurõhk merepinna kõrgusel.
Küsimusi ja ülesandeid
- Vasta õppetüki alguses olevale küsimustele.
- Kui suur on inimese keha pinnale mõjuv õhurõhust tingitud jõud, kui tema keha kogupindala on 1,5 m2?
- Millised on õhurõhu ühikud?
- Milline on elavhõbebaromeetri tööpõhimõte?
- Milline on aneroidbaromeetri tööpõhimõte?
- Miks iminapp kinnitub pinnale?
- Kuidas kaheksajalg kividele kinnitub?