Võrdust, mis võimaldab igal ajahetkel t arvutada mööda mingit joont liikuva keha kaugust s lähtepunktist O, nimetatakse vaadeldava keha liikumisseaduseks.
Olgu keha liikumisseadus üldjuhul antud võrdusega s = f (t). Vaatleme keha liikumist hetkest t hetkeni t + Δt, s.t ajavahemikus Δt. Et läbitud tee pikkused nendel hetkedel on f (t) ja f (t + Δt), siis ajavahemikus Δt läbitud tee pikkus on
ja keskmine kiirus
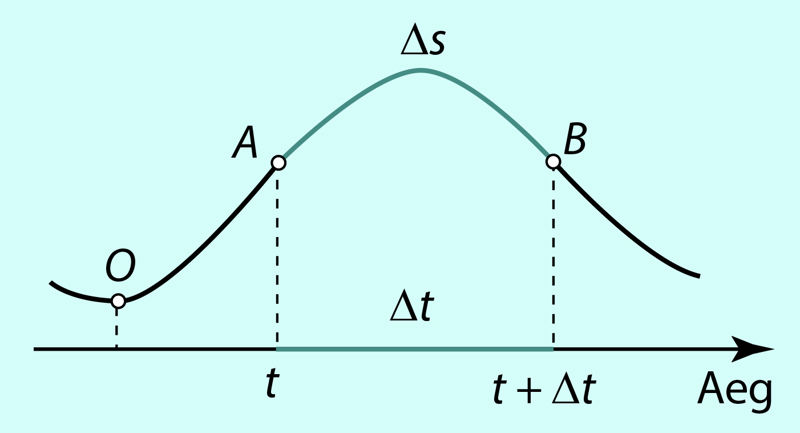
Joonisel 4.10 on kujutatud läbitud tee OAB ja selle all ajatelg (aja t kasvades suurus s kasvab). Ajavahemikule Δt vastav läbitud tee on AB. Keskmine kiirus vk on arvutatud ajavahemiku Δt jooksul või, teisiti öeldes, teelõigul Δs = AB. Soovime nüüd teada, kui suur oli liikuva objekti kiirus punktis A, s.o hetkel t. Seda kiirust nimetatakse hetkkiiruseks ja tähistatakse tähega v. Keskmine kiirus vk iseloomustab hetkkiirust v seda paremini, mida väiksem on Δs või, teisiti öeldes, mida väiksem on ajavahemik Δt.
Järelikult,
kui
Vaadeldes liikumisseadust s = f (t) funktsioonina, võime üldistavalt öelda, et hetkkiirus on suurus v, millele läheneb funktsiooni muudu Δs ja argumendi muudu Δt suhe, kui argumendi muut läheneb nullile.
Kasutades funktsiooni piirväärtuse mõistet, on eelöeldu põhjal
ehk
Sõnastatult: hetkkiirus on funktsiooni s = f (t) muudu Δs ja argumendi muudu Δt suhte piirväärtus, kui argumendi muut läheneb nullile.
Näide.
Veendume, et vaba langemise seadusest
Kuna
Nüüd:
kui Δt → 0, siis
või
Seos v = gt on tõesti füüsikakursusest tuntud vaba langemise hetkkiiruse valem.
