Ülesanne 288. Jada üldliige
1; 3; 5; 7; 9; ; ; …
12; 8; 4; 0; –4; ; ; …
–2; –5; –8; –11; –14; ; ; …
- Leidke neis seaduspärasused ja jätkake antud jadasid kahe liikme võrra.
- Mida ühist märkate antud jadades, võrreldes järjestikuseid liikmeid?
- Esitage iga jada üldliige valemiga. Võrrelge neid.
1; 3; 5; 7; 9; … | |
12; 8; 4; 0; –4; … | |
–2; –5; –8; –11; –14; … | |
Jada, milles teisest liikmest alates on iga liikme ja sellele eelneva liikme vahe konstantne, nimetatakse aritmeetiliseks jadaks.
Konstantset arvu an – an–1 nimetatakse aritmeetilise jada vaheks ja tähistatakse tähega d. Seega aritmeetilises jadas an = an–1 + d iga n > 1 korral.
Näide.
Jada 7; 12; 17; 22; …; 5n + 2; … on aritmeetiline jada, sest 12 – 7 = 17 – 12 = 22 – 17 = … = 5. Selle jada vahe d = 5.
Jada 2; 6; 18; 54; … ei ole aritmeetiline jada, sest 6 – 2 ≠ 18 – 6 ≠ 54 – 18.
Kui a1 = 1 ja d = 1, saame aritmeetilise jada 1; 2; 3; 4; …; n; … .
Kui a1 = 3 ja d = 0, saame aritmeetilise jada 3; 3; 3; … . See on konstantne jada.
Kui jada vahe d > 0, siis on aritmeetiline jada kasvav; kui d < 0, siis on tegemist kahaneva jadaga.
Aritmeetilise jada üldliige
Kui on teada aritmeetilise jada esimene liige a1 ja jada vahe d, siis on võimalik leida jada mis tahes liiget:
a2 = a1 + d;
a3 = a2 + d = a1 + d + d = a1 + 2d;
a4 = a3 + d = a1 + 2d + d = a1 + 3d;
ehk üldiselt an = a1 + (n – 1)d.
Aritmeetilise jada (an) üldliige avaldub kujul an = a1 + (n – 1)d.
Näide 1.
Olgu aritmeetilises jadas teada a8 = 172 ja a1 = –3. Leiame aritmeetilise jada vahe d.
Et a8 = a1 + 7d, siis 7d = a8 – a1 = 172 + 3 = 175 ja d = 175 : 7 = 25.
Näide 2.
Leiame, mitmes liige on arv 100 aritmeetilises jadas, milles a1 = 2 ja d = 2.
Valemist an = a1 + (n – 1)d saame, et
Ülesanded A
Ülesanne 289. Aritmeetiline jada
Antud arvud | Kas on aritmeetiline jada? | Jada vahe |
5; –1; –7; –13; … |
| d = |
| d = | |
12; 4; |
| d = |
2; 8; 14; 20; … |
| d = |
Ülesanne 290. Aritmeetiline jada
Ülesanne 291. Aritmeetiline jada
Ülesanne 292. Aritmeetiline jada
Jada nr | a1 | d | n | an |
1. | 15 | –3 | 10 | |
2. | –21 | 4 | 25 | |
3. | –9 | 11 | 21 | |
4. | –8 | 15 | –29 | |
5. | 23 | –5 | –22 | |
6. | –16 | 3 | 20 |
Ülesanne 293. Funktsioonidega määratud jadad
1) y = –2x + 1 | 2) y = 1 – x2 | 3) | ||
4) y = 3(1 + x) | 5) | 6) y = 4x + 1 |
- Esitage antud funktsioonidega määratud jadade 4 esimest liiget ja n-es liige. Selleks andke argumendile x järjestikuseid naturaalarvulisi väärtusi 1; 2; 3; 4 ja n. Kandke liikmetele a1, a2, a3 ja a4 vastavad punktid koordinaattasandile.
- Missugused saadud jadadest on aritmeetilised jadad? Kuidas nimetatakse neid määravaid funktsioone?
Vastus. Saadud jadadest on aritmeetilised jadad
- 1)
- 2)
- 3)
- 4)
- 5)
- 6)
Neid määravad .
- Kuidas avalduvad saadud aritmeetiliste jadade vahed esialgse funktsiooni valemis olevate kordajate kaudu?
- Kas punktides 2 ja 3 leitu kehtib iga sellist liiki funktsiooni korral? Defineerige aritmeetiline jada vastava funktsiooni väärtuste jada kaudu.
Ülesanne 294. Kaldpinnal veerev keha
Vastus. Keha läbis 10. sekundiga m.
Ülesanne 295. Jalgrattur
Vastus. Jalgrattur sõidab h.
Ülesanne 296. Aritmeetiline jada
Ülesanne 297. Aritmeetiline jada
Vastus. Need arvud on , , , , , .
Ülesanne 298. Aritmeetiline jada
Vastus. Need arvud on
Ülesanne 299. Tõestamine
- Uurige, kuidas on jada iga liige seotud oma kahe naaberliikmega.
- Tõestage leitud seos.
- Millest võiks olla aritmeetiline jada saanud oma nimetuse?
Ülesanne 300. Aritmeetiline jada
Vastus. a6 + a8 =
Ülesanded B
Ülesanne 301. Tõestamine
Kui suur on kumera 21-nurga sisenurkade summa?
Vastus. Kumera 21-nurga sisenurkade summa on
Ülesanne 302. Tõestamine
Ülesanne 303. Aritmeetiline jada
Vastus. Antud tingimus on täidetud esimese liikme korral.
Ülesanne 304. Aritmeetiline jada
Ülesanne 305. Aritmeetiline jada
Vihje
Ülesanne 306. Aritmeetiline jada
Aritmeetilise jada n esimese liikme summa
Kui saksa matemaatik Carl Friedrich Gauss (1777–1855) oli 9-aastane, andis õpetaja klassile ülesande: leida kõigi naturaalarvude summa 1-st kuni 100-ni. Ta lootis, et õpilastel jätkub arvutamist terveks tunniks või kauemakski. Vaevalt oli õpetaja ülesande andnud, kui Gauss oma tahvli ülesande vastusega õpetajale ulatas. Kuidas jõudis ta nii kiiresti vastuseni?
Noore Gaussi poolt avastatud seaduspärasus on paremini märgatav, kui arvud 1–100 esitada kahe osana: alumistes tulpades arvud 1–50 ja nende peal olevates tulpades arvud 51–100 (joonis 2.4). Näeme, et 1 + 100 = 2 + 99 = 3 + 98 = … = 101. Et selliseid summasid on kokku 50, on ülesande vastuseks 50 · 101 = 5050.
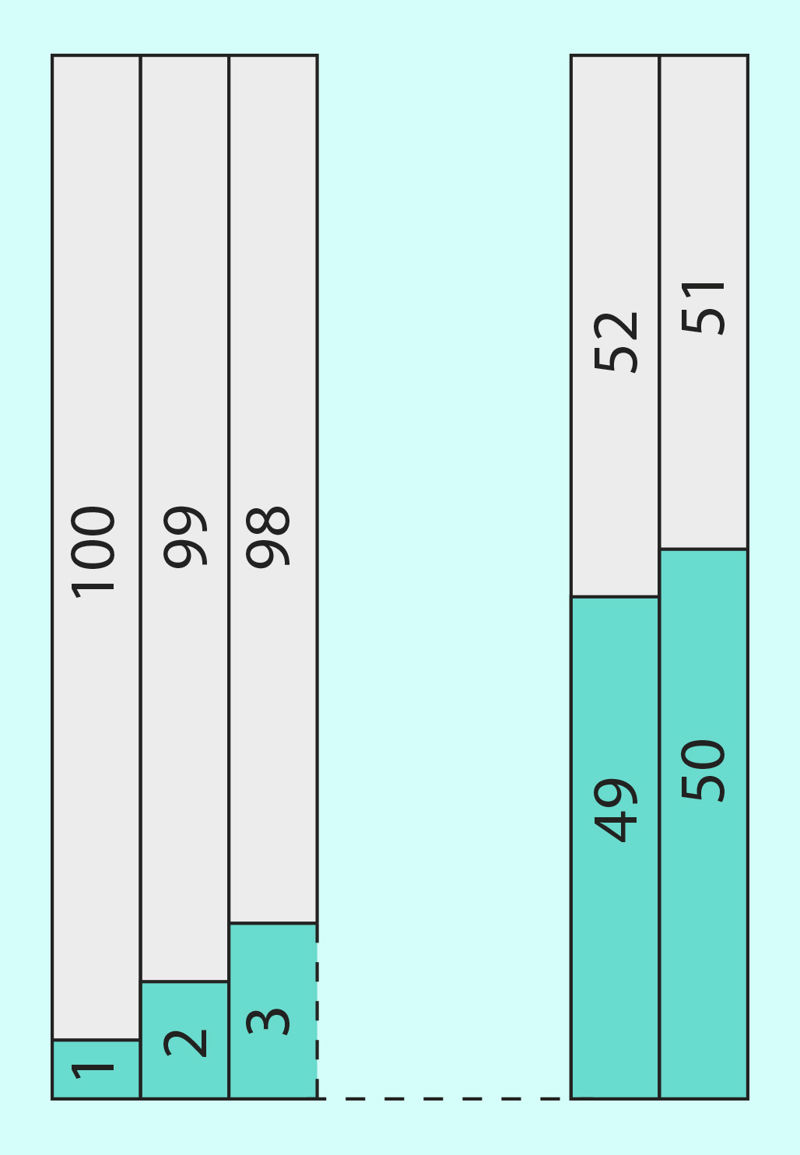 Joon. 2.4 | ||||||
TEOREEM. Kui võtta aritmeetilises jadas n järjestikust liiget, siis on selles jadas algusest ja lõpust võrdsel kaugusel seisvate liikmete summa jääv ning võrdub esimese ja viimase liikme summaga.
Tõestus.
Olgu antud aritmeetilise jada (an) n järjestikust liiget
a1, a2, a3, …, an–2, an–1, an.
Sel juhul on algusest ja lõpust esimesel kohal olevate liikmete summa a1 + an. Algusest ja lõpust teisel kohal olevate liikmete summa on
a2 + an–1 = a1 + d + an – d = a1 + an.
Vaatleme algusest ja lõpust k-ndate liikmete summat. Teame, et lõpust 2. liikme indeks on n – 1, lõpust 3. liikme indeks n – 2 jne, lõpust k-nda liikme indeks on n – (k – 1) = n – k + 1. Jada üldliikme valemi järgi
ak = a1 + (k – 1)d, an–k+1 = a1 + [(n – k + 1) – 1]d = a1 + (n – k)d
ja seega
ak + an–k+1 = a1 + (k – 1)d + a1 + (n – k)d = a1 + kd – d + a1 + nd – kd = a1 + a1 + (n – 1)d = a1 + an. ♦
Saadud omadust kasutades tuletame valemi aritmeetilise jada n esimese liikme summa Sn arvutamiseks. Esitame summa Sn kaks korda: üks kord on summas jada liikmed nende loomulikus järjestuses, teine kord vastupidises järjestuses.
(1) Sn = a1 + a2 + a3 + … + an–2 + an–1 + an
(2) Sn = an + an–1 + an–2 + … + a3 + a2 + a1
Nagu äsja tõestasime, on võrduste paremal pool kohakuti paiknevate liikmete summad võrdsed. Et selliseid summasid on n tükki, saame võrduste (1) ja (2) vastavate poolte liitmisel 2Sn = (a1 + an)n, millest saame valemi aritmeetilise jada n esimese liikme summa arvutamiseks:
Teades, et an = a1 + (n – 1)d, võime saadud valemile anda ka teise kuju:
Viimane valem võimaldab arvutada n esimese liikme summat vaid jada esimese liikme ja jada vahe järgi. Kui d = 0, siis Sn = a1 · n.
Näide 1.
Leiame summa 1 + 2 + 3 + … + n. Siin on liidetavateks aritmeetilise jada n järjestikust liiget ja a1 = 1, d = 1, an = n.
Näide 2.
Leiame kõigi 100-st väiksemate paaritute naturaalarvude summa. Esimene paaritu naturaalarv a1 = 1 ja viimane an = 99. Tarvis on teada veel liikmete arvu n, mille leiame jada üldliikme valemist an = a1 + (n – 1)d:
Siis
Ülesanded A
Ülesanne 307. Aritmeetilise jada 10 esimese liikme summa
Ülesanne 308. Aritmeetilise jada n esimese liikme summa
Ülesanne 309. Kaldpinnal veerev keha
Vastus. Keha läbis 10 sekundiga
Ülesanne 310. Tartu Raekoja kell
Vastus. Tartu Raekoja kell lööb ööpäevas korda.
Ülesanne 311. 7-ga jaguvad arvud
Vastus. Arvude 100 ja 1000 vahel on 7-ga jaguvat arvu. Nende arvude summa on .
Ülesanne 312. Tõestamine
Ülesanne 313. Vabalt langev keha
Ülesanne 314. Töölise teenistus
Vastus. Firmas A teeniks ta 10 aastaga € ja firmas B sama ajaga €.
Ülesanne 315. Aktsiatulu
Vastus. Tulu iga-aastane juurdekasv oli €. Omanik sai aktsiatelt 11 aastaga € tulu.
Ülesanne 316. Veetrassi torud
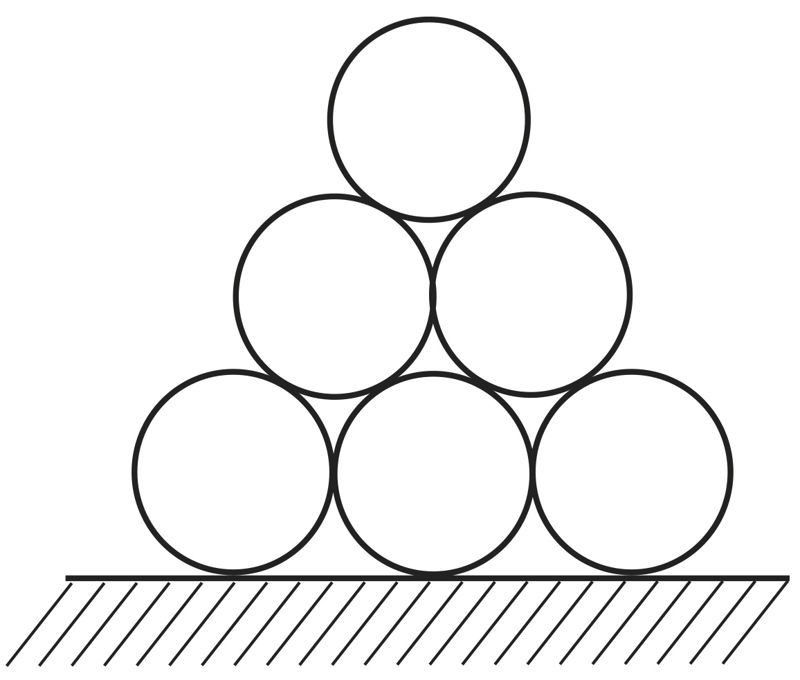
Vastus. 120 toru paigutamisel tekib -realine virn ja kõige alumisse ritta tuleb panna toru. Virna kõrgus saab olema m.
Ülesanne 317. Aritmeetilise jada liikmete summa
Vastus. Selles jadas tuleb võtta liiget.
Ülesanne 318. Jalgratturite matkagrupp
Vastus. Matkagrupp jõudis sihtkohta kell .
Ülesanded B
Ülesanne 319. Kolmekohaliste naturaalarvude summa
Vastus. Kõigi selliste kolmekohaliste naturaalarvude summa on .
Ülesanne 320. Aritmeetilise jada 40 esimese liikme summa
Vastus.
Ülesanne 321. Avaldamine
Vastus. an =
Ülesanne 322. Aritmeetilise jada liikmete arv
Vastus. n =
Ülesanne 323. Poegade vanused
Vastus. Poegade vanused on (alates noorimast) a, a, a, a ja a.
