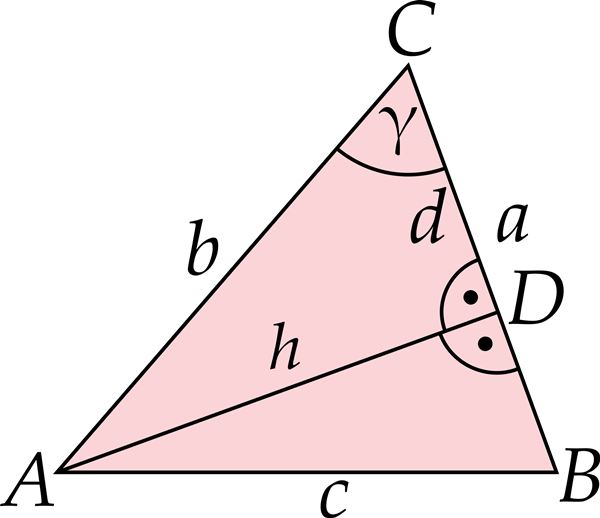
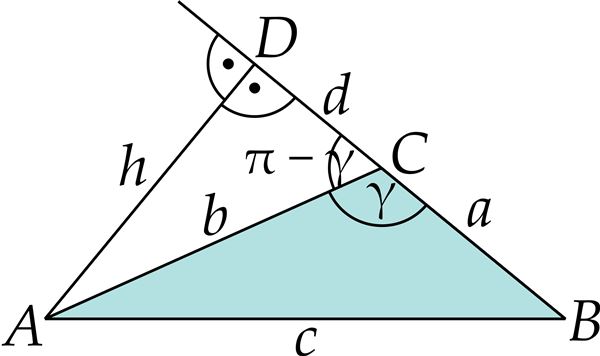
- Koosinusteoreemi tõestamine
- Koosinusteoreemi rakendamine kolmnurga puuduvate elementide arvutamiseks
Koosinusteoreem
Koosinusteoreem on Pythagorase teoreemi üldistus juhul, kui kolmnurga külgedevaheline nurk pole täisnurk, vaid mingi terav- või nürinurk.
Koosinusteoreem
Kolmnurga ühe külje ruut võrdub teiste külgede ruutude summaga, millest on lahutatud teiste külgede ja nendevahelise nurga koosinuse kahekordne korrutis.
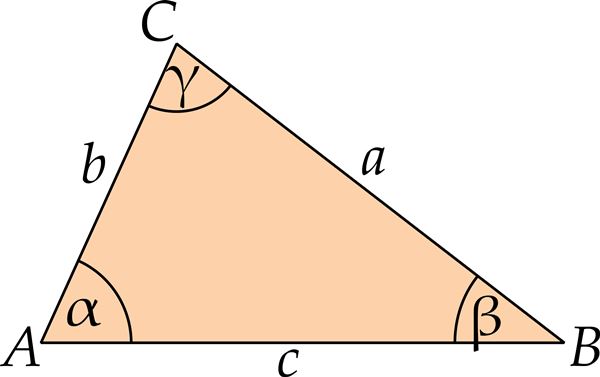
- a2 = b2 + c2 – 2bc⋅ cos α
- b2 = a2 + c2 – 2ac⋅ cos β
- c2 = a2 + b2 – 2ab⋅ cos γ.
Märka
Kui koosinusteoreemi võrduses eeldada, et külje c vastas ning seega külgede a ja b vahel on täisnurk siis ja saamegi Pythagorase teoreemi väite c2 = a2 + b2 ehk hüpotenuusi ruut võrdub kaatetite ruutude summaga.
Selles kolmnurgas kehtivad laused
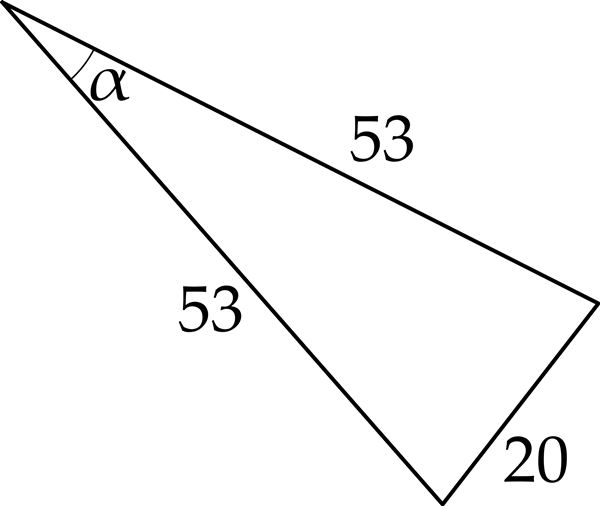
α ≈ °
- 20² = 53² + 53² – 2 · 53² · cos α
- 20 = 53 + 53 – 2 · 53² · cos α
- 20² = 2 · 53² – 2 · 53²· cos α
- 400 – 5618 = –5618 · cos α
- 5618 · cos α = 5218
- 5618 · cos α = –5218
- cos α ≈ 0,9288
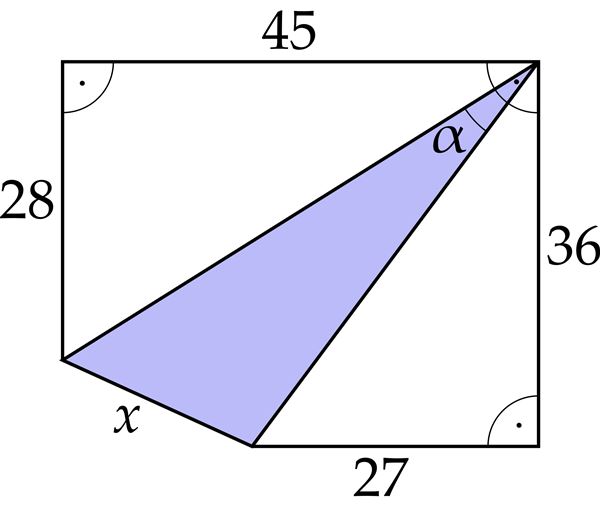
α ≈ °
- nurga α lähisküljed
- lühem
- pikem
- x2 ≈ (koosinusteoreemist)
x2 = (Pythagorase teoreemist) - x ≈
Harjutan ja lahendan
1. kolmnurk | 2. kolmnurk | 3. kolmnurk | |
a | 29 | 20 | 8 |
b | 28,8 | 6,5 | |
c | 20 | 38 | |
α | ° | ° | 40° |
β | ° | ° | ° |
γ | ° | 72° | ° |
Vastus. Rööpküliku lühem diagonaal on cm ja pikem diagonaal cm.
Jäta meelde
1.
, kus R on
2.
- = b² + c² – 2 bc · cos
- = a² + c² – 2 ac · cos
- = a² + b² – 2 ab · cos
3.
- = 0,5 ab · sin
- = 0,5 bc · sin
- = 0,5 ac · sin