Для доказательства теорем в математике часто пользуются так называемым методом доказательства от противного, в основе которого лежит один из законов логики: для каждого утверждения истинно либо само утверждение, либо его отрицание, третьего быть не может. В этом случае предполагают, что заключение теоремы не является истинным, а истинным является его отрицание. В ходе рассуждения показывают, что отрицание заключения теоремы приводит к противоречию с условием теоремы или с каким-нибудь истинным утверждением. Отсюда следует, что отрицание доказываемого заключения теоремы не может быть истинным, и, значит, истинным является заключение теоремы.
При доказательстве от противного надо уметь строить отрицания утверждений. Научись и ты этому.
- Солнце светит.
- Вода – мокрая.
- Высота класса равна 5 м.
- Прямые a и b пересекаются.
- Число x делится на 3.
- Треугольник является тупоугольным.
- Прямые a и b не параллельны.
- Число a не является положительным.
- x < 0.
- m ≥ 0.
- Число 9 делится на 3.
Отрицание:
Истинным является .
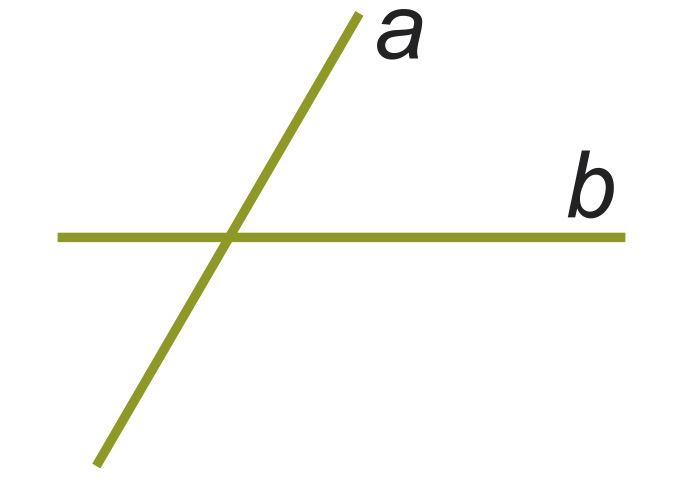
- Прямые a и b на рисунке пересекаются.
Отрицание:
Истинным является .
- Прямые a и b на рисунке перпендикулярны.
Отрицание:
Истинным является . - Прямые a и b на рисунке параллельны.
Отрицание:
Истинно . - a3 = a · a · a · a.
Отрицание:
Истинно . - 7 + 5 = 75.
Отрицание:
Истинно .
Рассмотрим некоторые примеры на доказательство от противного. Но сначала вспомним определение параллельных прямых: две прямые называются параллельными, если они расположены на одной плоскости и не пересекаются.
 |
||||||
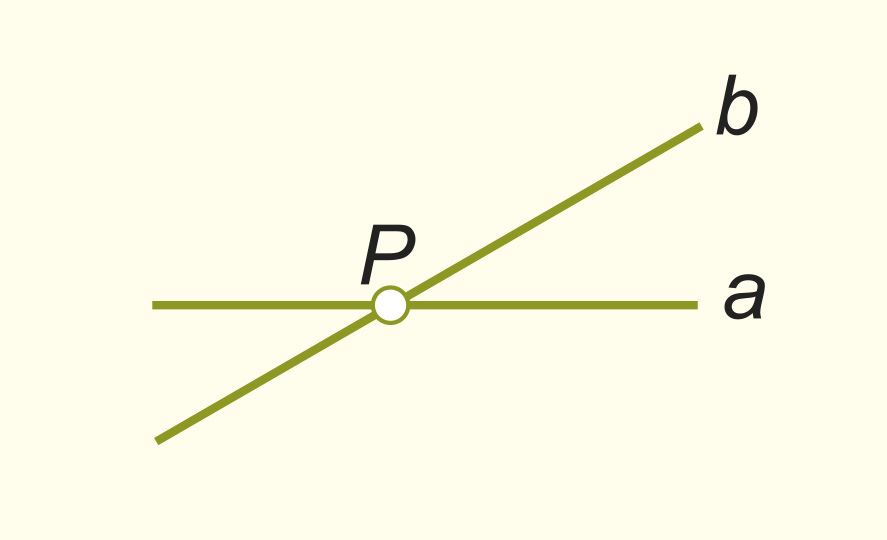
Прямые a и b не параллельны, а пересекаются в точке P.
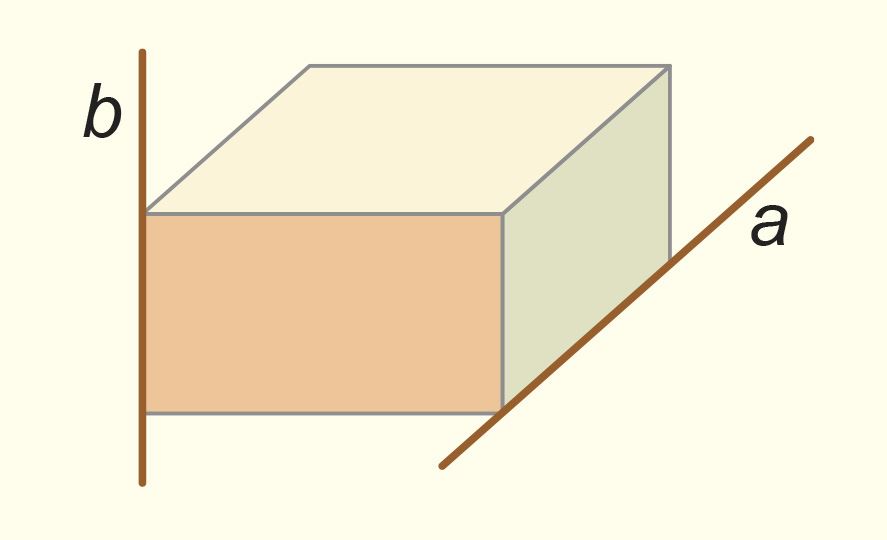
Прямые a и b не пересекаются, но не лежат в одной плоскости. Прямые a и b не являются параллельными.
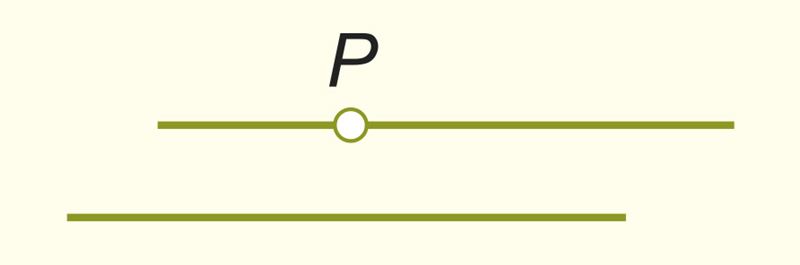
Основное свойство параллельных прямых выражается аксиомой параллельных прямых: через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной прямой.
 |
||||||

1. Если две прямые a и b параллельны третьей прямой с, то они параллельны друг другу.
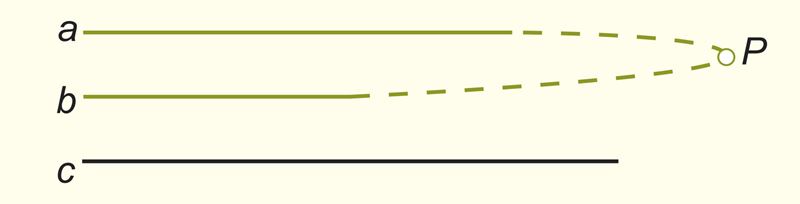
Условие. a || c и b || c (см. рисунок).
Заключение. a || b.

Доказательство (от противного). Предположим, что справедливо отрицание доказываемого утверждения, т. е. прямые a и b не параллельны. Это утверждение предполагает, что прямые пересекаются в некоторой точке P (см. рисунок), так как на плоскости третьей возможности быть не может.
Но в этом случае через точку P проходят две различные прямые, которые обе параллельны прямой c. Однако это противоречит аксиоме параллельных прямых. Следовательно, прямые a и b не пересекаются, т. е. они параллельны. ■

2. Если прямая с пересекает одну из двух параллельных прямых a и b, то она пересекает и другую прямую.
Условие. a || b и c пересекается с прямой b.
Заключение. Прямая c пересекает прямую b.
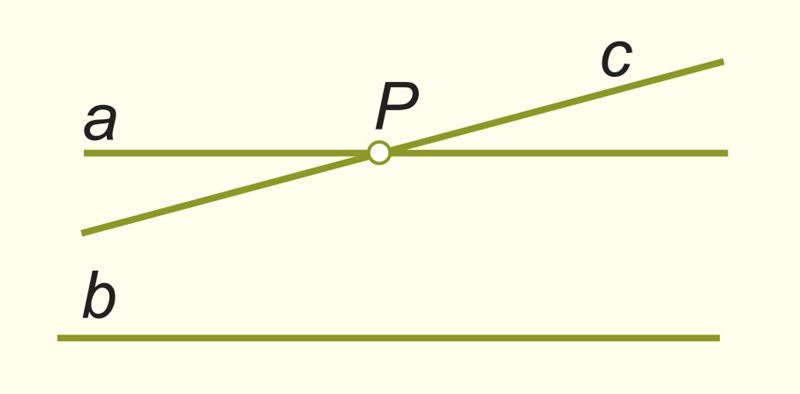
Доказательство (от противного). Сделаем предположение, противоположное тому, что утверждается в теореме, т. е. допустим, что прямые c и b не пересекаются. Отсюда следует, что c || b. Но в этом случае через точку P проходят две прямые a и c, каждая из которых параллельна прямой b. Это противоречит аксиоме параллельных прямых. Следовательно, прямые c и b должны пересекаться. ■

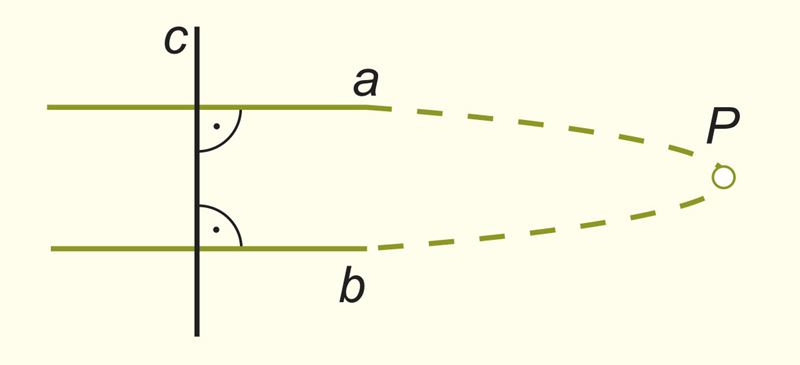
3. Если две прямые a и b перпендикулярны третьей прямой c, то прямые a и b параллельны.
Условие. a ⊥ c и b ⟘ c.
Заключение. a || b
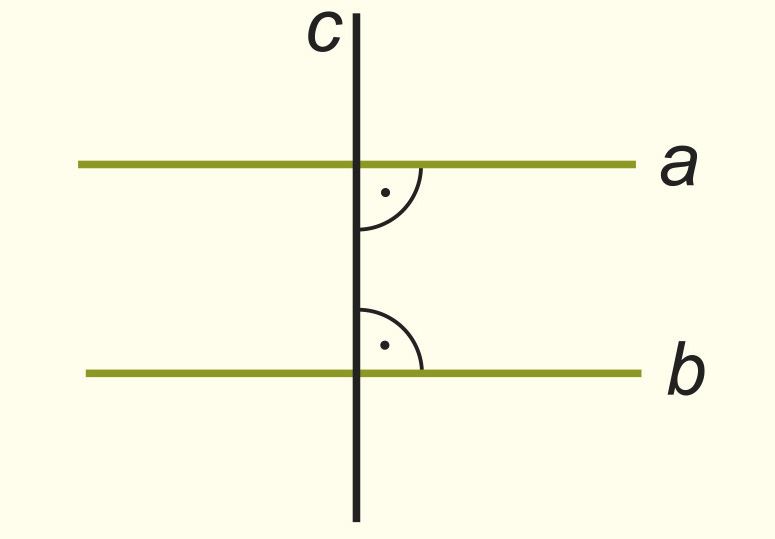
Докажи эту теорему самостоятельно методом доказательства от противного, пользуясь рисунком. Какому утверждению противоречит предположение о том, что прямые a и b не параллельны?
Упражнения A
 |
||||||||
- Если радиаторы центрального отопления горячие, то в комнате тепло.
- В моей комнате не тепло.
Вывод:
Обоснование:
- Все жители Вильянди живут в Эстонии.
- Анна не живет в Эстонии.
Вывод:
Обоснование:
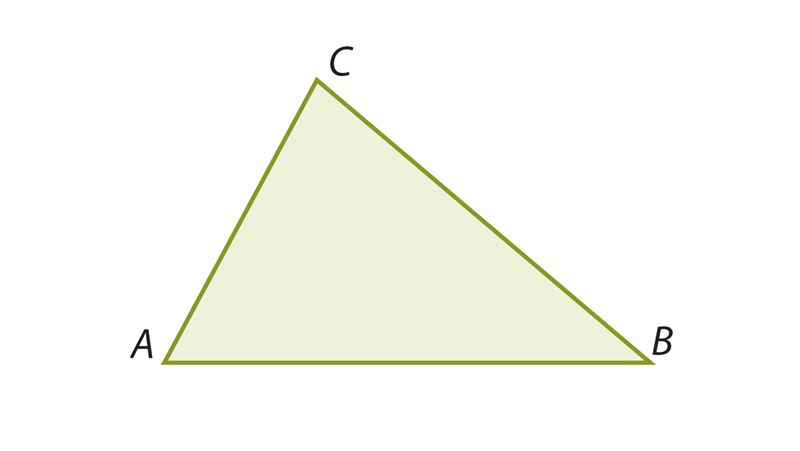
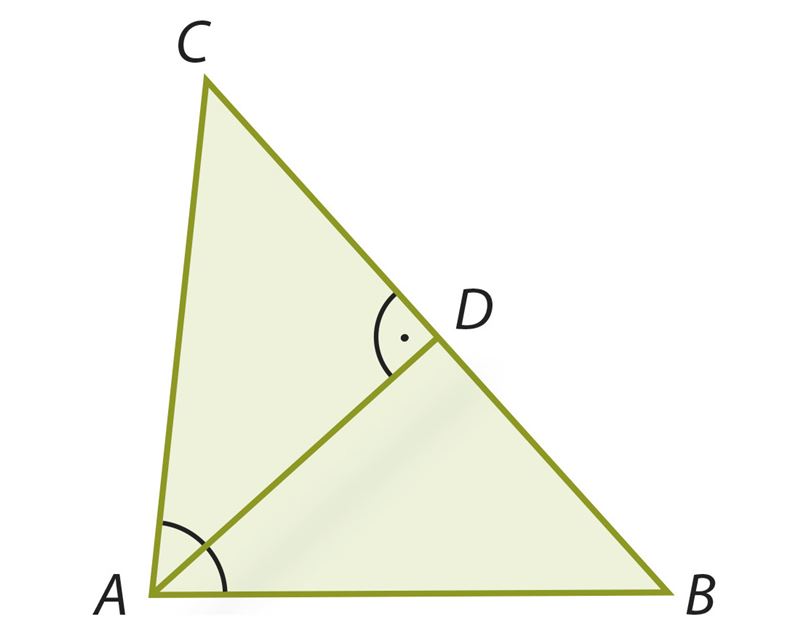
∠A ≠ ∠B ⇒ BC ≠ AC
Упражнения Б
 |
||||||||
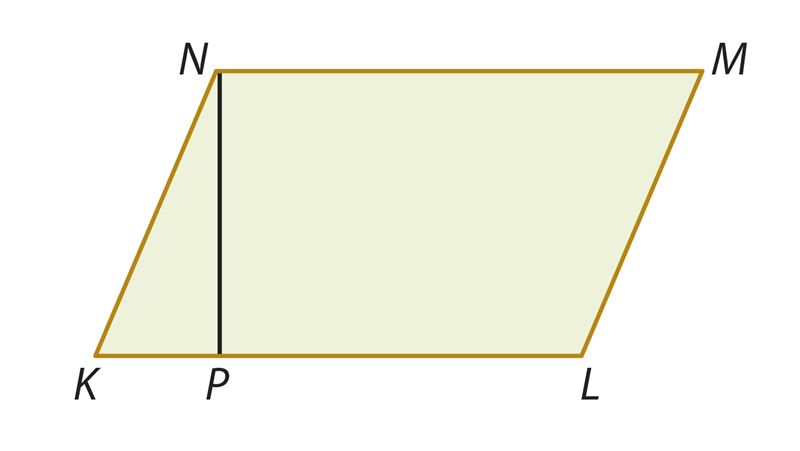
- Сформулируй утверждение, которое нужно доказать.
- Сформулируй отрицание доказываемого, т. е. сделанное предположение.
- Какое следствие вытекает из сделанного предположения?
- Сформулируй утверждение, которому противоречит предыдущее следствие.