Kahe statistilise kogumi sagedustabelid on järgmised:

Mõlema kogumi korral on N = 28,
Mingil määral iseloomustab hajuvust tunnuse muutumispiirkond (või selle pikkus – variatsioonrea ulatus), s.t piirkond minimaalsest väärtusest maksimaalse väärtuseni. Praeguse näite korral on need mõlema kogumi puhul samad, xmin = 7, xmax = 13. Seega ka see näitaja ei ütle alati, kummal juhul on hajuvus suurem.
Seame eesmärgiks leida karakteristiku, mis iseloomustab tunnuse hajuvust aritmeetilise keskmise suhtes.
Tunnuse üksiku väärtuse xi kõrvalekallet (erinevust) keskmisest
Kogu variatsioonrea (andmestiku) kui terviku hajuvust
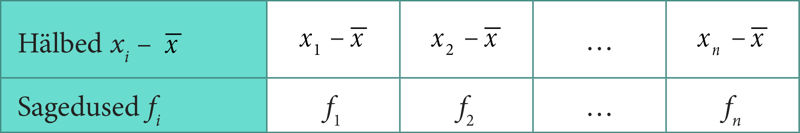
Et saadud tabeli põhjal on vahetult raske midagi otsustada tunnuse hajuvuse üle, oleks tarvis vastavat koondnäitajat, karakteristikut. Võib tunduda, et selleks sobib keskmine hälve (hälvete aritmeetiline keskmine). Kuid see on alati null, sest juba
aritmeetilise keskmise suhtes arvutatud hälvete summa on null, s.t .
Tõepoolest:
Et vältida hälvete vastastikust koondumist nulliks, kasutatakse hajuvust iseloomustava suurusena hälvete ruutude (saame positiivsed arvud) aritmeetilist keskmist, mida nimetatakse dispersiooniks ja tähistatakse sümboliga σ2 (ka s2), arvutipõhistes arvutussüsteemides VARP.
Seega on
Mida suurem on σ2, seda suurem on tunnuse väärtuste hajuvus.
Saadud karakteristikul on hajuvuse iseloomustajana üks puudus – tema ühikuks on tunnuse ruutühik. Et sellest ebakõlast vabaneda, kasutatakse hajuvuse karakteristikuna standardhälvet σ (ka sümbol s):
Arvutipõhistes arvutussüsteemides esineb sümbol STDEVP.
Enamiku tunnuste korral erineb üle poole andmetest aritmeetilisest keskmisest vähem kui standardhälbe σ võrra. Teisiti öeldes paikneb tavaliselt enamik tunnuse väärtustest piirkonnas
Näide 1.
Leiame käesoleva peatüki alguses esitatud statistiliste andmete korral standardhälbed. Arvutused vormistame arvutuste lihtsustamise ja arusaadavuse huvides tabelina. Mõlemal juhul oli
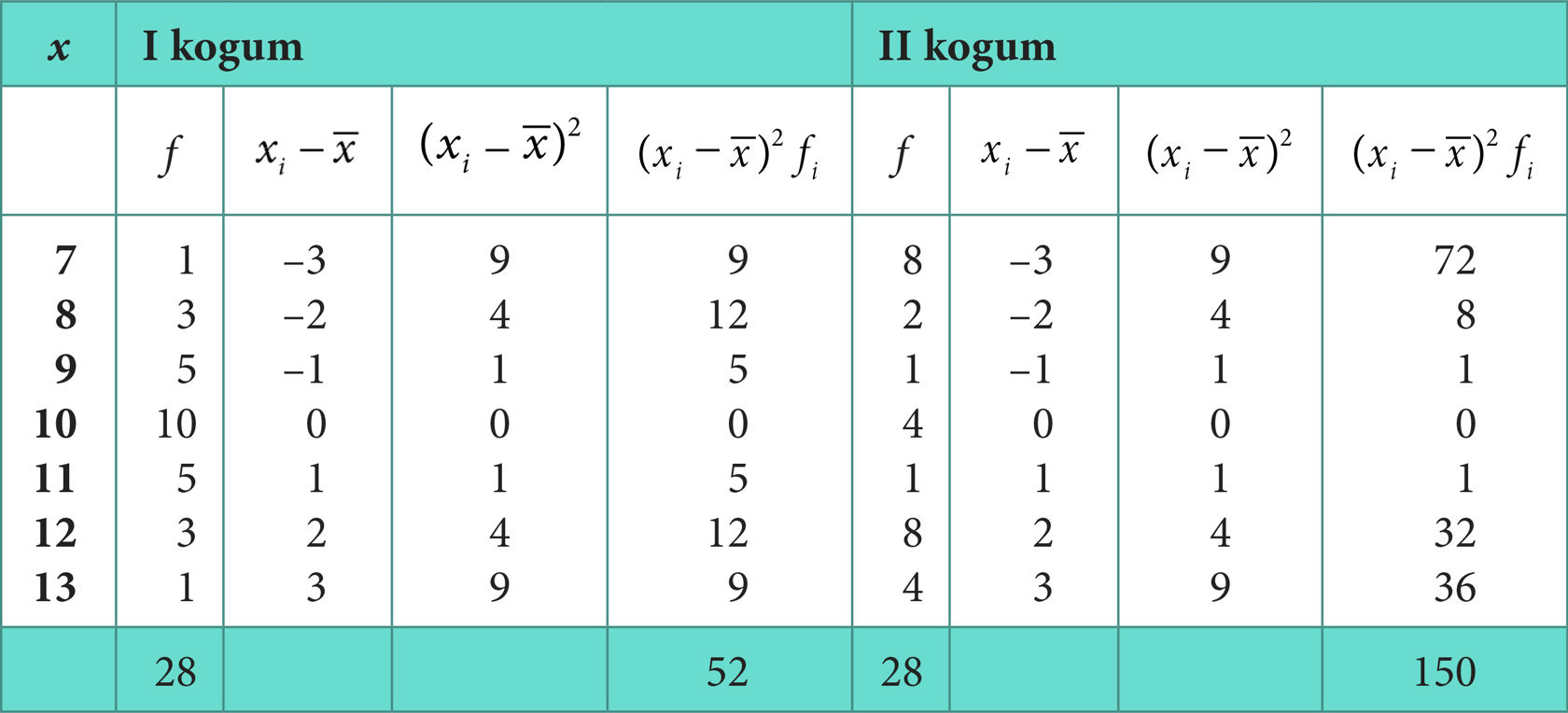
I kogumi korral on
Dispersiooni σ2 arvutamiseks saab defineerivast võrdusest tuletada praktilisema valemi
kus
Kasutades dispersiooni või standardhälbe valemit, võib leida hajuvuse mitte ainult aritmeetilise keskmise, vaid ka mõne teise arvu suhtes.
Näide 2.
Näites 1 vaadeldud II kogumi korral on tunnuse väärtuste hajuvus mo = 12 suhtes
Aritmeetilise keskmise suhtes oli see 2,31.
Osutub, et tunnuse väärtuste hajuvus aritmeetilise keskmise suhtes on alati väiksem kui mis tahes teise arvu suhtes, ehk teisiti,
tunnuse väärtused paiknevad kõige tihedamini aritmeetilise keskmise ümber.
Kahe kogumi võrdlemine hajuvuse seisukohalt taandub standardhälvete võrdlemisele. Nii tehakse näiteks ülesande 174 lahendamisel ja see on õigustatud, sest vastavad keskmised ei ole eriti erinevad. Kui see aga on nii, näiteks tahetakse võrrelda algkooli poiste ja täiskasvanud meeste pikkuse hajuvust vastavate keskmiste suhtes, ei ole selliselt õige toimida. Põhjuseks on liiga erinev pikkuste tase, mis avaldub ka aritmeetiliste keskmiste erinevuses. Niisugusel juhul on sobivam leida suhteline hajuvus, võrreldes keskmisega. See on
mida nimetatakse variatsioonikordajaks, ja nagu ikka suhtarvu, võib selle esitada ka protsentides. Variatsioonikordajal on mõte vaid siis, kui tunnuse väärtused on positiivsed. Analoogiline situatsioon on erinevates ühikutes (näiteks sentimeetrites ja kilogrammides) mõõdetud tunnuste hajuvuse võrdlemisel. Nii näiteks tuleb kasutada variatsioonikordajat, kui uuritakse, kas 11. klassi noormeeste kehakaalu või pikkuse hajuvus on suurem.
Ülesanded A
Ülesanne 174. Kontrolltöö tulemused
 | ||||||
Leidke hinnete aritmeetiline keskmine ja standardhälve ning hinnake, kummas klassis tehti kontrolltöö paremini. Kui palju hindeid (ka protsentides) paikneb kummalgi juhul piirkonnas
Vastus. A klassis oli hinnete aritmeetiline keskmine ja standardhälve ning B klassis oli hinnete aritmeetiline keskmine ja standardhälve . Järelikult kontrolltöö tehti paremini klassis. Piirkonnas
Ülesanne 175. Algaja laskuri tulemused

Leidke laskuri tulemuste hajuvus. Kui palju tulemustest paikneb piirkonnas
Vastus. σ = . Piirkonnas
Ülesanne 176. Neidude ja noormeeste pikkuste hajuvus
Ülesanne 177. Kontrolltöö hinnete hajuvus
Leidke oma klassi viimase matemaatika kontrolltöö hinnete hajuvus, leidke ka piirkond
