Statistiline andmestik

Üsna sageli tahetakse uurida inimeste, olendite, esemete või nähtuste kogumit (hulka) kui tervikut mingi omaduse või tunnuse seisu­kohalt. Nii näiteks võidakse tunda huvi, milline on Eestis elavate 17-aastaste noor­meeste keskmine pikkus, kummas paralleel­klassis läks matemaatika eksami­töö paremini, kuidas jaotuvad ette­võtted Eestis tööliste arvu järgi, milline on lilla sireli õite jaotus õie­lehtede arvu järgi. Kuidas koguda vastavaid andmeid, neid esitada, uurida ja järeldusi teha – sellega tegeleb matemaatika osa, mille nimetuseks on matemaatiline statistika. Matemaatiline statistika tugineb see­juures suuresti tõenäosus­teooriale.

Uuritavat kogumit, mille kui terviku kohta tahetakse järeldusi teha, nimetatakse statistiliseks kogumiks. Seda ei uurita tavaliselt kõik­võimalikest aspektidest vaid mingi (või mõne) tunnuse (omaduse) seisu­kohalt. Tunnuseks võivad olla näiteks inimeste pikkus, õpilaste hinne matemaatika eksamil, töötajate palk, rahvus, terade arv vilja­peas.

Tunnused liigituvad arvulisteks ja mitte­arvulisteks. Arvuline tunnus ehk arv­tunnus on tunnus, mille väärtusteks on arvud. Näiteks inimese pikkus, terade arv vilja­peas, palga suurus. Mitte­arvuline tunnus on tunnus, mille väärtusteks ei ole arvud. Näiteks rahvus, silmade värv.

Arvulised tunnused jaotatakse oma­korda kaheks: pidevateks ja diskreetseteks. Pidevaks tunnuseks nimetatakse tunnust, mis võib saada kõiki reaal­arvulisi väärtusi mingist piir­konnast. Sellised tunnused on näiteks keha­kaal, temperatuur. Diskreetseks tunnuseks nimetatakse tunnust, mis võib saada vaid üksikuid eraldi­seisvaid (tavaliselt täis­arvulisi) väärtusi. Sellised tunnused on näiteks seemnete arv vilja­peas, tähtede arv sõnas, lehe­külgede arv raamatus.

Diskreetse ja pideva tunnuse eristamine on mõneti tinglik. Pidevat tunnust (näiteks vanus) käsitletakse sageli diskreetsena (üldiselt mõõdetakse vanust täis­aastates).

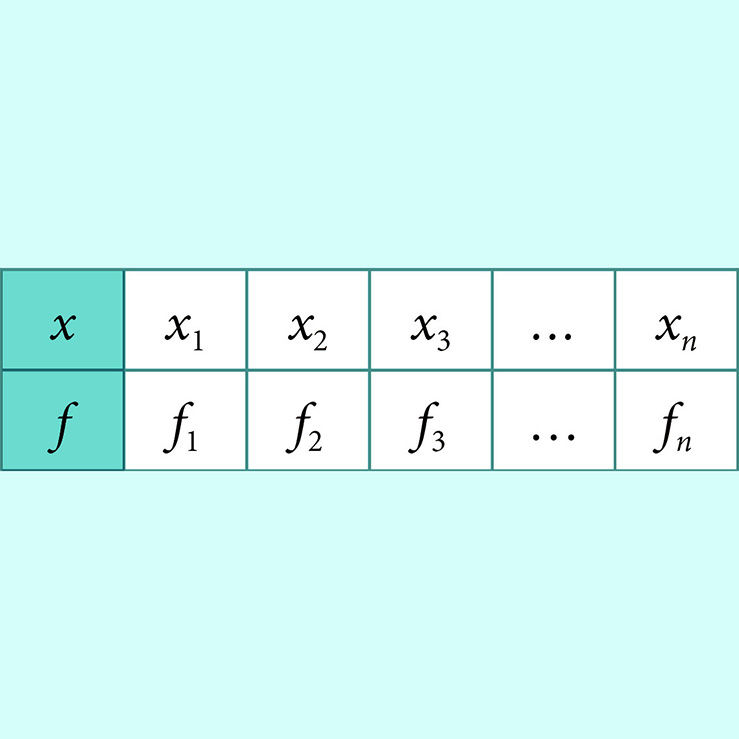
Tunnust, mille järgi vaadeldavat kogumit uuritakse, tähistatakse suur­tähega, tavaliselt X, Y, Z. Tunnuse suvalist väärtust (ka mitte­arvulise tunnuse korral) aga vastava väike­tähega x, y, z. Konkreetse väärtuse märkimiseks lisatakse väike­tähele indeks: x1, x2, …

Uuritava kogumi objektide mõõtmisel saadakse vaadeldava tunnuse väärtuste rida, nn statistiline rida:

a1, a2, a3, …, aN.

Igat arvu (väärtust) selles reas nimetatakse statistilise rea liikmeks. Tunnuse väärtuste arvu N nimetatakse kogumi mahuks või statistilise rea mahuks. Et statistiline rida ei ole üle­vaatlik (andmed esinevad reas mõõtmise järje­korras), siis on otstarbekas seda korrastada. Selleks kirjutatakse rea liikmed kas kasvavas või kahanevas järje­korras, kus­juures võrdsed liikmed kirjutatakse järjest. Tulemusena saadakse nn variatsioon­rida.

Näide 1.

Ühe klassi kontroll­töö hinnete variatsioon­rida oli järgmine:

2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5.

Siit on küll kerge leida hinnete vähimat väärtust (amin = 2) ja suurimat väärtust (amax = 5), kuid vähegi mahukama kogumi korral on andmete selline esitus ikka kohmakas, kas­või pikkuse pärast.

Variatsioon­reast parem on näite 1 andmete esitamine sagedus­tabelina, kus igale hindele (x) vastab tema esinemise arv ( f ):

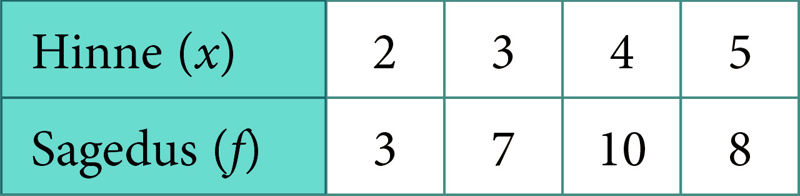
Tabelist saab kiirema üle­vaate hinnete jaotusest ning lihtne on leida, et kõige sagedamini esineb hinne 4. Ka kogumi mahu N saab kergesti: N = 3 + 7 + 10 + 8 = 28.

Sagedus­tabel esitatakse kas

horisontaalsena

või vertikaalsena.

Kogumi maht

N = f1 + f2 + f3 + … + fn.

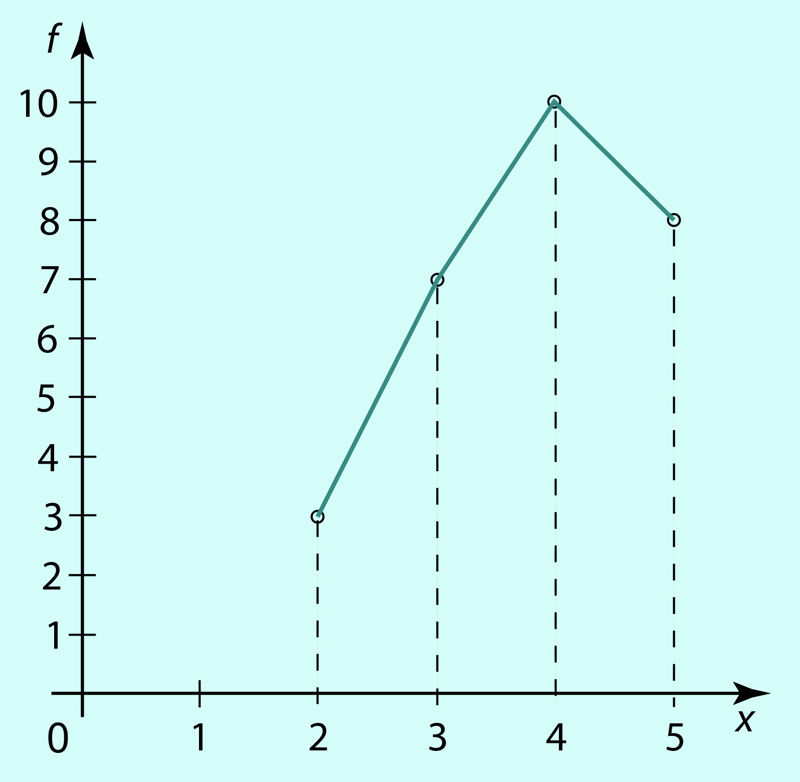
Parema üld­pildi saamiseks andmete muutumisest kujutatakse need geomeetriliselt sirg­lõik­diagrammina, mida nimetatakse sagedus­hulk­nurgaks (ka sagedus­murd­jooneks). Joonisel 1.17 on esitatud näite 1 andmetele vastav sagedus­hulk­nurk.

Joon. 1.17

Kahe kogumi võrdlemiseks mingi tunnuse järgi võrreldakse vastavaid sagedus­tabeleid või sagedus­hulk­nurki. Seda on aga tülikas teha ja see ei anna ka kiirelt õigeid järeldusi, kui kogumite mahud on erinevad.

Näide 2.

Järgnevas tabelis on esitatud sama kontroll­töö tulemused nii klassis A (näite 1 andmed) kui ka klassis B. Kummas klassis tehti töö paremini?

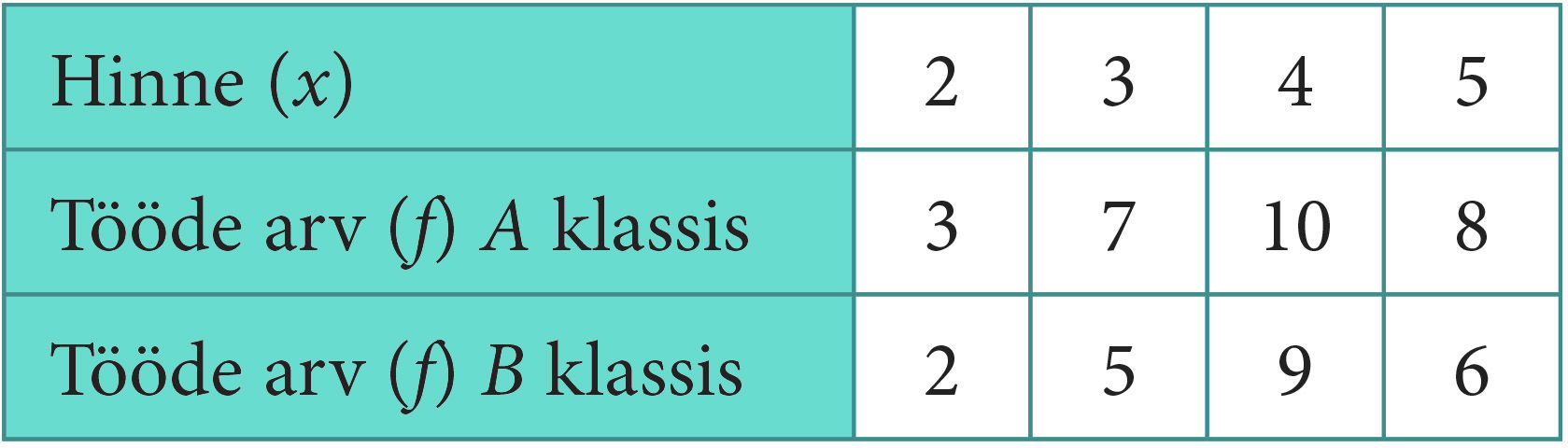
Andmeid on raske võrrelda, sest vastavad diagrammid (joon. 1.18) on küll sarnase kujuga, kuid ühel juhul oli kontroll­töö tegijaid 28, teisel juhul aga 22. Seega ei ole selge, milline on ühe või teise hinde osa­kaal vastava klassi kõigi hinnete seas.

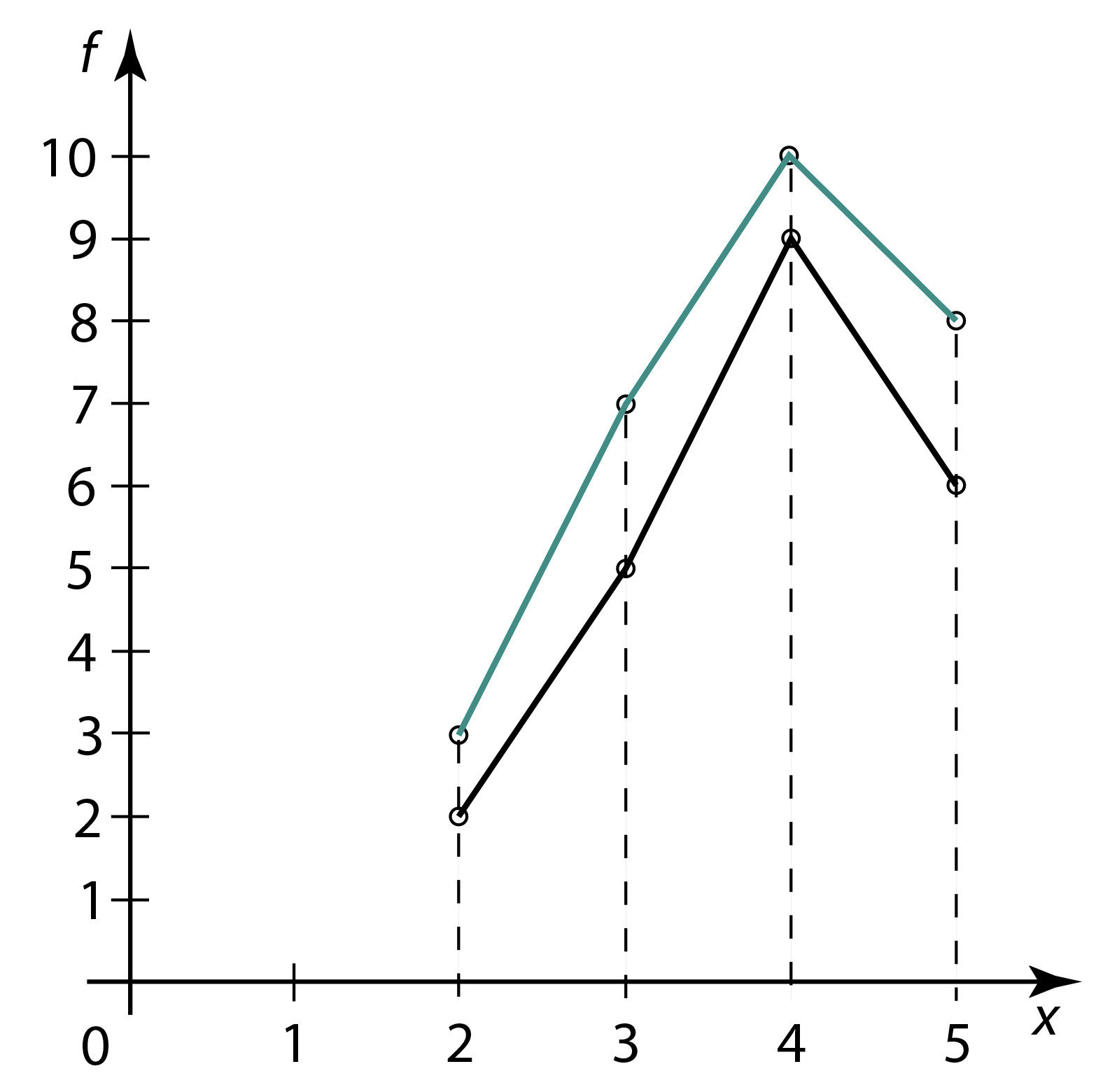Joon. 1.18

Erineva mahuga kogumite võrdlemiseks, nagu näite 2 korral, on ots­tarbekas kasutada sageduste asemel suhtelisi sagedusi. Suhteline sagedus antakse kas arvuna w_i=\frac{f_i}{N} \left(i=1,\ 2,\ \dots,\ n\right) või protsendina w_i\left(\%\right)=\frac{f_i}{N}\cdot100\%, i=1,\ 2,\ \dots,\ n, mis näitab, milline on tunnuse väärtuse xi osa­kaal kõigi väärtuste seas.

Tabelit, kus tunnuse väärtustele on seatud vastavusse nende esinemise suhteline sagedus, nimetatakse jaotus­tabeliks.

Üld­tähistuses on jaotus­tabel järgmine:

Seejuures on w1 + w2 + w3 + … + wn = 1, kui w_i=\frac{f_i}{N}, ja w1 + w2 + w3 + … + wn = 100%, kui w_i=\frac{f_i}{N}\cdot100\%.

Jaotus­tabelile vastavat sirg­lõik­diagrammi nimetatakse jaotus­hulk­nurgaks (ka jaotus­polügooniks).

Näide 3.

Tabelis on näites 2 esitatud hinnete sagedus­tabelite põhjal koostatud jaotus­tabelid. Joonisel 1.19 on vastavad jaotus­hulk­nurgad.

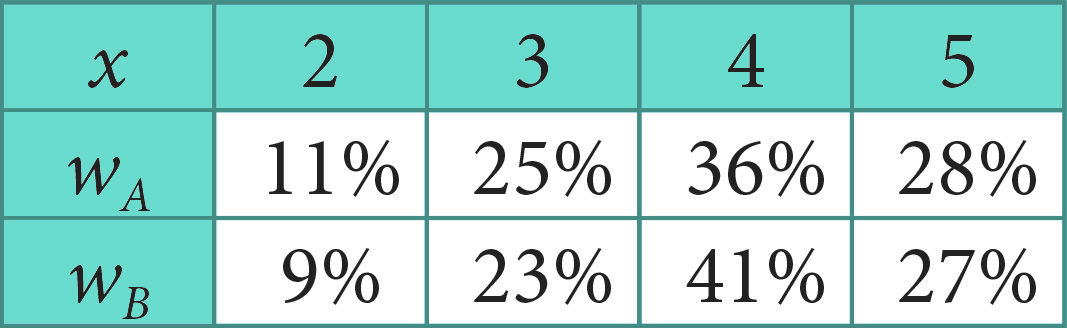
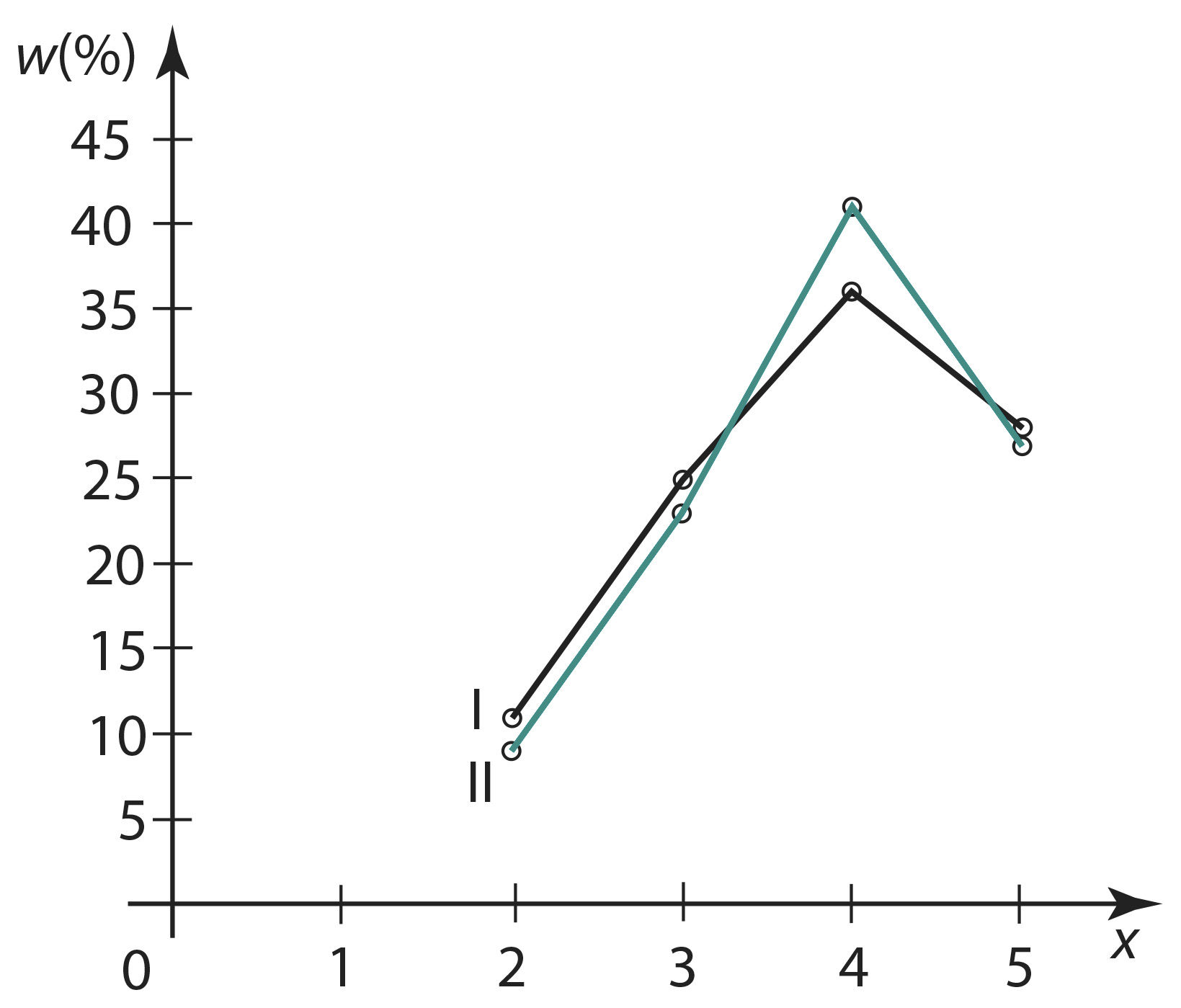Joon. 1.19

Nii tabeli kui ka joonise põhjal selgub, et B klassis on kontroll­töö tehtud mõne­võrra paremini: hinnete „2” ja „3” osa­kaal on vähenenud, veidi on vähenenud küll ka hinde „5” osa­kaal, kuid hinde „4” osa­kaal on oluliselt tõusnud. Öeldut kinnitab hinnete „4” ja „5” suhteliste sageduste summaarne võrdlemine: 64% ja 68%.

Kui kogumi tunnus on pidev või diskreetse tunnuse erinevaid väärtusi on väga palju, ei esitata andmete tabelis tunnuse üksikuid väärtusi, vaid väärtuste vahemikud ehk klassid. Nii saadakse rühmitatud sagedus- või jaotus­tabelid. Vahemike ots­punkte nimetatakse siis klassi­piirideks. Selline tabel on esitatud ülesandes 155.

Kui vahemike ots­punktid on tabelis esitatud nii, et kõigi vahemike esimesed ots­punktid on võrdsed eelmise vahemiku (nn madalama vahemiku) teise ots­punktiga, loetakse kahe vahemiku piiril olev arv madalamasse vahemikku kuuluvaks. Nii­sugune tabel on esitatud näites 4.

Tunnuse väärtuse vahemike arv sõltub uuritavast nähtusest ja uurimis­ees­märgist. Üks „jäme” reegel on järgmine: kui kogumi maht N pole väga suur, on sobiv vahemike arv umbes \sqrt{N}.

Näide 4.

Ühe klassi õpilaste pikkuste variatsioon­rida on järgmine: 156, 158, 159, 160, 160, 162, 163, 163, 163, 165, 165, 165, 166, 166, 167, 167, 167, 167, 168, 168, 168, 169, 170, 171, 171, 172, 173, 173, 173, 174, 174, 176, 184. Koostame vastava sagedus­tabeli ja jaotus­tabeli, kus tunnuse väärtused on esitatud vahemikes.

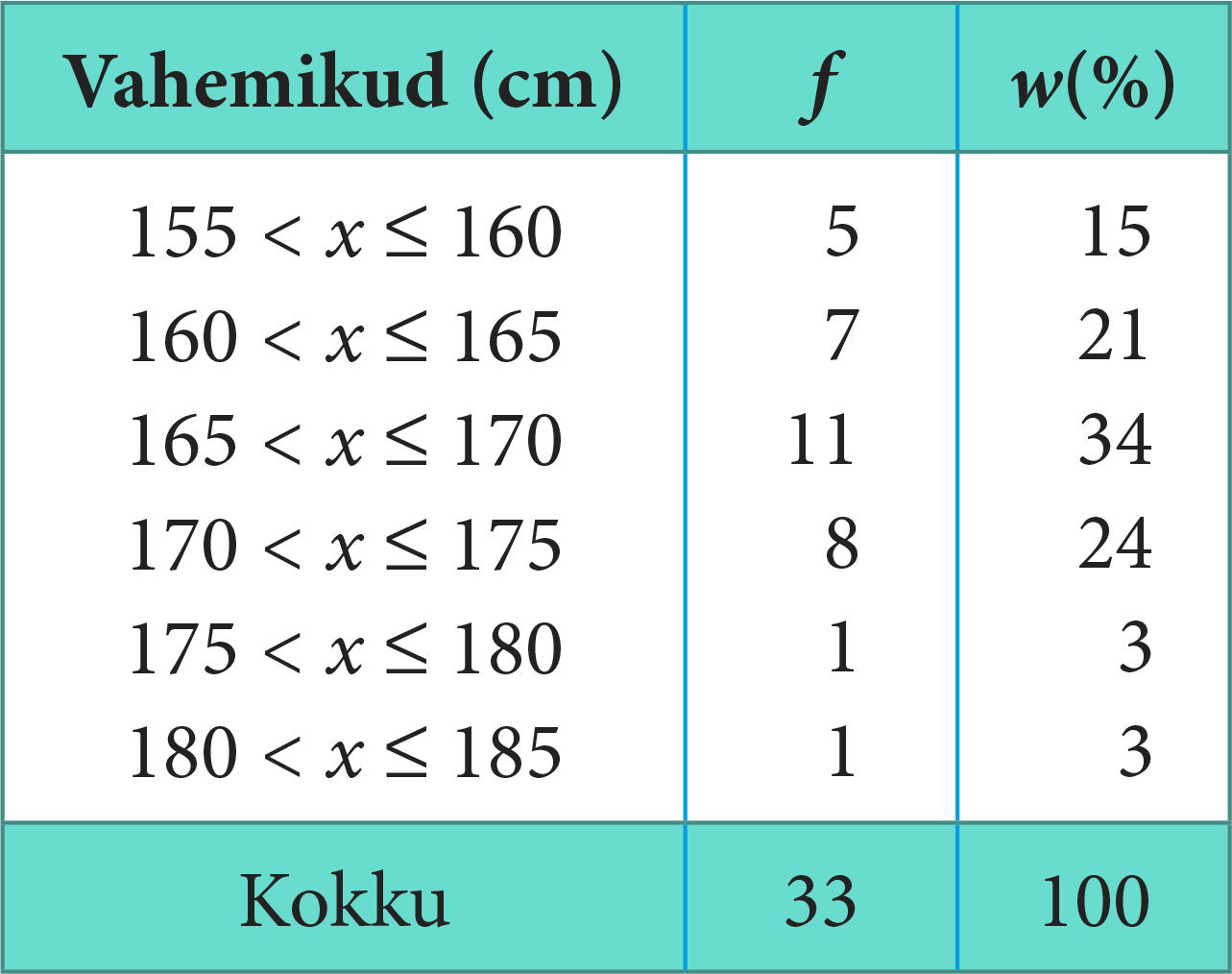Et N = 33 ja \sqrt{33}\approx5,7, siis sobiv vahemike arv on 6 või 5. Kuna ulatus xmax – xmin = 184 – 56 = 28 ei jagu vahemike arvuga 5 või 6 ja vahemike ots­punktideks eelistatakse täis­arve, võtame ulatuseks 30, mis annab vahemike arvu 6 korral vahemike pikkuseks 5 ühikut. Pikendanud ulatust 2 ühiku võrra, võtame esimese vahemiku alumiseks piiriks 155 ja viimase vahemiku ülemiseks piiriks 185. Nii saame järgmise tabeli:

Vahemikke võib märkida võrratusena nagu näites 4, kujul 155…160, 160…165 jne või kujul 155–160, 160–165 jne.

Kui sagedus- või jaotus­tabelis on tunnuse väärtused esitatud vahemikena, kujutatakse neid andmeid geomeetriliselt tulp­diagrammina, mida nimetatakse histogrammiks. Näite 4 jaotus­tabelile vastav histogramm on joonisel 1.20.

Joon. 1.20

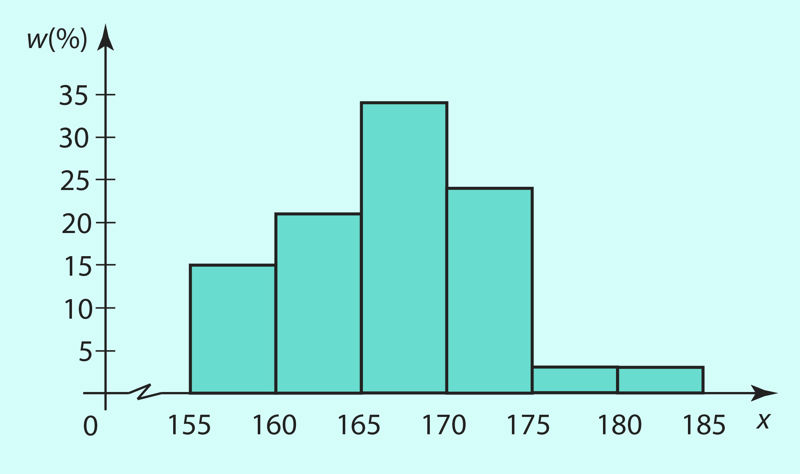
Otsmised vahemikud võivad olla ka lahtised, s.t esimese vahemiku alumine piir ja viimase vahemiku ülemine piir jäävad fikseerimata. Näite 4 puhul oleks siis esimene vahemik x ≤ 160 ja viimane vahemik 180 < x. Histogrammil jääb sel juhul esimene ja viimane vertikaal­lõik joonestamata.

Histogrammiga esitatakse tunnuse jaotus ka siis, kui tunnus on mitte­arvuline. Samuti sobib sel juhul hästi ka sektor­diagramm. Näiteks joonisel 1.21 on esitatud 1990. a Tartus sündinud laste sagedus­histogramm ja sektor­diagramm soo järgi.

Joon. 1.21
More like this
More options

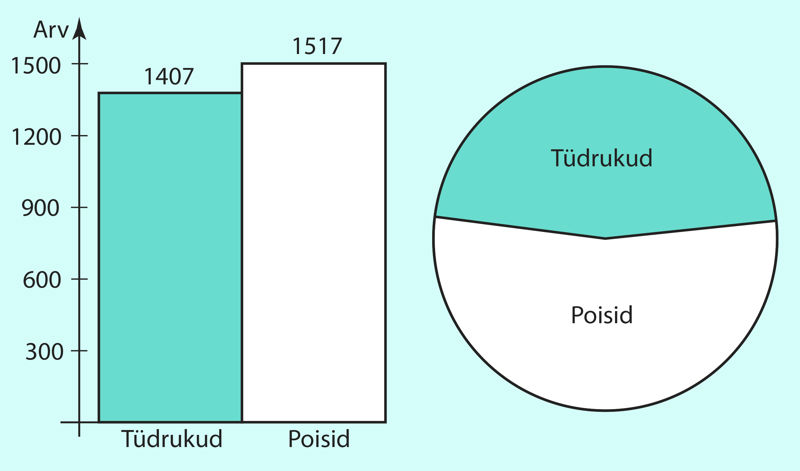
Ülesanded A

Ülesanne 149. Arvuline, mitte­arvuline, pidev ja diskreetne tunnus
        • kinganumber
        • haridus
        • vanus
        • kasv
        • sünniaasta
        • töötasu
        • nimi
        • sugu
        • töökoht
        Ülesanne 150. Kingade müümine
        • Arvuline
        • Mittearvuline
        • Pidev
        • Diskreetne

        Täitke vastav sagedus­tabel ja joonestage diagramm.

        Kinga number (x)

        38

        39

        40

        41

        42

        43

        44

        Sagedus (f)

        Milliseid kingi müüdi poes selle tunni jooksul kõige enam, milliseid kõige vähem?

        Vastus. Kõige enam müüdi number  kingi ja kõige vähem müüdi numbritega  ja  kingi.

        Ülesanne 151. Kinga­numbrid

        Vastus. Neidude kõige sagedamini esinev kinga­number on  ja noor­meestel . Meie klassi neidude kinga­number muutub st ni ja noor­meestel st ni.

        Ülesanne 152. Matemaatika kontroll­töö hinded

        Ülesanne 153. Õpilaste pikkused 5 klassina

        Vahemikud (cm)

        f

        w(%)

         < x ≤ 

         < x ≤ 

         < x ≤ 

         < x ≤ 

         < x ≤ 

        Kokku

        Ülesanne 154. Pikkuste jaotus­tabelid

        Vastus. Neidude pikkus muutub st ni ja noor­meestel st ni. Kõige sagedamini esinevate pikkuste vahemik on neidudel  ja noor­meestel .

        Ülesanne 155. Eesti rahvastik 2011. aastal
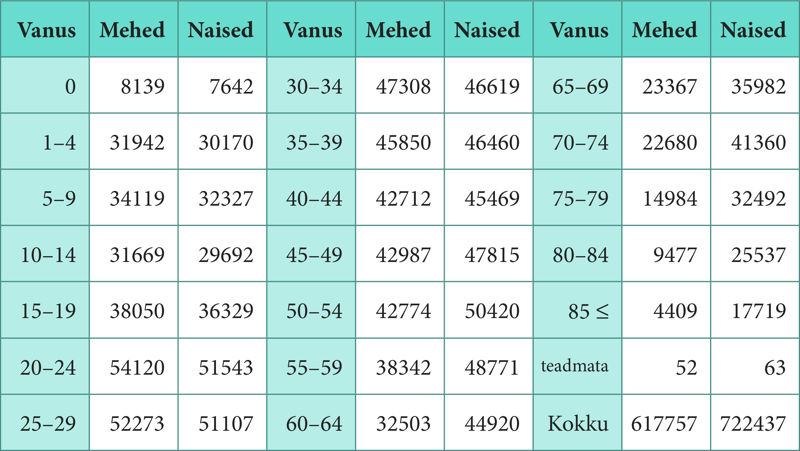
        1. Kui suur oli tõenäosus, et tänaval kohatav alla ühe aastane laps on poiss?
          Vastus. Tõenäosus, et tänaval kohatav alla ühe aastane laps on poiss, oli .
        2. Koostage jaotus­tabelid ja histogrammid (sobiv on seda teha arvuti abil) vanuse järgi naiste ning meeste kohta eraldi.
        3. Millises vanuses hakkas naiste arv ületama meeste arvu?
          Vastus. Naiste arv hakkas ületama meeste arvu vanuses .
        4. Mitu protsenti moodustasid alla aastased lapsed kogu rahvastikust?
          Vastus. Alla aastased lapsed moodustasid kogu rahvastikust %.
        5. Mitu protsenti rahvastikust oli 10 kuni 14 aasta vanuseid lapsi kokku, kuidas need jaotusid soo järgi?
          Vastus. 10 kuni 14 aasta vanuseid lapsi kokku oli kogu rahvastikust %. Neist % olid poisid ja % tüdrukud.
        6. Mitu protsenti oli pensionäre (alates vanusest 65) meeste ja naiste seas eraldi, kokku kogu rahvastikust?
          Vastus. Pensionäre oli % meestest ja % naistest ning kogu rahvastikust oli nende osa­kaal %.
        7. Mitu naist tuli ühe mehe kohta vanuses 20–29 aastat ja vanuses 30–39?
          Vastus. Vanuses 20–29 oli ühe mehe kohta  naist ja vanuses 30–39 oli ühe mehe kohta  naist.

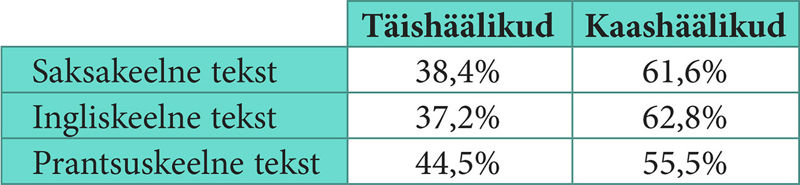
        Ülesanne 156. Täis- ja kaas­häälikute arv eesti­keelses tekstis

        Ülesanne 157. Eesti rahvuslik koosseis

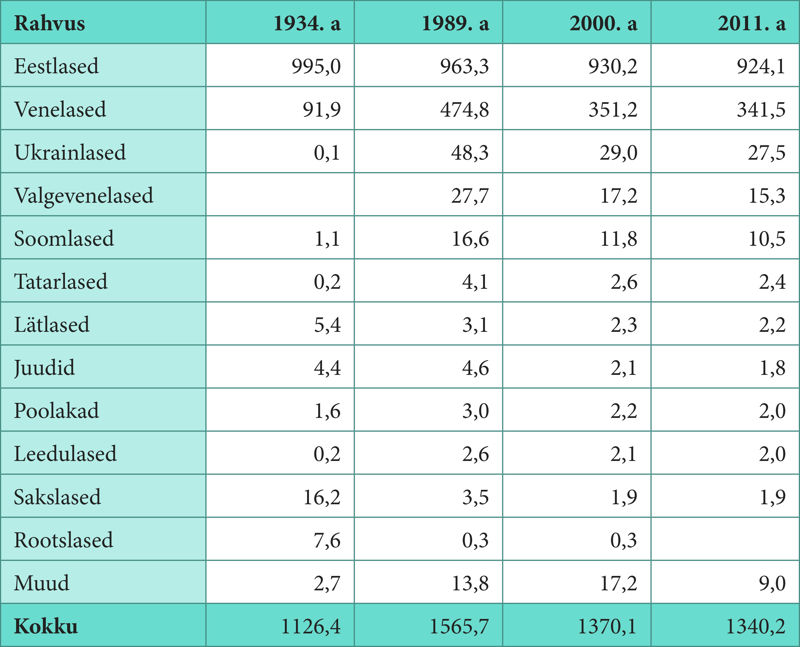
        1934. a

        1.  %
        2.  %
        3.  %
        4.  %
        5.  %

        1989. a

        1.  %
        2.  %
        3.  %
        4.  %
        5.  %

        2000. a

        1.  %
        2.  %
        3.  %
        4.  %
        5.  %

        2011. a

        1.  %
        2.  %
        3.  %
        4.  %
        5.  %
        More like this
        More options