Samasihiliste vektorite liitmine
Liitmisreegel
Kahe vektori liitmiseks rakendame teise vektori alguspunkti esimese lõpp-punkti ning võtame summaarseks vektoriks esimese vektori alguspunktist teise vektori lõpp-punkti viiva vektori.
Näide 1
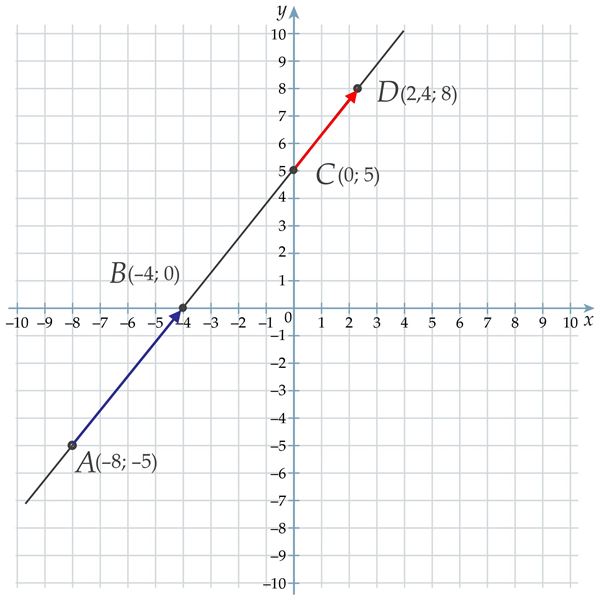
A(3; 11), B(0,5; 1) ja C(–1; –5). Need punktid asuvad sirgel y = 4x – 1. Veendume, et + = .
- = (–2,5; –10),
- = (–1,5; –6),
- = (–4; –16).
Seega nihe x-telje sihis on –2,5+(–1,5) ja nihe y-telje sihis on –10+(–16) ning vektor
= (–2,5 –1,5; –10 –16) ⇒
= (–4; –16).
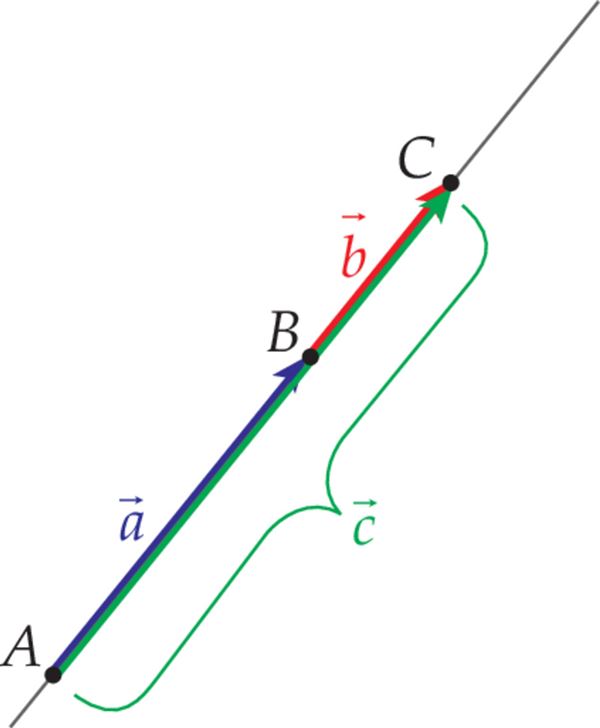
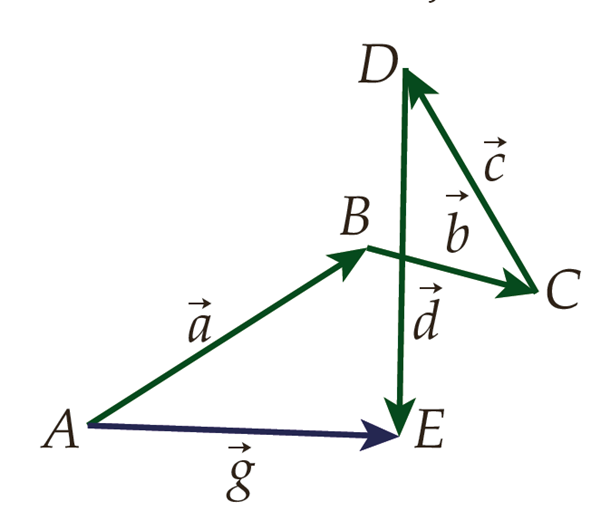
Kolmnurga reegel
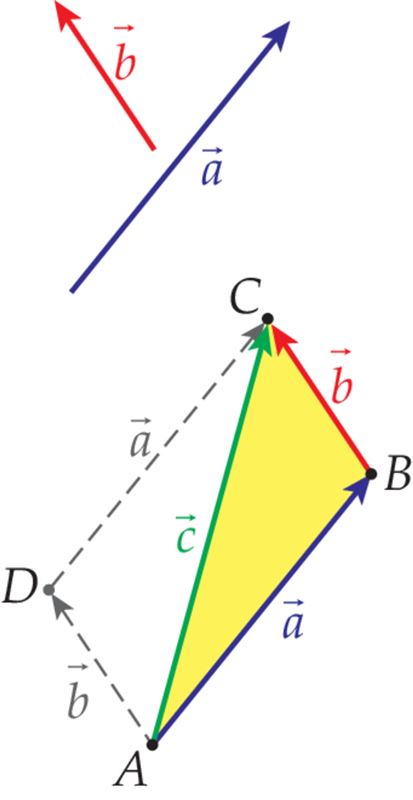
Vaatleme nüüd mis tahes kahe vektori ja summat. Ka sel juhul alustame liikumist esimese vektori suunas kuni selle lõpuni ja jätkame sealt teise vektori suunas selle pikkuse võrra.
Vektori abil liigume punktist A punkti B ja jätkame sealt liikumist vektori suunas punktini C. Seega, summaarne nihe, mis vastab vektorite summale, on punktist A punkti C. Järelikult on vektor vektorite summa.
Märka
Vektorite summa ei muutu, kui liidetavate järjekorda vahetada. Vektori suunas jõuame punktist A punkti D ja sealt vektori suunas punkti C. Tulemuseks on sama vektor
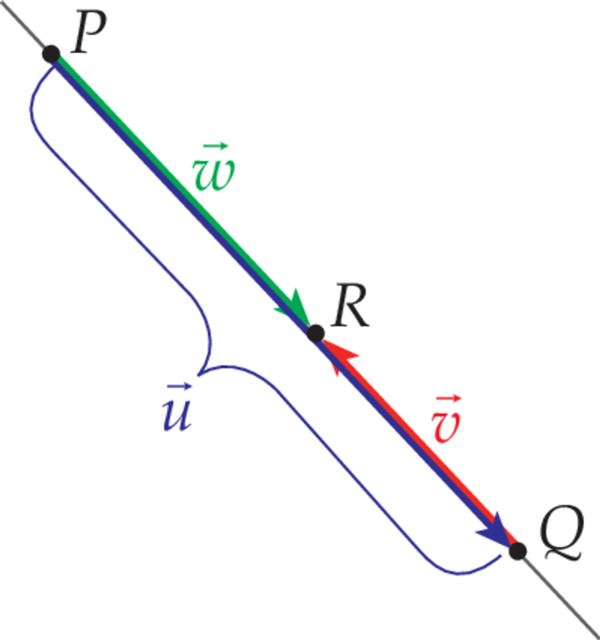
Kolmnurgareegel
Kahe vektori liitmiseks rakendame teise vektori alguspunkti esimese lõpp-punkti ning võtame summaarseks vektoriks esimese vektori alguspunktist teise vektori lõpp-punkti viiva vektori.
Selgitused
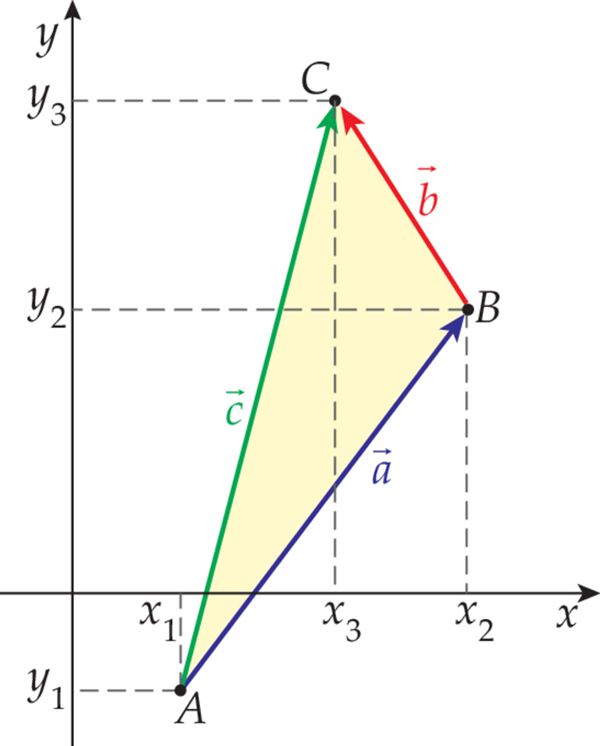
Leiame summaarse vektori koordinaadid. Olgu liidetavate vektorite koordinaadid
=(a1; a2) ja =(b1; b2).
Vektorite koordinaadid avalduvad punktide koordinaatide kaudu.
a1 = x2 – x1
a2 = y2 – y1
b1 = x3 – x2
b2 = y3 – y2
Kui liikuda vektori suunas ja siis vektori b suunas, on muutuja x summaarne muut
x2 – x1 + x3 – x2 = x3 – x1.
Analoogselt on muutuja y summaarne muut
y2 – y1 + y3 – y2 = y3 – y1.
Saadud muudud ongi vektori koordinaadid, järelikult
= (x3 – x1; y3 – y1) = (a1 + b1; a2 + b2) =
(;)
(;)
(;)
(;)
Vektorite summa koordinaadid võrduvad liidetavate vektorite vastavate koordinaatide summaga.
Hulknurgareegel
Kolmnurga reeglit saab üldistada rohkem kui kahe vektori geomeetriliseks liitmiseks. Tulemuseks on hulknurgareegel.
On vaja liita kolm või rohkem vektorit. Rakendame teise vektori alguse esimese vektori lõppu, kolmanda vektori alguse teise vektori lõppu jne. Vektorite summaks on vektor, mis viib esimese vektori alguspunktist viimase vektori lõpp-punkti.
Näide 2
Liigutades vektoreid liugurite abil veendu, et sõltumata liidetavate järjekorrast on summavektor sama.
Märka
Kui pärast vektorite paigutamist vastavalt hulknurgareeglile langeb viimase vektori lõpp-punkt kokku esimese vektori alguspunktiga, siis on kõigi vektorite summaks nullvektor, st vektorite summa on null.
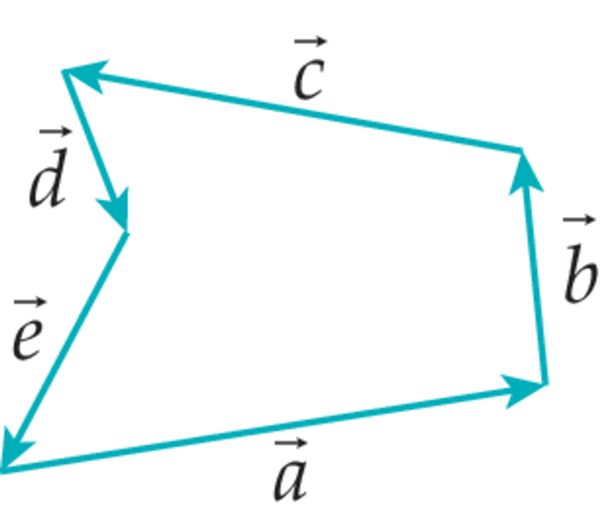
++++=
Summavektor on .
Olgu liidetavate vektorite koordinaadid järgmised:
(–2; 4), (0; –6), (3; –1), (4; 3).
Summavektori koordinaadid on = (; ).
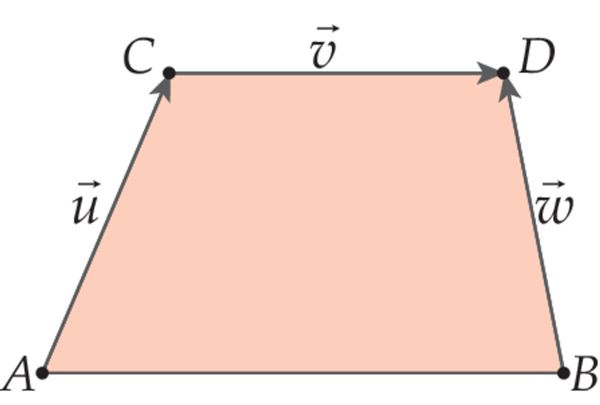
Rööpkülikureegel
Et nelinurga ABCD vastasküljed on paralleelsed ja võrdsed, siis on tegemist rööpkülikuga. Siit tuleneb vektorite liitmise rööpkülikureegel.
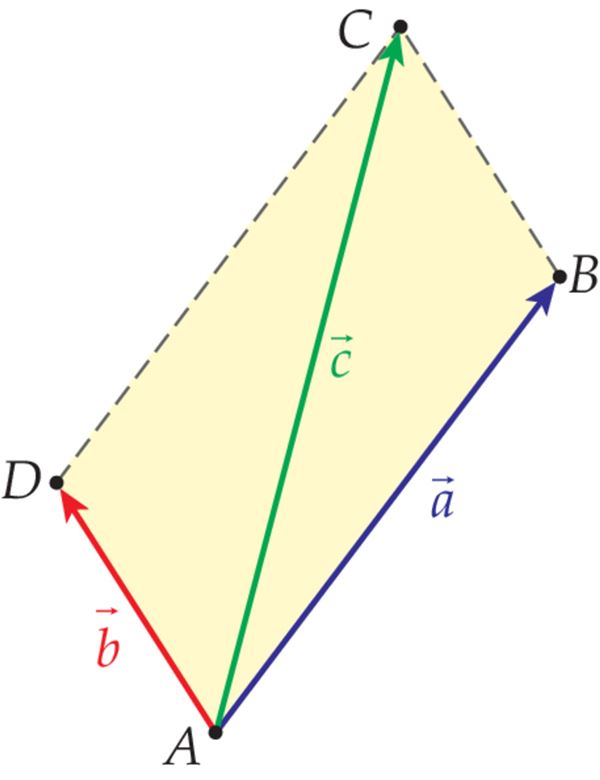
Kahe vektori liitmiseks rakendame nende algused samasse punkti ja moodustame rööpküliku, mille külgedeks on need vektorid. Summaks on vektor, mis väljub ühisest algpunktist, paikneb rööpküliku diagonaalil ja on sama pikk kui diagonaal.
Märka
Rööpküliku reegel sisaldab vektorite liitmise kolmnurgareeglit.
= ja
=
Harjuta ja treeni
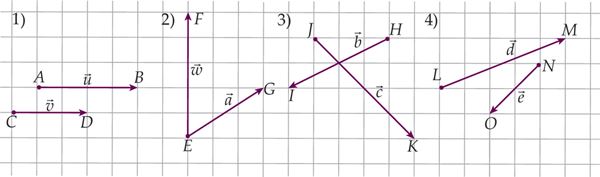
++
++
Masinas toimub andmete konventeerimine vastavalt skeemile ja vektorite liitmise reeglitele.
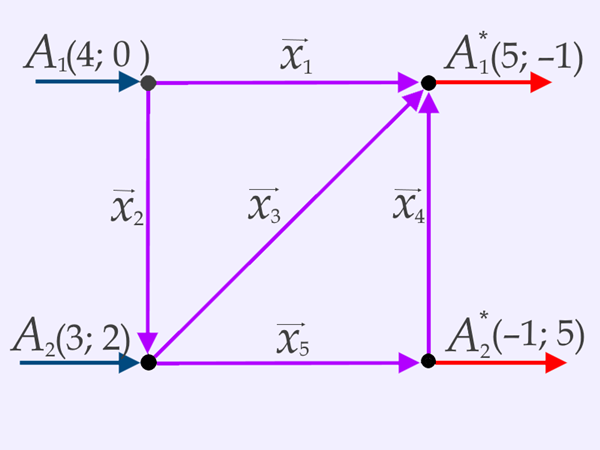
(; )
(; )
(; )
(; )
(; )
Masinas toimub andmete konventeerimine vastavalt skeemile ja vektorite liitmise reeglitele.
- (; )
- (; )
- (; )
- (; )
- (; )
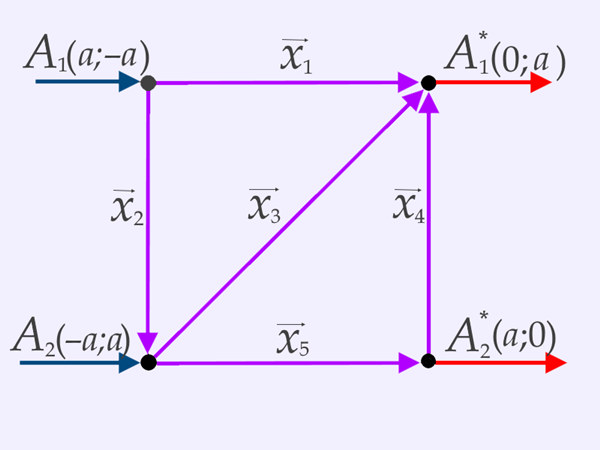
- A1(a; –a) – – – A3*(a; a)
- A1(–a; a) – – – A3*(a; a)