Vaatleme katset, mida saab korrata kui tahes palju kordi, kusjuures iga katse tulemuseks on mingi arv (n erineva võimaliku arvu seast). Näiteks täringu viskamisel on võimalikeks tulemusteks silmade arvud. Katsetulemusi saame vaadelda ka ühe muutuja X võimalike väärtustena x1, x2, …, xn. Et juhus määrab, milline väärtus parajasti esile tuleb, nimetatakse muutujat X juhuslikuks suuruseks.
Juhusliku suuruse iga võimalik väärtus on omakorda vaadeldav juhusliku sündmusena. Juhuslikuks sündmuseks võivad aga olla ka juhusliku suuruse X nende väärtuste esiletulekud, mis rahuldavad tingimust a < X < b või X < c jne.
Näide 1.
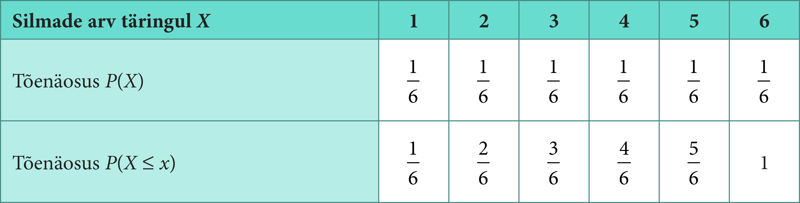
Olgu katseks täringuvise. Katse võimalikeks tulemusteks on 1, 2, 3, 4, 5 või 6 silma. Need on juhusliku suuruse X (täringul tulnud silmade arv) väärtused: x1 = 1, x2 = 2, x3 = 3, x4 = 4, x5 = 5, x6 = 6, millest igat võib vaadelda juhusliku sündmusena: E1 ühe silma tulek, E2 kahe silma tulek jne. Loeme sündmuseks A aga silmade arvu X ≤ 4 tulekut.
Näide 2.
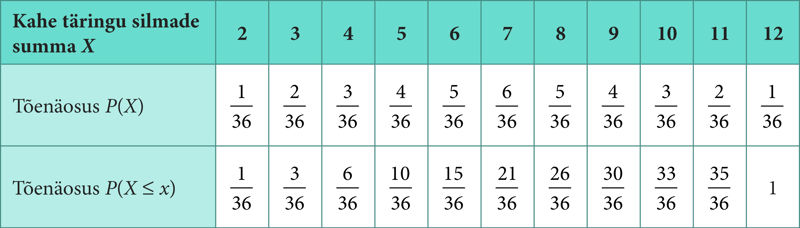
Olgu juhuslikuks suuruseks X kahe täringu korraga viskamisel tulev silmade summa. Suuruse X võimalikud väärtused on arvud 2, 3, 4, …, 12.
Juhusliku suuruse X iga väärtuse xi korral on võimalik leida selle esinemise tõenäosus pi, sest väärtuse xi tulek on teatud juhuslik sündmus. Tulemused võime põhimõtteliselt esitada arvupaaridena (xi; pi), tabelina, graafikuna ja ka valemina. Need on aga funktsiooni võimalikud esitusviisid. Seetõttu öeldaksegi, et vastavuse juhusliku suuruse X võimalike väärtuste ja tõenäosuste vahel korraldab tõenäosusfunktsioon. Definitsioonina:
juhusliku suuruse X tõenäosusfunktsiooniks nimetatakse eeskirja, mis seab juhusliku suuruse X igale võimalikule väärtusele xi vastavusse selle väärtuse esiletuleku tõenäosuse pi (ehk P(xi)).
Kui juhusliku suuruse tõenäosusfunktsioon on leitud, öeldakse ka, et leitud on juhusliku suuruse jaotus.
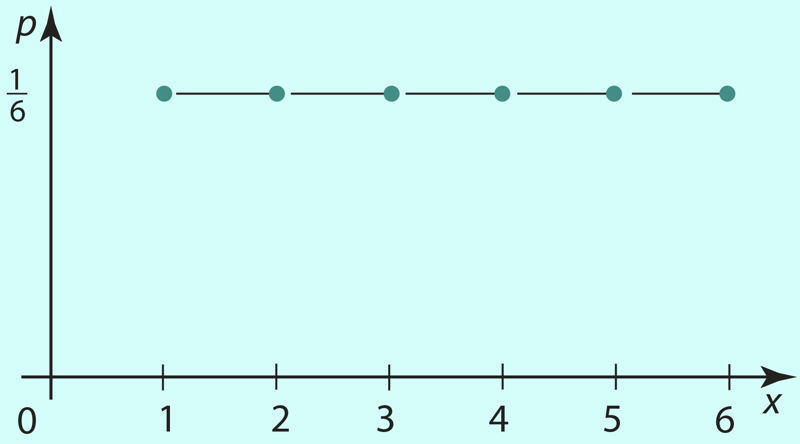
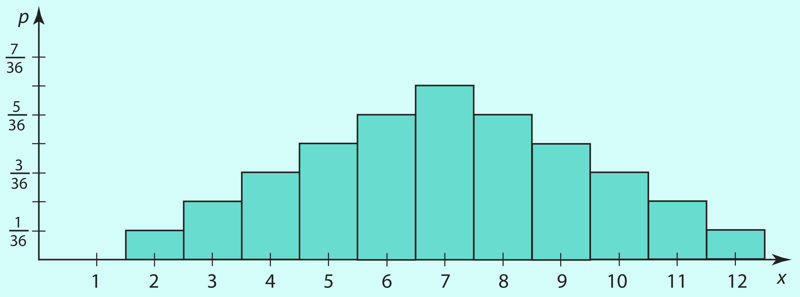
Järgmise kahe tabeli esimese ja teise reaga on esitatud näidetes 1 ja 2 kirjeldatud juhuslike suuruste jaotused. Vastavad graafilised esitused on joonistel 1.29 ja 1.30.
Kui on antud juhusliku suuruse jaotus, s.t arvupaarid (xi; pi), kus i = 1, 2, .., n, siis kehtib tõenäosusfunktsiooni põhiomadus
p1 + p2 + … + pn = 1,
sest igal katsel mingi väärtus xi kõikvõimalike väärtuste x1, x2,…, xn seast ikka esile tuleb (vastavate sündmuste summa on ju kindel sündmus).
Juhusliku suuruse X jaotus esitatakse sageli ka funktsiooniga P(X ≤ x), mida nimetatakse tõenäosuse jaotusfunktsiooniks. See funktsioon seab suuruse X igale väärtusele xi vastavusse tõenäosuse P(X ≤ xi), s.t tõenäosuse, et juhusliku suuruse X väärtus ei ole suurem kui xi.
Näidetele 1 ja 2 vastavad jaotusfunktsioonid on esitatud eelmiste tabelite esimese ja kolmanda reaga. Näite 1 korral on tõenäosuse jaotusfunktsiooni graafik joonisel 1.31.
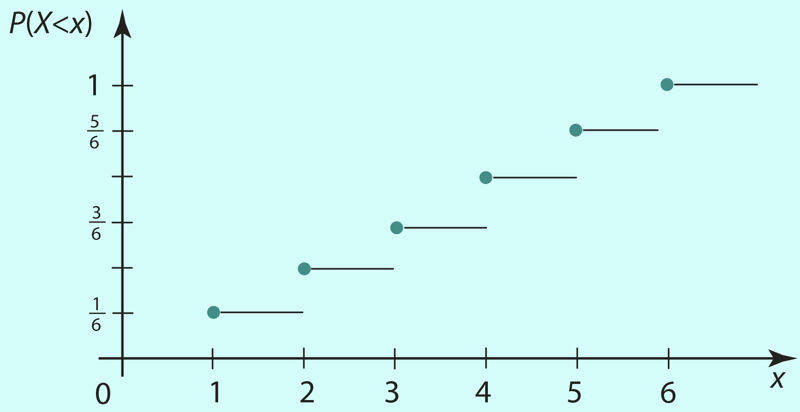
Lahendame tõenäosusfunktsiooni ja jaotusfunktsiooni kohta täringuvisete korral mõned ülesanded.
Näide 3.
Leiame tõenäosuse, et täringu viskamisel tuleb kas 1, 4 või 6 silma:
P (kas 1 või 4 või 6) = P(1) + P(4) + P(6) =
Näide 4.
Leiame tõenäosuse, et visates korraga kaht täringut tuleb 1) mitte rohkem kui 5 silma, 2) mitte vähem kui 5 silma, kuid mitte rohkem kui 8 silma.
- Leiame vastuse nii a) tõenäosusfunktsiooni P(x) kui ka b) jaotusfunktsiooni P(X ≤ x) tabeli abil:
- P(X ≤ 5) = P(kas 2, 3, 4 või 5) = P(2) + P(3) + P(4) + P(5) =
\frac{1}{36}+\frac{2}{36}+\frac{3}{36}+\frac{4}{36} =\frac{10}{36} =\frac{5}{18} ≈ 0,28; - P(X ≤ 5) =
\frac{10}{36} ≈ 0,28.
- P(X ≤ 5) = P(kas 2, 3, 4 või 5) = P(2) + P(3) + P(4) + P(5) =
- P(5 ≤ X ≤ 8) = P(5) + P(6) + P(7) + P(8) =
\frac{4}{36}+\frac{5}{36}+\frac{6}{36}+\frac{5}{36} =\frac{20}{36} =\frac{5}{9} ≈ 0,56 või P(5 ≤ X ≤ 8) = P(4 < X ≤ 8) = P(X ≤ 8) – P(X ≤ 4) =\frac{26}{36}-\frac{6}{36} =\frac{20}{36} ≈ 0,56.
Käesoleva teema peatükides 1.10–1.12 vaatlesime statistilise kogumi uurimist mingi arvtunnuse seisukohalt. Seal esinenud arvtunnus on sisuliselt juhuslik suurus, mis on määratud jaotustabeliga, kus iga väärtuse tõenäosuseks on tema suhteline sagedus. Tunnuse (kui juhusliku suuruse) jaotus saadi katsete ja vaatluste teel, s.t empiiriliselt; käesolevas peatükis vaadeldud juhuslike suuruste (näide 1 ja 2) jaotuse saime teoreetilise kaalutluse abil. Juhuslikke suurusi (ja nende jaotusi) võib defineerida ka teoreetiliselt ning vaadelda neid siis kui mudeleid teatud empiirilistele jaotustele. Nii võib näidete 1 ja 2 andmetel esitatud juhuslike suuruste jaotusi vaadelda kui teoreetilisi mudeleid vastavatele täringuvisete tegelikele katsetele.
Ülesanded A
Ülesanne 196. Kaheteisttahuline täring
 Joon. 1.32 | ||||||
X | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
P(X) |
Ülesanne 197. Kaheteisttahuline täring
P(X) | |
paarisarv silmi? | |
algarv silmi? | |
7 kuni 10 silma? | |
vähemalt 9 silma? |
Ülesanne 198. Loterii
Vastus. Tõenäosus võita on
Ülesanne 199. Täringu viskamine
Ülesanne 200. Raha jagamine
Ülesanne 201. Õnneratas
Vastus. 1)
