Korrelatsiooni­tabel

Joon. 1.26

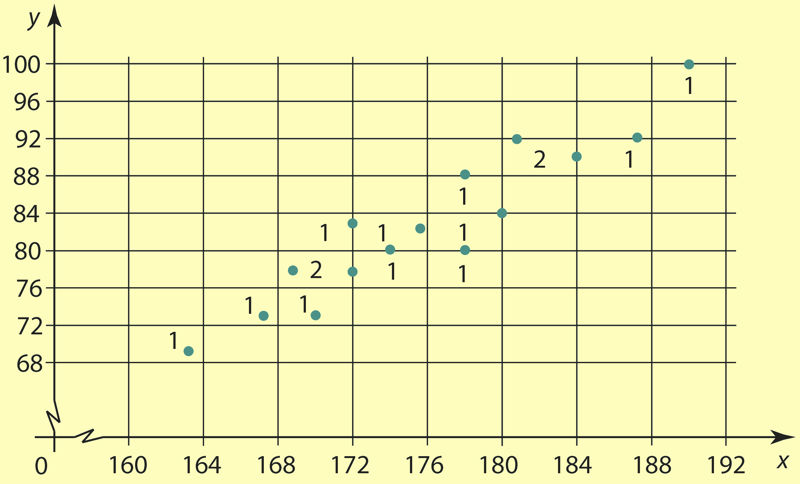
Vaatleme eelmise pea­tüki näitele vastavat korrelatsiooni­välja, mis on esitatud joonisel 1.23. Paneme sellele väljale (joon.1.26) võrgustiku (ruudustiku). Sisuliselt jaotame tunnuste X ja Y väärtused klassideks. Loeme, mitu punkti satub igasse rist­külikusse, arvestades, et vahemikeks jaotamise korral loetakse kahe vahemiku piiril olev väärtus madalamasse vahemikku kuuluvaks. Loendamise tulemusi märgivad joonisel 1.26 tabeli lahtrites olevad arvud. Kandes need koos tunnuste väärtuste vahemikega või vahemike esindajatega (kui andmetega jätkatakse arvutusi) tabelisse, saame nn korrelatsiooni­tabeli.

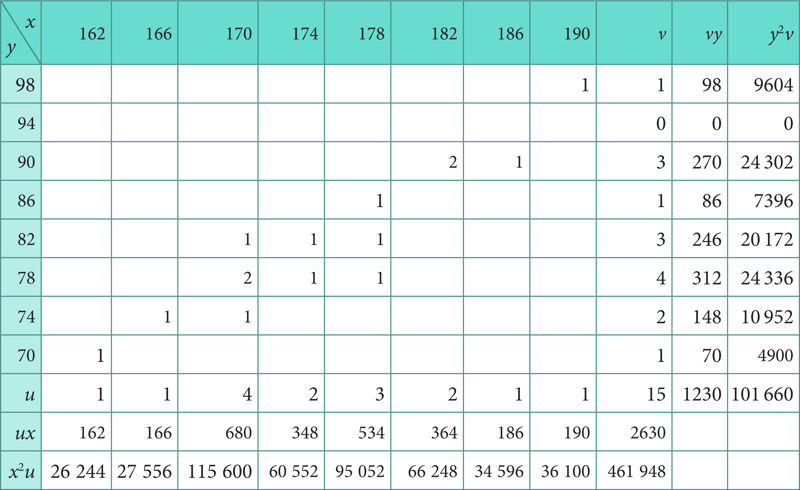
Korrelatsiooni­tabel koostatakse tavaliselt korrelatsiooni­välja kasutamata. Selleks jaotame X ja Y muutumis­piirkonna sobivalt vahemikeks (klassideks), kirjutame need või vahemike esindajad tabeli esimesse ritta ja esimesse veergu (või vastu­pidi) ning märgime tekkinud ruudustikku kriipsukesena iga konkreetse arvu­paari. Hiljem loeme kriipsukesed igas kastis kokku ja kirjutame sinna saadud sageduse.

Edasiste arvutuste hõlbustamiseks on ots­tarbekas lisada korrelatsiooni­tabelile üks rida (u) ja üks veerg (v), kuhu kirjutatakse vastavalt veergudes ja ridades olevate sageduste summad. Nüüd moodustab esimene veerg koos veeruga v kogumi sagedus­tabeli tunnuse Y järgi ning esimene rida koos reaga u kogumi sagedus­tabeli tunnuse X järgi.

Kui korrelatsiooni­tabelis asendada arvu­paaride esinemise sagedused suhteliste sagedustega, saadakse uuritava kogumi jaotus kahe tunnuse järgi.

Üldiselt esitatakse korrelatsiooni­tabeliga statistilisi andmeid siis, kui erinevaid arvu­paare (xi ; yi) on väga palju ja tunnuste väärtusi on ots­tarbekas jaotada vahemikeks või kui täpselt ühe­suguseid arvu­paare on palju. Meie näite puhul pole tegemist kummagi juhuga ja piisaks eelmise artikli näites esitatud tabelist. See­tõttu tuleb siin esitatut vaadelda kui illustratsiooni keerulisemate juhtude jaoks.

Näide.

Leiame saadud korrelatsiooni­tabeli andmetel tunnuste X ja Y väärtuste aritmeetilise keskmise (\overline{x} ja \overline{y}) ning standard­hälbe (σx ja σy).

Kui arvutusi teha kirjalikult, on ots­tarbekas lisada korrelatsiooni­tabelile veel ridu ja veerge; meie näite korral on lisatud ux ja x2u väärtuste rida ning vy ja y2v väärtuste veerg, kuhu on kantud ka vastavad summad.

Nüüd:

\overline{x}=\frac{2630}{15}\approx175,33\ \mathrm{\left(cm\right)}, \overline{y}=\frac{1230}{15}\approx82,00\ \mathrm{\left(kg\right)},

σx2 = \overline{x^2}-\overline{x}^2 = \frac{461948}{15}-175,33^2\approx55,924 ⇒ σx ≈ 7,48 cm,

σy2 = \overline{y^2}-\overline{y}^2 =\frac{101660}{15}-82^2\approx53,333 ⇒ σy ≈ 7,30 kg.

Korrelatsiooni­väli ja korrelatsiooni­tabel (näiteks joonisel 1.23 esitatud korrelatsiooni­väli ja sellele vastav tabel peatüki 1.15 näites) esitavad tunnuste X ja Y väärtuste x ja y vahelist seost. See seos ei ole aga funktsionaalne seos, sest ühe muutuja igale võimalikule väärtusele ei vasta mitte üks, vaid sageli mitu teise muutuja väärtust. Ja mis veel oluline on: ühe muutuja fikseeritud väärtusele vastab teise suuruse üks või mitu erinevat juhusest sõltuvat väärtust. Nii näiteks vastab meie näite korral mehe pikkusele 163 cm vaid keha­kaal 69 kg, kuid pikkusele 172 cm keha­kaalud 78 kg ja 83 kg. Et keha­kaalu väärtused just sellised on, on juhus. Kirjeldatud sõltuvust tunnuste X ja Y väärtuste x ja y vahel nimetatakse statistiliseks ehk stohhastiliseks sõltuvuseks. Lühemalt:

statistiliseks sõltuvuseks kahe juhusliku muutuja (suuruse) vahel nimetatakse vastavust, kus ühe muutuja igale võimalikule väärtusele vastab teise muutuja võimalik jaotus.

More like this
More options

Ülesanded B

Ülesanne 191. Korrelatsiooni­tabel tunnustega pikkus ja kaal

Ülesanne 192. Matemaatika ja füüsika kontroll­tööde hinded

More like this
More options