Eksponentfunktsioon

Peatükis 3.2 selgus, et suuruste liitprotsendiline kasvamine või kahanemine väljendub funktsioonina y = ca^x, kus 0 < a < 1 või a > 1 ning x ∈ N. Vaatleme nüüd funktsiooni y = ca^x, kus x ∈ R, a ∈ R⁺, a ≠ 1, c ∈ R.

Funktsiooni y = ca^x, kus a > 0, a ≠ 1, x ∈ R, nimetatakse eksponentfunktsiooniks.

Näide 1.

Funktsioonid y = 2^x, y = 0,6^x, y = 2,34^x, y = 5 · 0,9^x, y=-4\cdot\left(\frac{4}{7}\right)^x on eksponentfunktsioonid.

Edaspidi piirdume põhiliselt funktsioonidega kujul y = a^x.

Eksponentfunktsiooni määramispiirkonnaks on kogu reaalarvude hulk R,s.t –∞ < x < +∞.

Vaatleme eksponentfunktsiooni y = a^x .

1. Eksponentfunktsiooni positiivsuspiirkond ühtib tema määramispiirkonnaga R, negatiivsuspiirkond puudub.

See on tõepoolest nii, sest positiivse arvu a aste a^x on alati positiivne.

2. Eksponentfunktsioonil puuduvad nullkohad.

Nimetatud omadus järeldub otseselt eelnevast omadusest.

3. Eksponentfunktsiooni graafik läbib punkti A(0; 1).

Tõepoolest, kui x = 0, siis y = a⁰ = 1.

4. Eksponentfunktsiooni graafik läbib punkti B(1; a).

Tõepoolest, kui x = 1, siis y = a¹ = a.

5. Kui a > 1, siis eksponentfunktsioon on kasvav;kui 0 < a < 1, siis eksponentfunktsioon on kahanev.

See omadus järeldub peatükis 3.1 esitatud teoreemist: kui r₁ < r₂ (r₁, r₂ ∈ R), siis a > 1 korral on a^{r_1}<a^{r_2}, 0 < a < 1 korral aga a^{r_1}>a^{r_2}.

6.1. Kui a > 1, siis argumendi x (x ∈ R) väärtuste tõkestamatul kasvamisel kasvavad ka funktsiooni y = a^x väärtused tõkestamatult.

Öeldu järeldub omadusest 5 ja sellest, et jada, mille üldliige on aⁿ (a > 1, n ∈ N), väärtused kasvavad kui tahes suureks.Olgu a > 1. Kui x < 0, siis saab selle kirjutada kujul x=-\left|x\right|. Järelikult funktsiooni y = a^x võime kirjutada kujul y=a^{-\left|x\right|} ehk y=\frac{1}{a^{\left|x\right|}}. Kui nüüd x → –∞ ehk –|x| → –∞, siis |x| → ∞ ja \frac{1}{a^{\left|x\right|}}\to0 ehk a^–|x| → 0 ehk a^x → 0. Lühemalt: kui a > 1 ja x → –∞, siis y → 0. Seega,

liikudes piki x-telge vasakule (x → –∞) läheneb funktsiooni y = a^x graafik a > 1 korral pidevalt x-teljele. Seejuures ei lõika graafik kusagil x-telge.

Näide 2. Kui y = 5^x, siis andes argumendile x järjest väiksemaid (ka negatiivseid) väärtusi, saame järjest väiksemad funktsiooni väärtused: kui x on 2; –3; –8, on 5^x väärtused 25; 0,008; 0,00000256.

Sirget, millele funktsiooni graafik (joon) tõkestamatult läheneb, kui graafiku (joone) punkt tõkestamatult kaugeneb koordinaatide alguspunktist, nimetatakse selle funktsiooni graafiku (joone) . Seega on funktsiooni y = a^x, kus a > 1, graafiku x-telg.

Arvestades eksponentfunktsiooni omadusi 1–6 saame skitseerida y = a^x, a > 1 graafiku (joonis 3.2). See osutub pidevaks jooneks, s.t jooneks, mida saab joonestada kirjutusvahendit paberilt tõstmata. Seda öeldakse ka teisiti: eksponentfunktsioon y = a^x, a > 1 on pidev funktsioon.

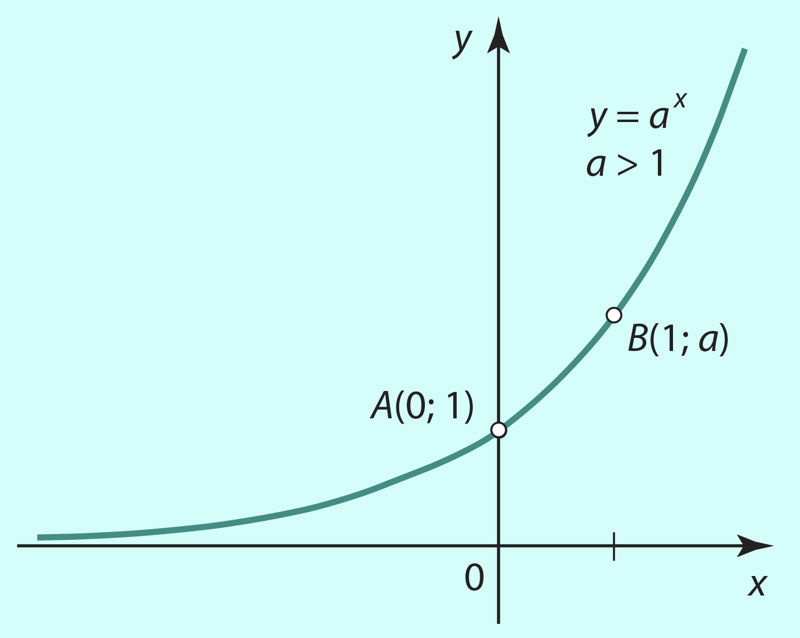Joon. 3.2

Eksponentfunktsiooni y = a^x, a > 1 muutumispiirkond Y = R⁺.

Omadus 6 on eksponentfunktsiooni y = a^x, 0 < a < 1 korral järgmine.

6.2. Kui 0 < a < 1, siis argumendi x väärtuste tõkestamatul kasvamisel funktsiooni y = a^x väärtused vähenevad ja lähenevad tõkestamatult nullile.

Öeldu järeldub omadusest 5 ja sellest, et jada, mille üldliige on aⁿ (0 < a < 1, n ∈ N), väärtused kahanevad ja lähenevad nullile.

Omaduste 1–6 põhjal saame skitseerida eksponentfunktsiooni y = a^x, 0 < a < 1 graafiku (joonis 3.3), mis on samuti pidev joon. Ka nüüd on funktsiooni graafiku asümptoodiks x-telg.

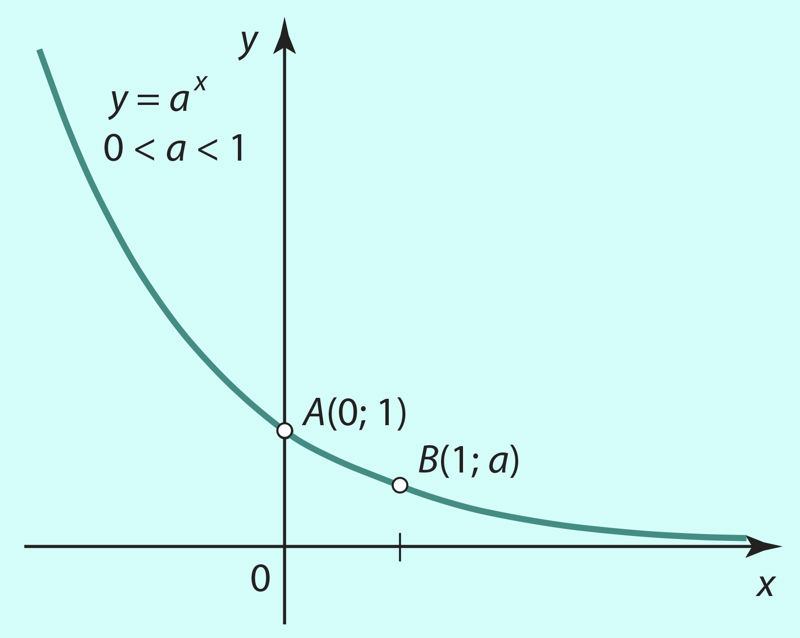Joon. 3.3

Funktsiooni y = a^x, 0 < a < 1 muutumispiirkond Y = R⁺.

Tuginedes eksponentfunktsiooni graafiku pidevusele, konstrueerime konkreetse a korral y = a^x graafiku üksikute punktide kaudu.

Näide 3. Konstrueerime funktsioonide y=2^x ja y=\left(\frac{1}{2}\right)^x graafikud.

Selleks märgime koordinaattasandile punktid, mis vastavad tabelis olevatele arvupaaridele, ning ühendame need punktid sujuva pideva joonega. Vastavad graafikud on joonistel 3.4 ja 3.5.

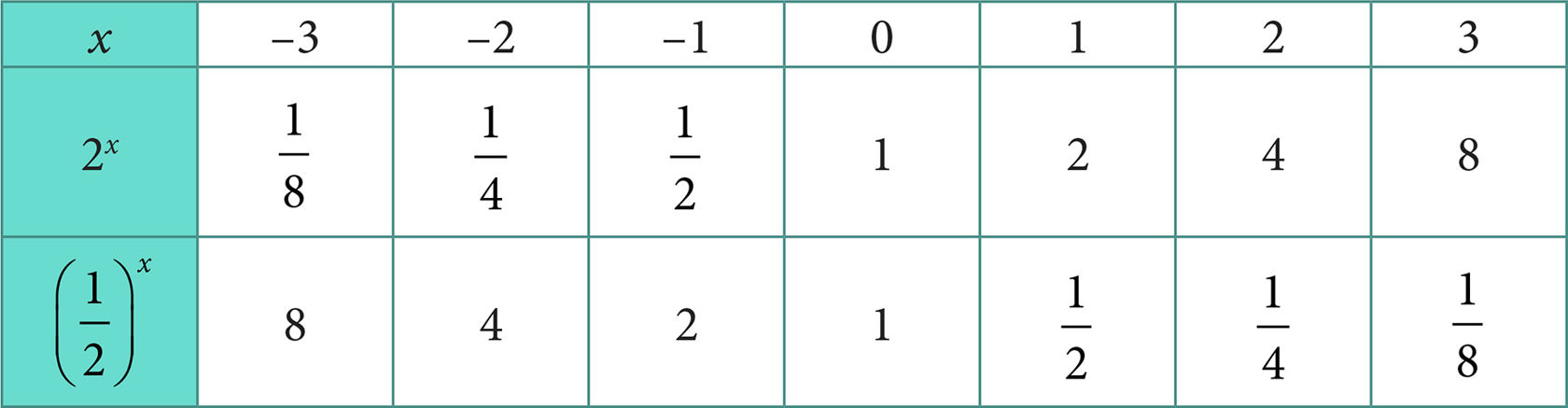
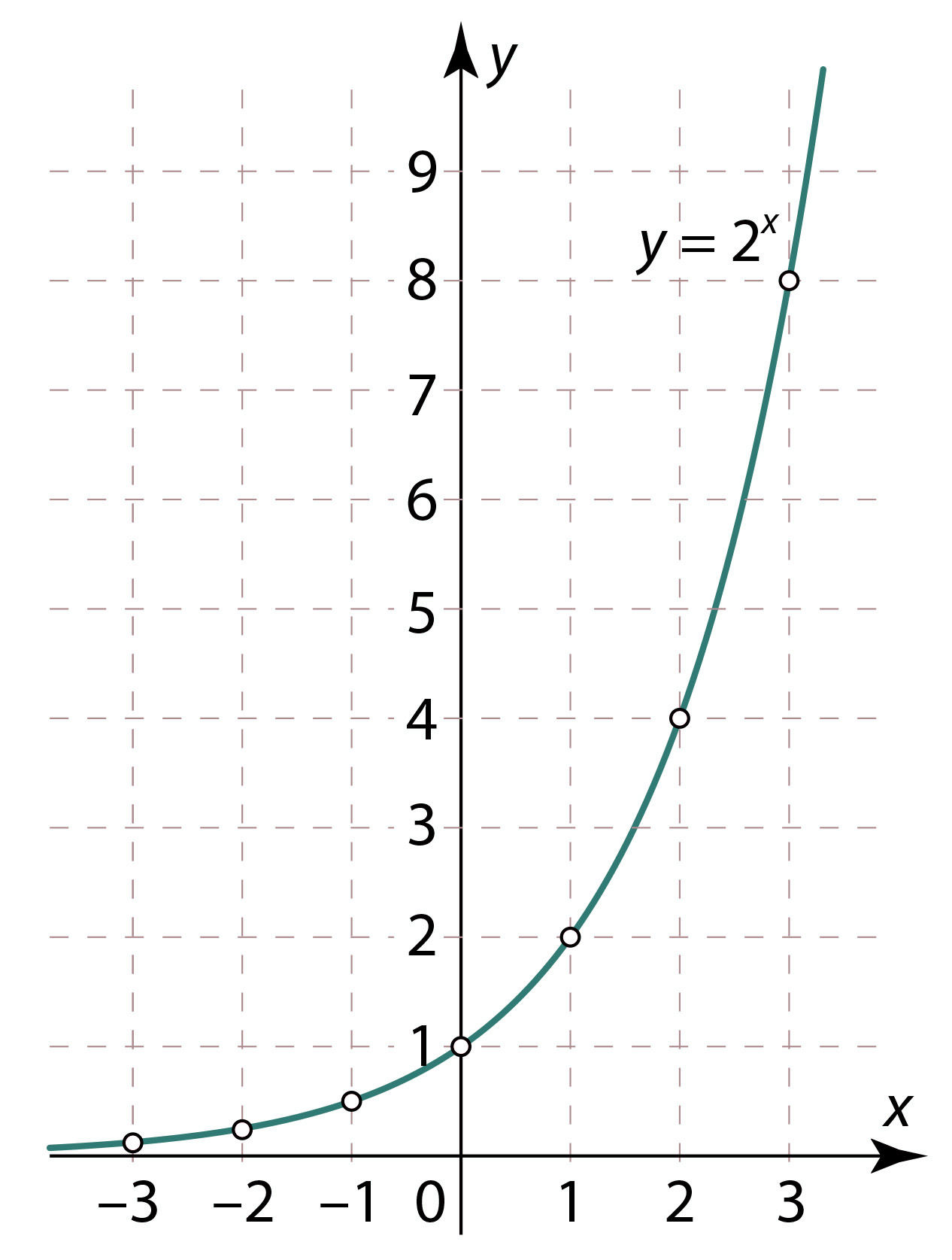Joon. 3.4

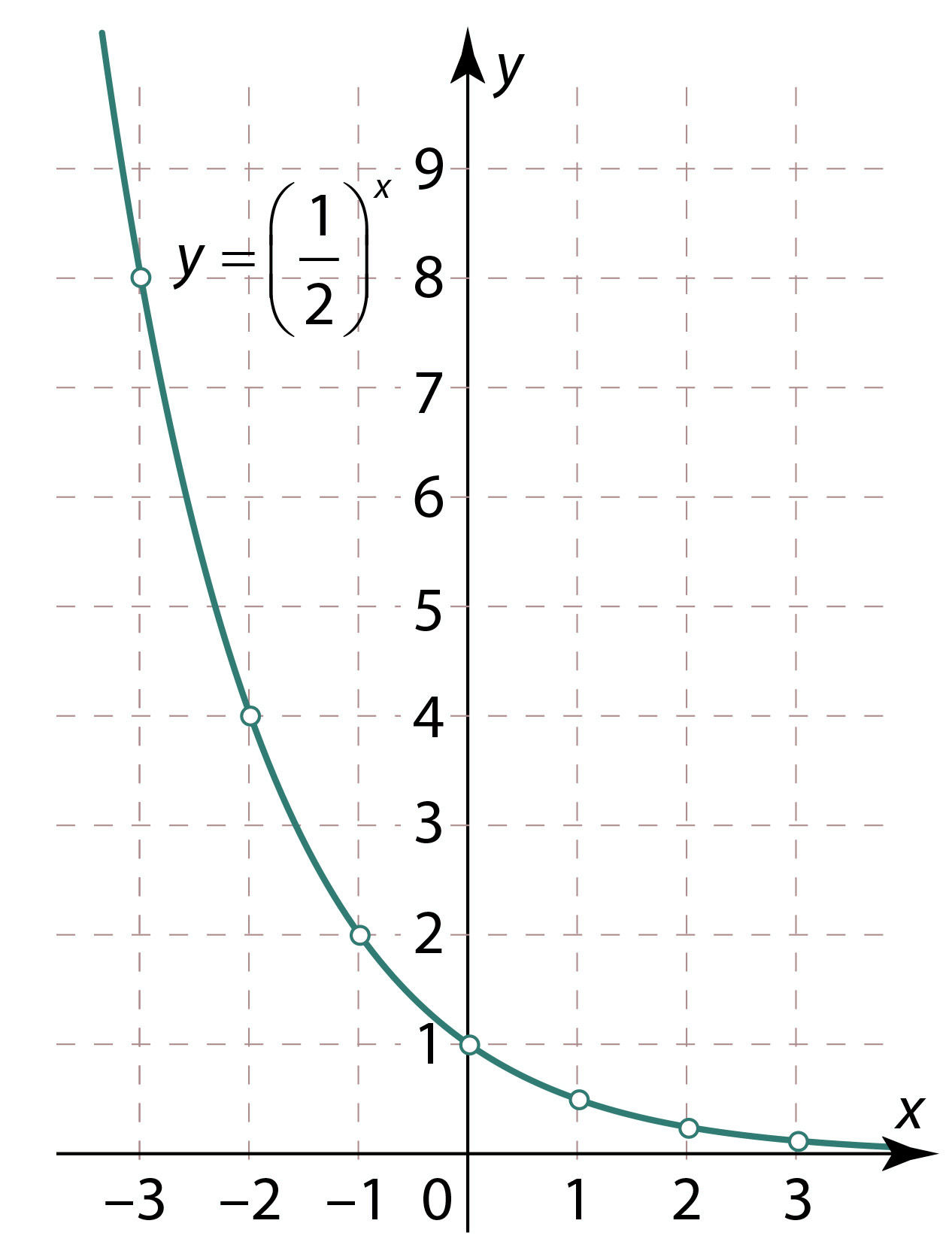Joon. 3.5

Viimasest näitest lähtudes võime väita, et

y = a^{x}

y = {(\frac{1}{a})}^{x}

graafikud on sümmeetrilised y-telje suhtes.

Väite tõestamiseks kasutame peatükis 2.14 õpitut: peegeldades funktsiooni y = f (x) graafikut y-teljest, saame funktsiooni y = f(–x) graafiku. Peegeldades nüüd funktsiooni y = a^x graafikut y-teljest, saame sellega sümmeetrilise graafiku, mis aga ongi funktsiooni y=a^{-x} ehk y=\left(\frac{1}{a}\right)^x graafik.

Kuidas muutub funktsiooni y = ax graafiku asend koordinaatteljestikus suuruse a kasvades (kahanedes), näeb joonistelt 3.6 (a > 1 korral) ja 3.7 (0 < a < 1 korral).

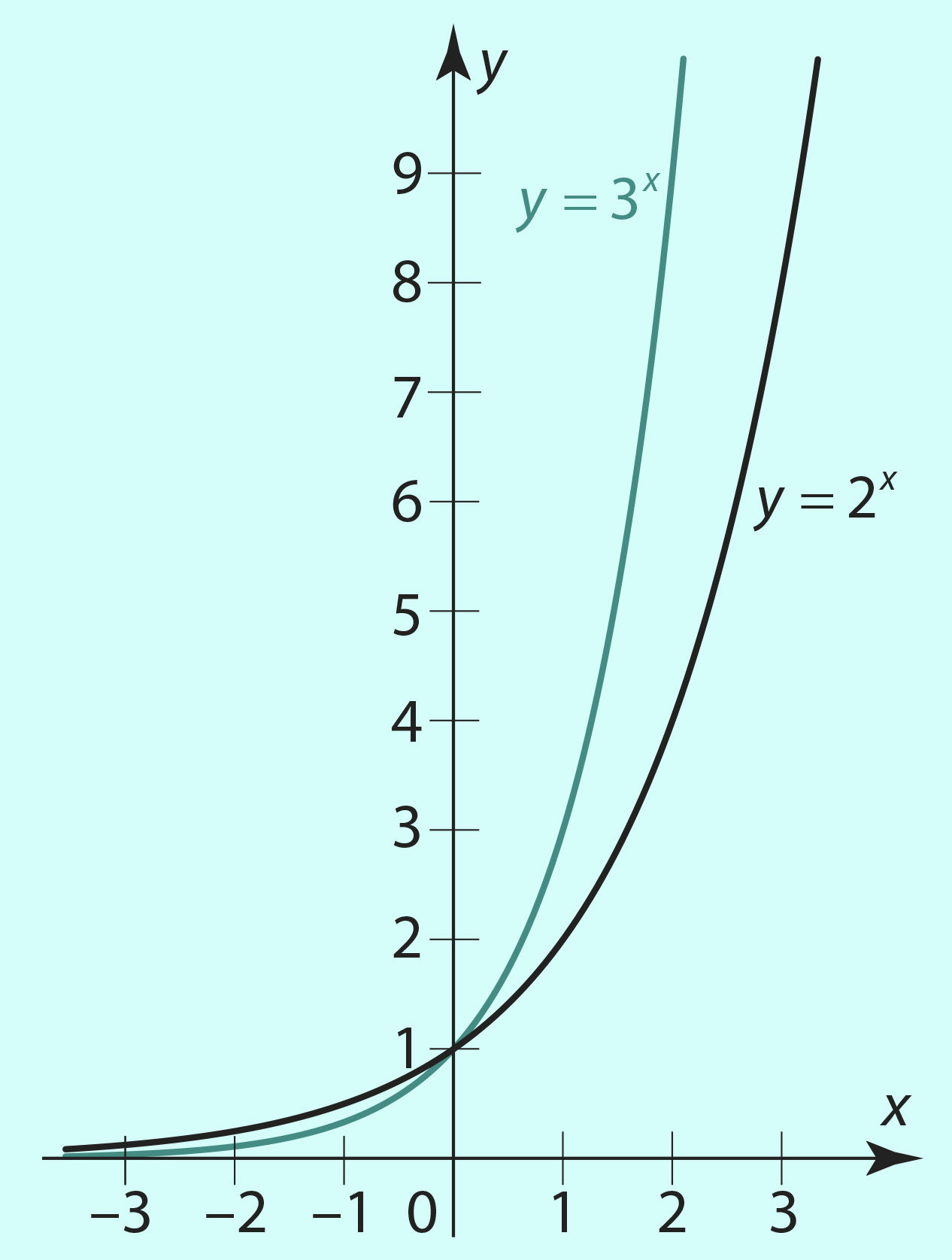Joon. 3.6

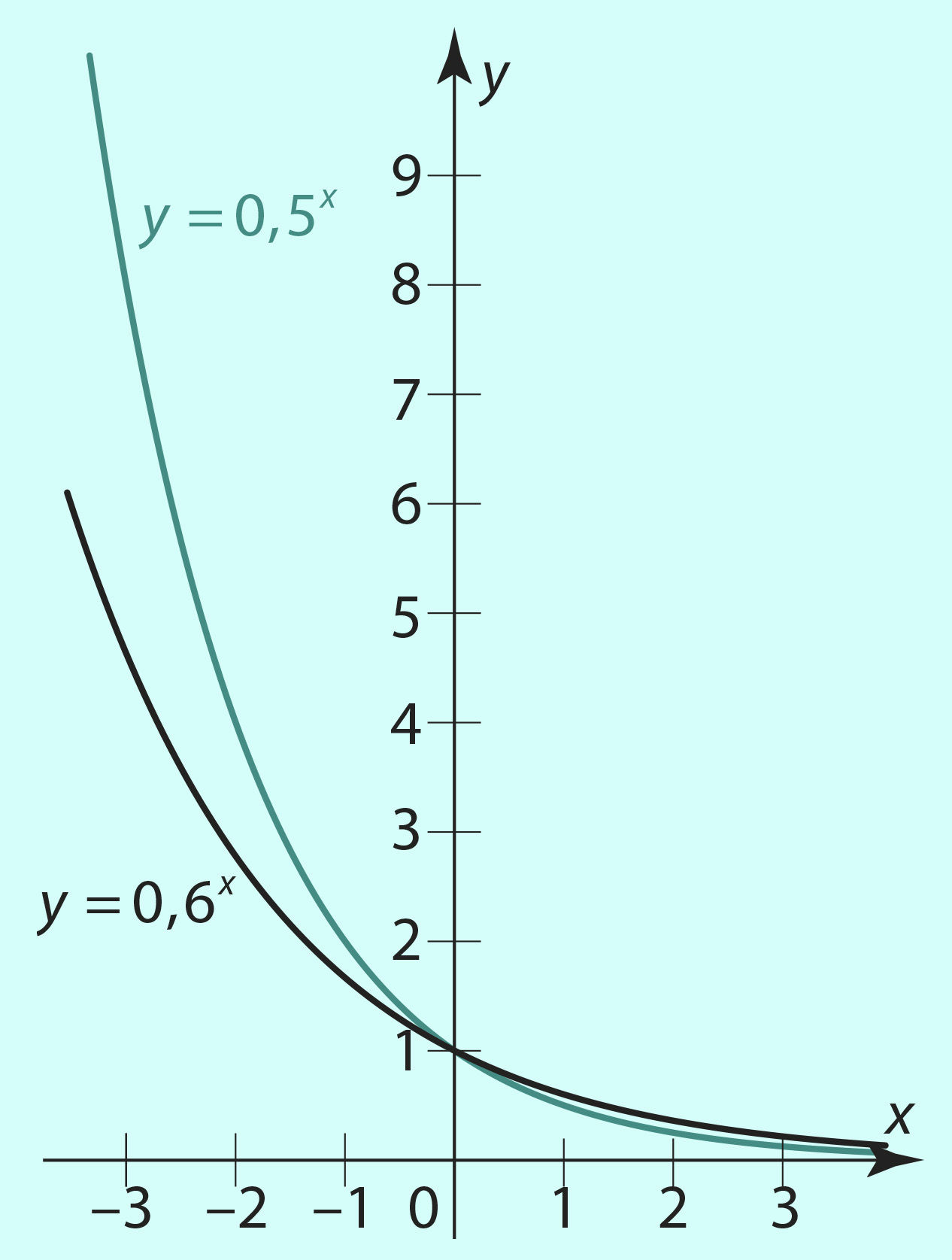Joon. 3.7

Kui mingi suurus y kasvab või kahaneb seose y = a^x järgi, siis öeldakse, et selle suuruse kasvamine (a > 1) või kahanemine (0 < a < 1) on eksponentsiaalne. Seega on ka suuruste liitprotsendiline kasvamine või kahanemine vastavalt eksponentsiaalne kasvamine või kahanemine.

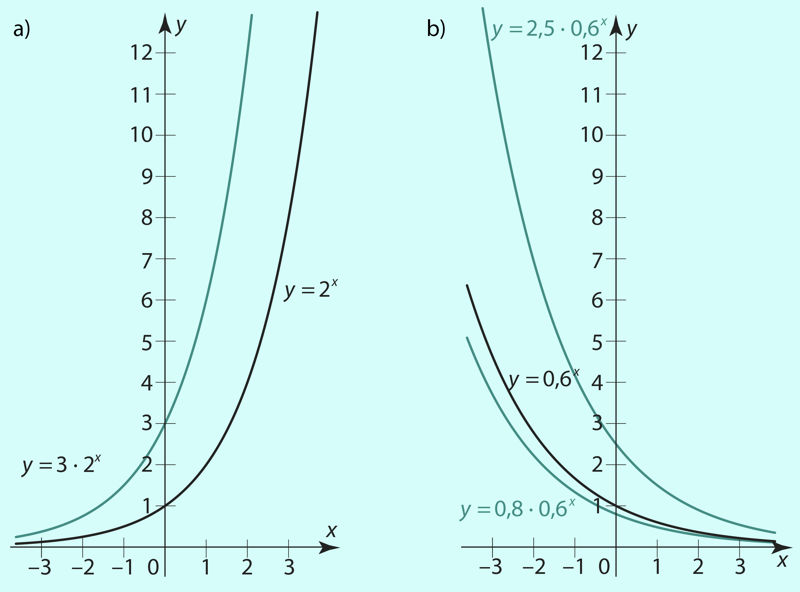
Vaatleme funktsiooni y = c · a^x. Jooniselt 3.8 a) ja b) on näha, kuidas mõjutab positiivse kordaja c muutumine graafiku asendit koordinaatteljestikus. Negatiivse kordaja –c korral on funktsiooni y = –c · a^x graafik sümmeetriline funktsiooni y = c · a^x graafikuga x-telje suhtes (joonis 3.9).

Joon. 3.8

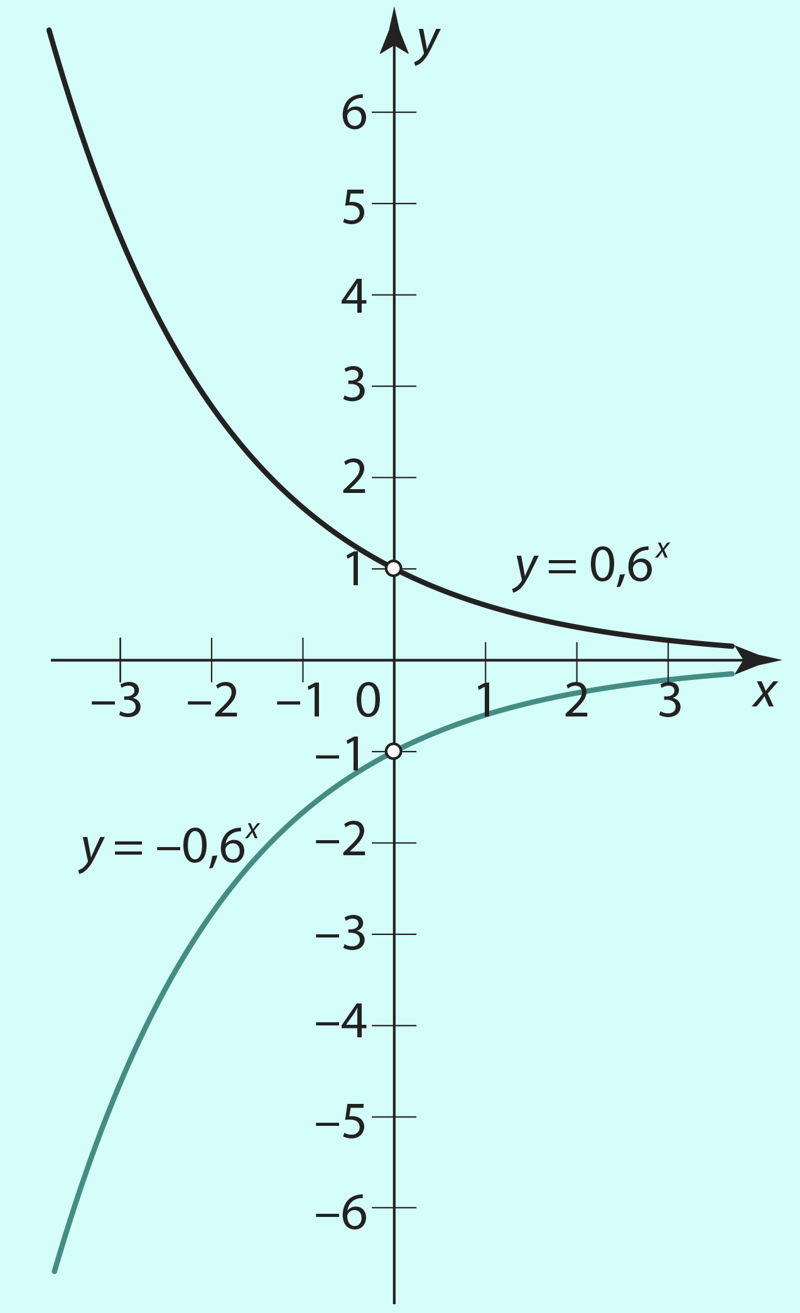Joon. 3.9

Peatüki 3.1 näites 8 lahendasime võrratused 1) 0,6^x > 0,6⁵ ja 2) 1,3^x+1 < 1,3², tuginedes teatud teoreemile reaalarvulise astendajaga astmete kohta. Selliseid võrratusi saab aga lahendada ka vastavate eksponentfunktsioonide graafikutele tuginedes.

Näide 4.

Lahendame võrratused 1) 0,6^x > 0,6⁵ ja 2) 1,3^x+1 < 1,3² vastavate eksponentfunktsioonide graafikute abil.

Funktsioon y = 0,6^x on kahanev kogu määramispiirkonnas, sest a = 0,6 < 1 (joonis 3.7). Seega vastab funktsiooni suuremale väärtusele (0,6^x) argumendi väiksem väärtus (x). Järelikult, x < 5. Võrratus ongi lahendatud.
Antud võrratuse saab kirjutada kujul 1,3 · 1,3^x < 1,3² ehk 1,3^x < 1,3¹. Et a = 1,3 > 1, siis on funktsioon y = 1,3^x kasvav. See tähendab, et funktsiooni suurem väärtus vastab argumendi suuremale väärtusele. Järelikult x < 1.

Eksponentfunktsioonide graafikute võrdlemise teel saab lahendada ka keerukamaid võrratusi.

Näide 5.

Lahendame võrratused 1) 2^x > 3^x ja 2) 2^x>\left(\frac{1}{2}\right)^x.

Vaatleme võrratuste erinevaid lahendusviise.

Jooniselt 3.6 nähtub, et vaid x < 0 korral on funktsiooni y = 2^x väärtused suuremad funktsiooni y = 3^x väärtustest (y = 2^x graafik asub kõrgemal kui y = 3^x graafik). Seega on esimese võrratuse lahendiks x < 0.
Jooniseid 3.4 ja 3.5 võrreldes näeme, et vaid piirkonnas x > 0 on funktsiooni y = 2^x graafik kõrgemal kui funktsiooni y=\left(\frac{1}{2}\right)^x graafik. Järelikult on võrratuse lahendiks x > 0.

Neid võrratusi saab lahendada ka näite 4 eeskujul.

Selleks jagame esimese võrratuse positiivse suurusega 3^x. Tulemusena saame võrratuse \left(\frac{2}{3}\right)^x>1 ehk \left(\frac{2}{3}\right)^x>\left(\frac{2}{3}\right)^0. Viimasest võrratusest järeldubki näite 4 eeskujul, et x < 0. Võrratuse \left(\frac{2}{3}\right)^x>1 oleksime võinud lahendada aga ka funktsiooni y=\left(\frac{2}{3}\right)^x graafiku abil, leides argumendi x väärtuste piirkonna, mille korral funktsiooni väärtused on suuremad kui 1.
Jagame võrratuse 2^x>\left(\frac{1}{2}\right)^x positiivse suurusega \left(\frac{1}{2}\right)^x. Tulemusena saame võrratuse 4^x > 1 ehk 4^x > 4⁰. Nüüd järeldubki näite 4 eeskujul, et x > 0. Võrratuse 4^x > 1 lahendamist võib vaadelda ka piirkonna leidmisena, kus funktsiooni y = 4^x väärtused on suuremad kui 1.

Seotud sisu

Ülesanded A

Ülesanne 589. Eksponentfunktsiooni graafik

Konstrueerige ühes ja samas koordinaatteljestikus funktsioonide y=\left(\frac{3}{4}\right)^x, y=\left(\frac{1}{5}\right)^x ja y=\left(\frac{1}{10}\right)^x graafikud. Kuidas mõjutab a muutumine (a < 1) graafiku asendit teljestikus?

Milline on nende funktsioonide määramispiirkond, positiivsuspiirkond, negatiivsuspiirkond, kasvamisvahemik, kahanemisvahemik, ekstreemumkohad?

	y=\left(\frac{3}{4}\right)^x	y=\left(\frac{1}{5}\right)^x	y=\left(\frac{1}{10}\right)^x
X
X^+
X^-
X\uparrow
X\downarrow
X_e

Ülesanne 590. Eksponentfunktsiooni graafik

Ülesanne 591. Eksponentfunktsiooni graafik

Konstrueerige ühes ja samas koordinaatteljestikus funktsioonide y=\left(\frac{1}{3}\right)^x ja y=3^x graafikud. Kuidas paiknevad need graafikud teineteise suhtes?

Ülesanne 592. Terastross

Joon. 3.10

Vastus. Kui silindril on 0,5 keerdu, siis tasakaalustada saab jõudu N; kui silindril on 1 keerd, siis N; kui silindril on 1,25 keerdu, siis N; kui silindril on 2 keerdu, siis N; kui silindril on 3 keerdu, siis N.

Joon. 2.44

Vastus. Kui silindril on 1 keerd, siis tasakaalustamiseks läheb vaja jõudu N; kui silindril on 1,5 keerdu, siis N; kui silindril on 2 keerdu, siis N; kui silindril on 3 keerdu, siis N; kui silindril on 4 keerdu, siis N; kui silindril on 5 keerdu, siis N.

Ülesanne 593. Pärmi kasvamine

Vastus. 2 tunni möödudes on kg pärmi; 3,5 tunni möödudes kg; 6 tunni möödudes kg; 8 tunni möödudes kg; 9 tunni möödudes kg.

Konstrueerige pärmi kasvamist kirjeldava funktsiooni p = 90 · 1,2^t graafik ajavahemikus 0 kuni 9 tundi.

Ülesanne 594. Kohvi jahtumine

5 minuti pärast?
Vastus. 5 minuti pärast on kohvi temperatuur °.
15 minuti pärast?
Vastus. 15 minuti pärast on kohvi temperatuur °.

Mitme minuti pärast on kohvi temperatuur 15°?

Milline sirge on selle funktsiooni graafiku asümptoodiks?

Vastus. Sirge y = .

Seotud sisu

Ülesanded B

Ülesanne 595. Eksponentfunktsiooni graafik

	X	X^+	X^-	X\uparrow	X\downarrow	X_e
y=1,5^x
y=1,5^x+2
y=1,5^x-3

Ülesanne 596. Eksponentfunktsiooni graafik

Ülesanne 597. Eksponentfunktsiooni graafik

Funktsiooni y = c f (x), c > 0, väärtused on c korda suuremad kui vastavad y = f (x) väärtused. Seega tuleb y = c f (x) graafiku punktid märkida x-teljest c korda kaugemale kui y = f (x) punktid.

Joonestage koordinaatteljestikku y = 1,4^x graafik ning y = 3 · 1,4^x ja y=\frac{1}{2}\cdot1,4^x graafik.

Ülesanne 598. Eksponentfunktsiooni graafik

Vastus. X = , X^+ = , X^- = , X\uparrow = , X\downarrow = , X_e =

Ülesanne 599. Ekponentvõrratuse lahendamine

3^x>3^6
x

10^x>100
x

0,8^x>0,8^5
x

2^{2x}<64
x

0,5^x<0,5^3
x

10^{x+1}<100
x

0,1^3<0,1^x
x

4^x>16
x

11^{x+1}>121
x

8\cdot3^{2x-3}<4^3
x

0,36\cdot0,6^x<0,36^{x-1}
x

100\cdot10^5>100^{x-2,5}
x

0,008>0,2^{x-5}
x

3\cdot2^x>2^x
x

0,7\cdot4^x>4^x
x

3^x>2^x
x

5^x<3^x
x

\left(\frac{1}{2}\right)^x<2^x
x

Ülesanne 600. Eksponentfunktsioon

Vastus. a₁ = , q = , a_n =

Leidke funktsiooniga y = 0,2 · 2^x, kus x ∈ {0; 1; 2; …} määratud geomeetrilise jada kümnes liige ja kümne esimese liikme summa.

Vastus. a₁₀ = , S₁₀ =

Ülesanne 601. Eksponentfunktsioon

negatiivsed? Millal?
Vastus. Jada liikmed olla negatiivsed, kui .
vahelduvate märkidega? Millal?
Vastus. Jada liikmed olla vahelduvate märkidega, kui .

Milline on geomeetrilise jada esimene liige, tegur ja üldliige siis, kui funktsiooni y = c · a^x määramispiirkond on {1; 2; 3; …}?

Vastus. a₁ = , q = , a_n =

Ülesanne 602. Eksponentfunktsioon

tõkestamatult kasvav?
Vastus. Kui c , a .
hääbuv?
Vastus. Kui c , a .

Ülesanne 603. Eksponentfunktsioon

Funktsioon	Jada 4 esimest liiget	a₁	q
y=4^x	; ; ; ; ...
y=2\cdot3^x	; ; ; ; ...
y=-3\cdot2^x	; ; ; ; ...
y=\left(\frac{1}{10}\right)^x	; ; ; ; ...

Ülesanne 604. Eksponentfunktsioon

y=4^x
y=2\cdot3^x

y=-3\cdot2^x
y=\left(\frac{1}{10}\right)^x

Ülesanne 605. Eksponentfunktsioon

Et a₁ = 2 ja q = 7, siis y = 2 · 7^x, kus x ∈ {0; 1; 2; …} või y=\frac{2}{7}\cdot7^x, kus x ∈ {1; 2; 3; …}.

Et eksponentfunktsiooni korral a > 0, siis vahelduvate märkidega geomeetrilisele jadale (näiteks –5; 10; –20; …) eksponentfunktsiooni ei vasta.

Leidke antud geomeetrilisele jadale vastav eksponentfunktsioon, kui see on olemas:

1; 5; 25; …;
–64; –32; –16; …;

14; 10; 7\frac{1}{7}; …;
3; –6; 12; …;

Ülesanne 606. Eksponentfunktsioon

6; 6; 6; …
101; 202; 303; ...
1; 2; 3; …
10; 100; 1000; …

Geomeetriliste jadade korral leidke vastav eksponentfunktsioon, kui see on olemas.

Seotud sisu

Opiqus edenemine

	Tööd
	Peatükk on läbi töötatud

Eksponent­funktsioon

Seotud sisu

Ülesanded A

Ülesanne 589. Eksponent­funktsiooni graafik

Ülesanne 590. Eksponent­funktsiooni graafik

Ülesanne 591. Eksponent­funktsiooni graafik

Ülesanne 592. Teras­tross

Ülesanne 593. Pärmi kasvamine

Ülesanne 594. Kohvi jahtumine

Seotud sisu

Ülesanded B

Ülesanne 595. Eksponent­funktsiooni graafik

Ülesanne 596. Eksponent­funktsiooni graafik

Ülesanne 597. Eksponent­funktsiooni graafik

Ülesanne 598. Eksponent­funktsiooni graafik

Ülesanne 599. Ekponent­võrratuse lahendamine

Ülesanne 600. Eksponent­funktsioon

Ülesanne 601. Eksponent­funktsioon

Ülesanne 602. Eksponent­funktsioon

Ülesanne 603. Eksponent­funktsioon

Ülesanne 604. Eksponent­funktsioon

Ülesanne 605. Eksponent­funktsioon

Ülesanne 606. Eksponent­funktsioon

Seotud sisu

Lisa materjali

Lisatavad failid

Teata veast

Teata siia ainult Opiqu veast. Palun kirjelda viga nii täpselt kui võimalik.

Kui ootad Opiqu meeskonnalt vastust, lisa oma kontaktandmed (e-post, telefon).

Tee linnuke, et aidata meil spämmiga võidelda

Opiq kasutab küpsiseid

Eksponentfunktsioon

Ülesanne 589. Eksponentfunktsiooni graafik

Ülesanne 590. Eksponentfunktsiooni graafik

Ülesanne 591. Eksponentfunktsiooni graafik

Ülesanne 592. Terastross

Ülesanne 595. Eksponentfunktsiooni graafik

Ülesanne 596. Eksponentfunktsiooni graafik

Ülesanne 597. Eksponentfunktsiooni graafik

Ülesanne 598. Eksponentfunktsiooni graafik

Ülesanne 599. Ekponentvõrratuse lahendamine

Ülesanne 600. Eksponentfunktsioon

Ülesanne 601. Eksponentfunktsioon

Ülesanne 602. Eksponentfunktsioon

Ülesanne 603. Eksponentfunktsioon

Ülesanne 604. Eksponentfunktsioon

Ülesanne 605. Eksponentfunktsioon

Ülesanne 606. Eksponentfunktsioon