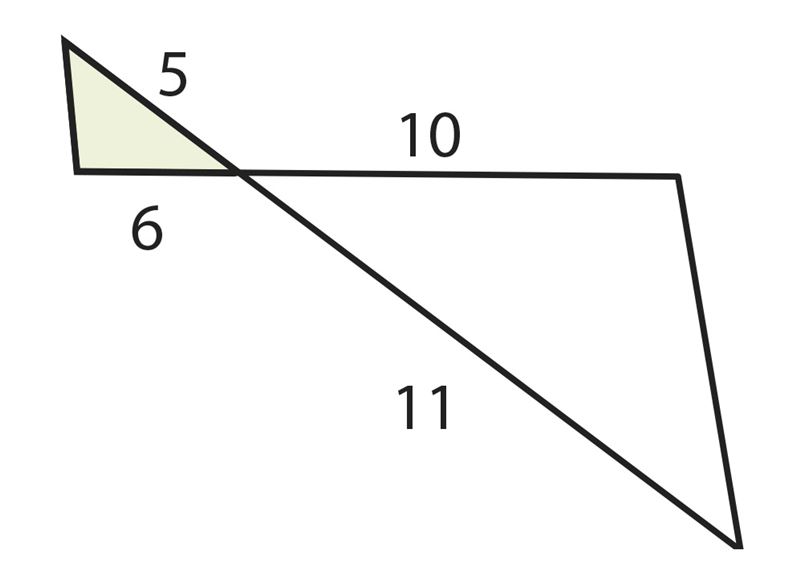
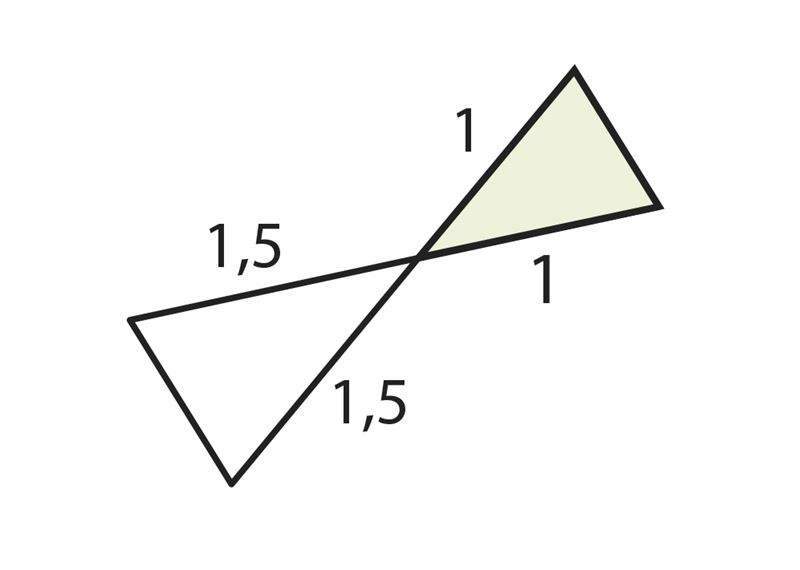
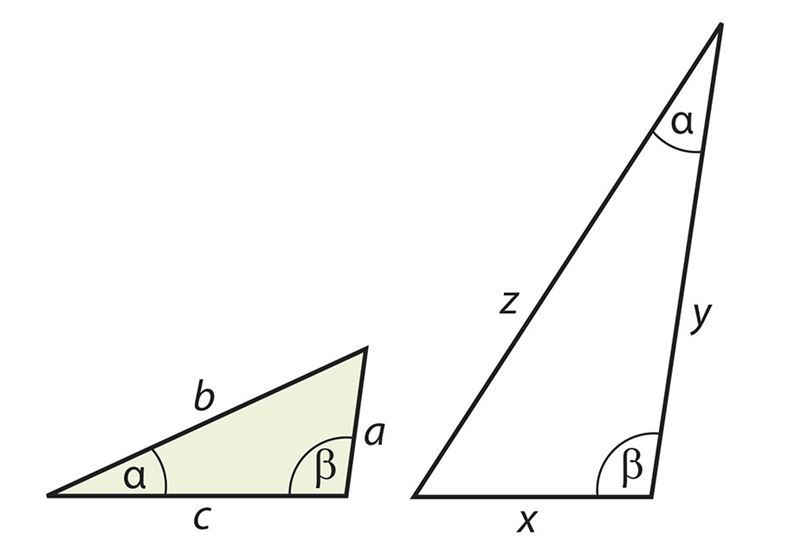
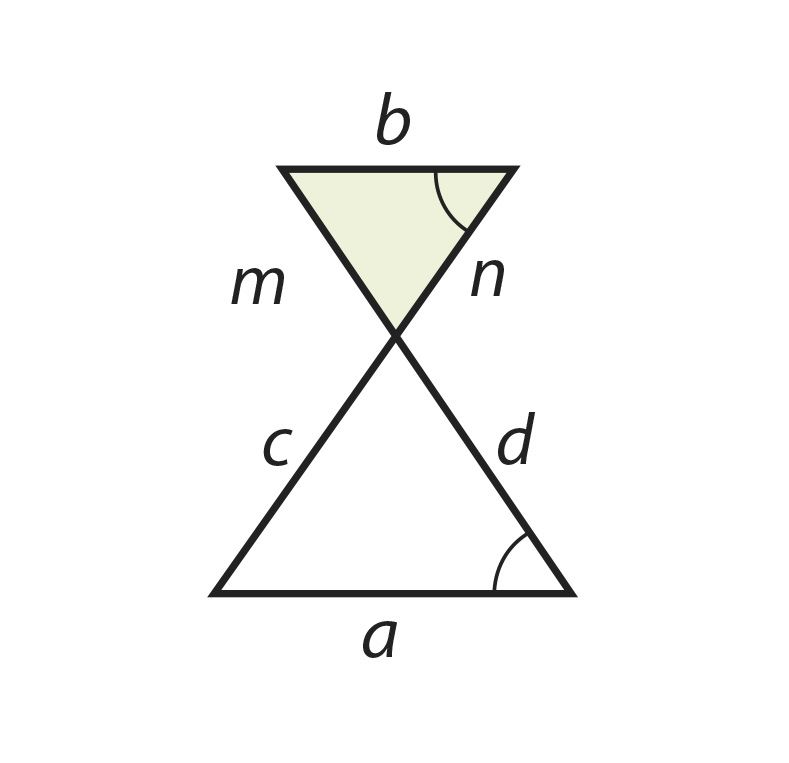В предыдущем параграфе мы определили подобные треугольники, как треугольники с пропорциональными сторонами. Теперь рассмотрим два признака, позволяющие установить подобие треугольников.

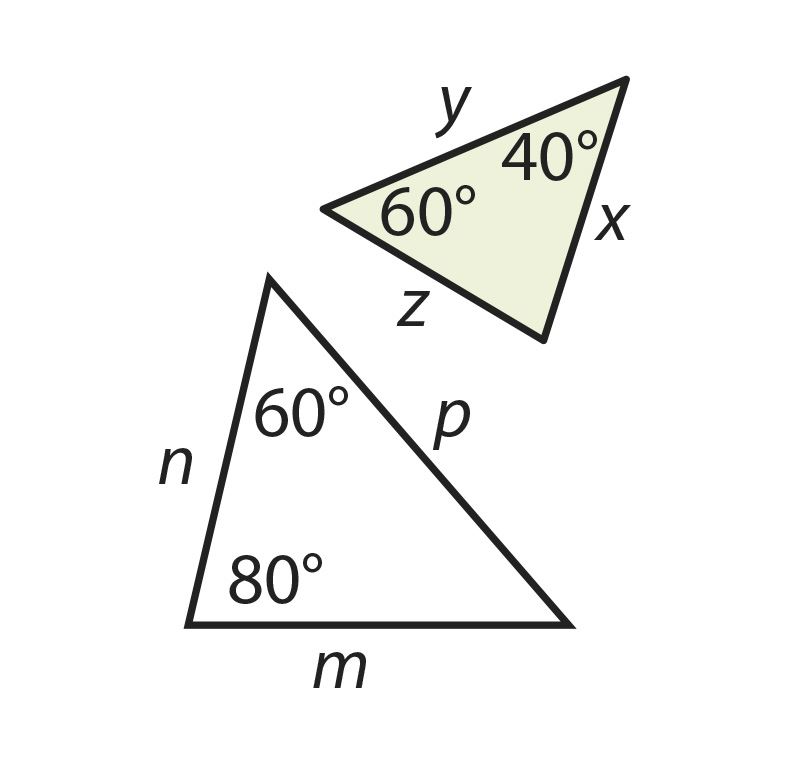
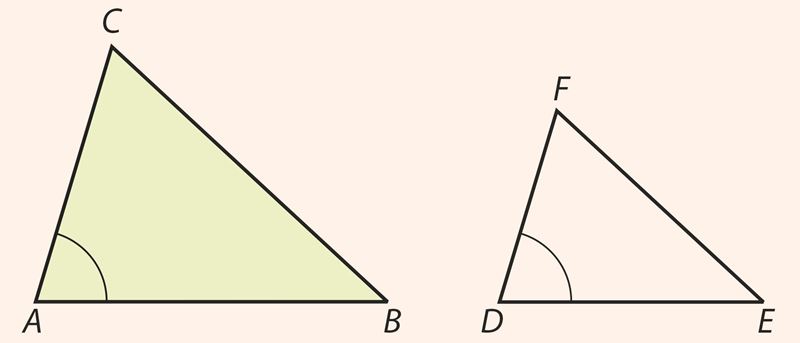
1. Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
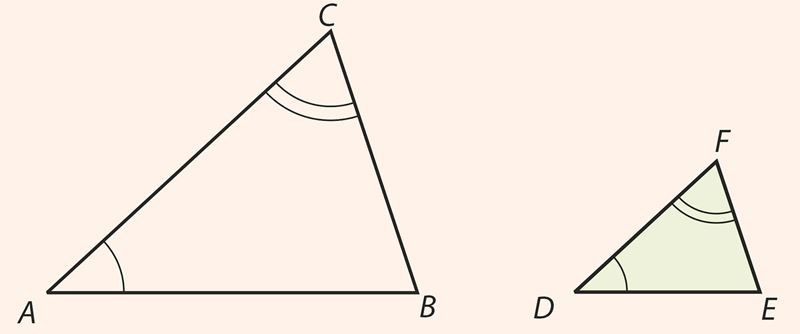
Этот признак называется признаком подобия по двум углам. Докажем эту теорему.
Условие. ∠A = ∠D, ∠C = ∠F.
Заключение. ∆ABC ∼ ∆DEF.
Доказательство. Для доказательства отметим на сторонах АВ и ВС треугольника АВС соответственно точки M и N так, что AN = DF и ∠ANM = ∠ACB.
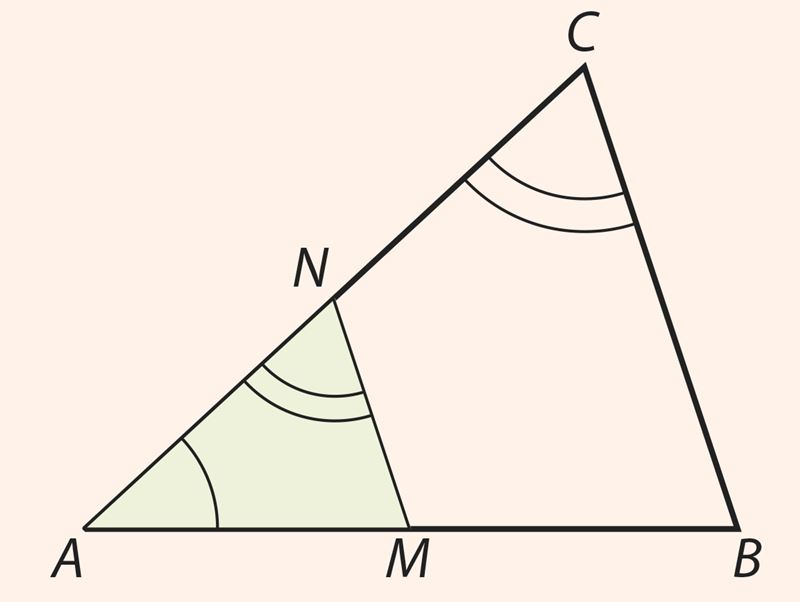 | ||||||||
Запишем следующие последовательные заключения:
- ∆AMN = ∆DEF – признак равенства треугольников УСУ;
- MN || BC, так как ∠ANM = ∠ACB;
- ∆ABC ∼ ∆AMN – следует из пункта 2 и § 5.4;
- ∆ABC ∼ ∆DEF – следует из пунктов 3 и 1. ■
 |
||||||||
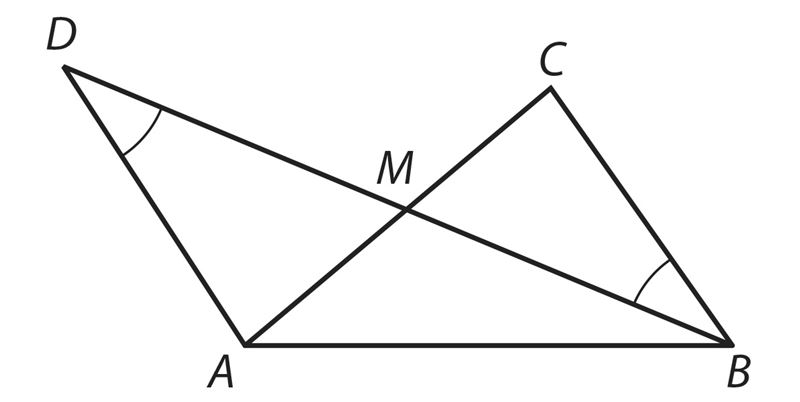
С помощью доказанного признака мы можем убедиться, что для изображенных на рисунке треугольников ∆KLM ∼ ∆PLQ, так как ∠MKL = ∠LPQ (по рисунку) и ∠KLM = ∠PLQ (вертикальные углы).
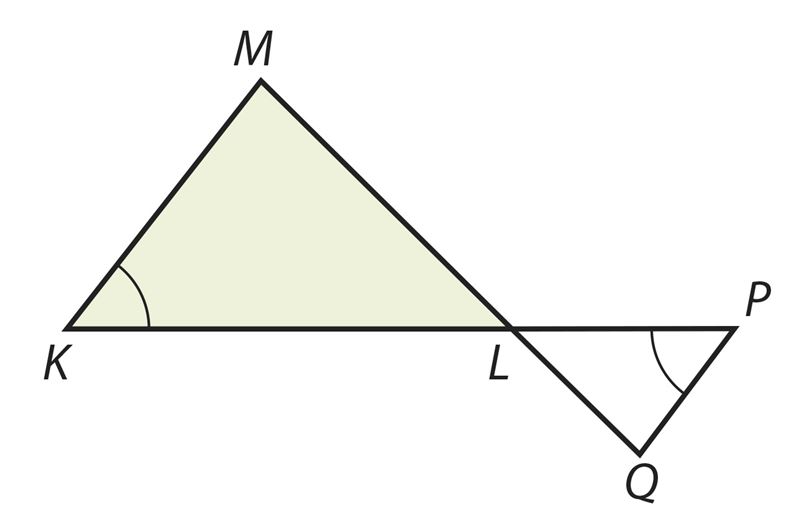
Поэтому можем записать
.
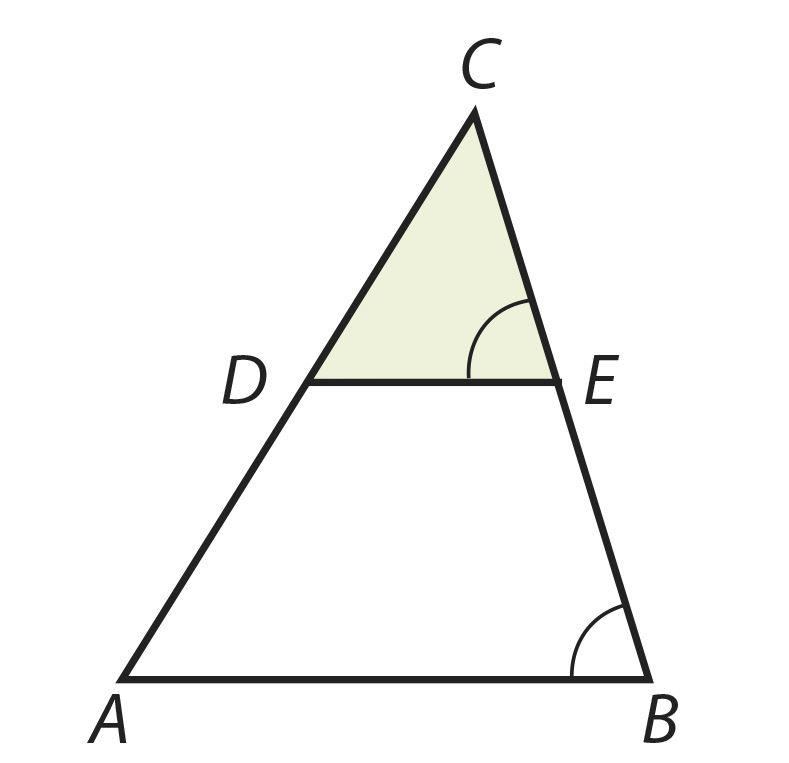
Второй признак подобия треугольников мы представим без доказательства. Постарайся хорошо усвоить его содержание.

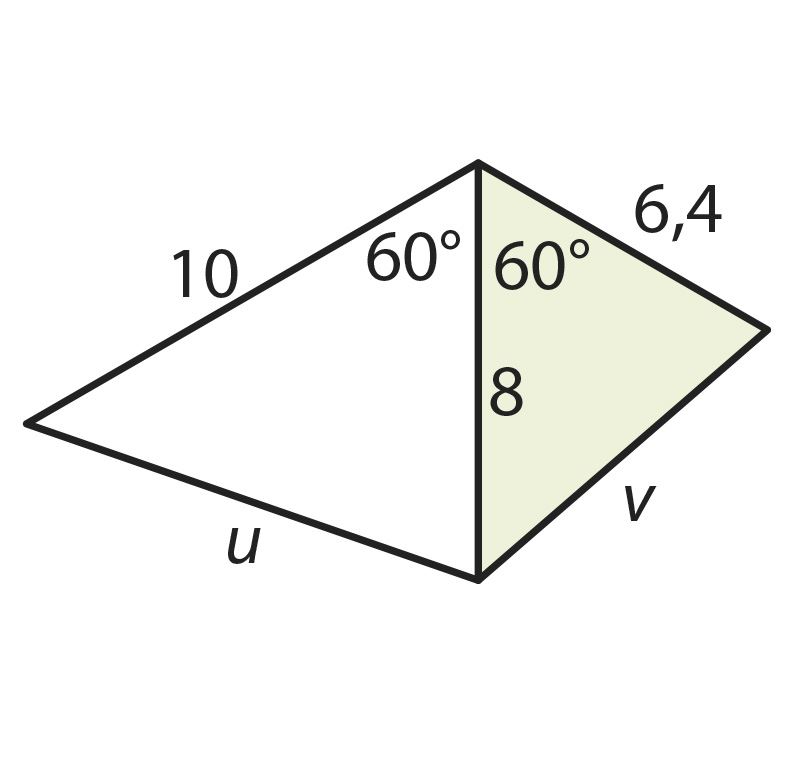
2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Этот признак называется признаком подобия треугольников по двум сторонам и углу между ними.
 |
||||||||
Согласно этому признаку мы можем утверждать, что ∆ABC ∼ ∆KLM, так как ∠B = ∠M и .
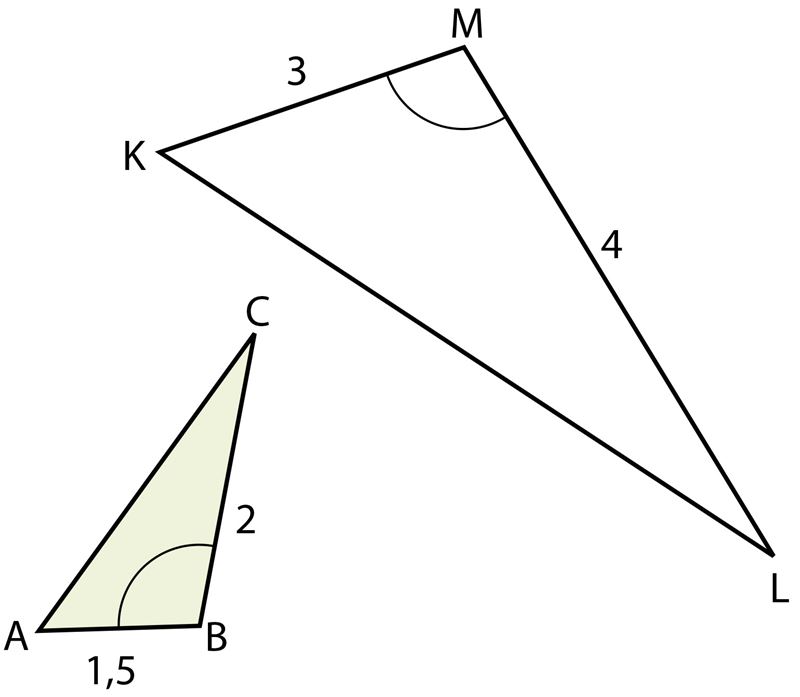
Из подобия треугольников можно, в свою очередь, вывести, что и ∠A = ∠K, ∠C = ∠L.

Теперь мы имеем в итоге три признака, каждый из которых позволяет установить, подобны данные треугольники или нет:
- теорема 1 – признак подобия треугольников по двум углам (УУ);
- теорема 2 – признак подобия треугольников по двум сторонам и углу между ними (СУС);
- определение подобия треугольников (§ 5.4), в котором выражается подобие треугольников по трем сторонам (ССС).
Упражнения A
 |
||||||||
Треугольник Т1 | Треугольник Т2 | Подобны ли? |
50° и 60° | 70° и 60° | |
100° и 20° | 50° и 100° | |
75° и 45° | 75° и 60° | |
38° и 52° | 52° и 90° | |
111° и 59° | 59° и 10° |
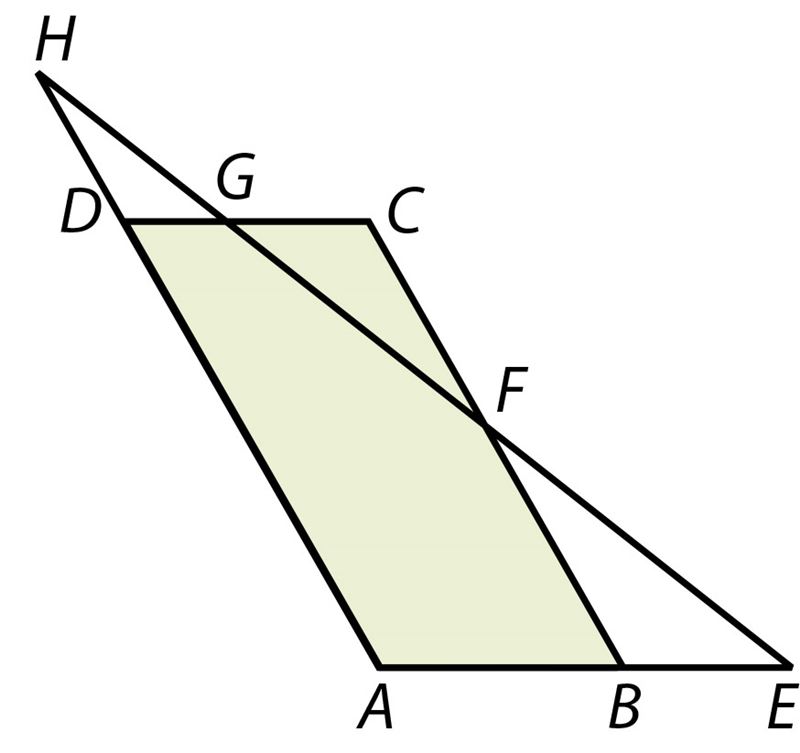 | ||||||
Ответ: BC = см, BE = см.
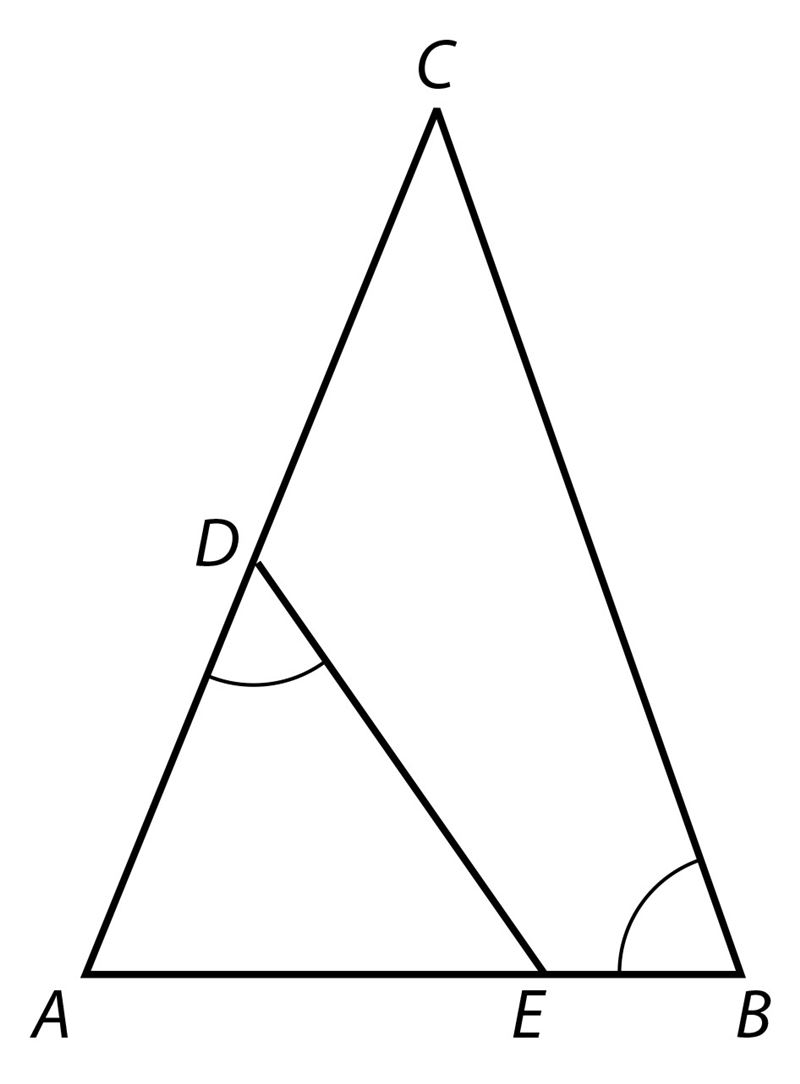
 | ||||||
x =
Ниже даны величины острого угла α одного прямоугольного треугольника и острого угла β другого прямоугольного треугольника. Определи, подобны ли эти треугольники (устно). Отметь случаи подобных треугольников.
- α = 40°, β = 50°
- α = 75°, β = 15°
- α = 35°, β = 65°
- α = 42°, β = 47°
- α = 12°, β = 78°
- α = 11°, β = 89°
Ответ: второй катет равен см.
- α = 80°, β = 50°
- α = 40°, β = 70°
- α = 62°, β = 58°
- α = 91°, β = 45°
- α = 12°, β = 84°
- α = 60°, β = 60°
Ответ: боковая сторона этой трапеции равна см.
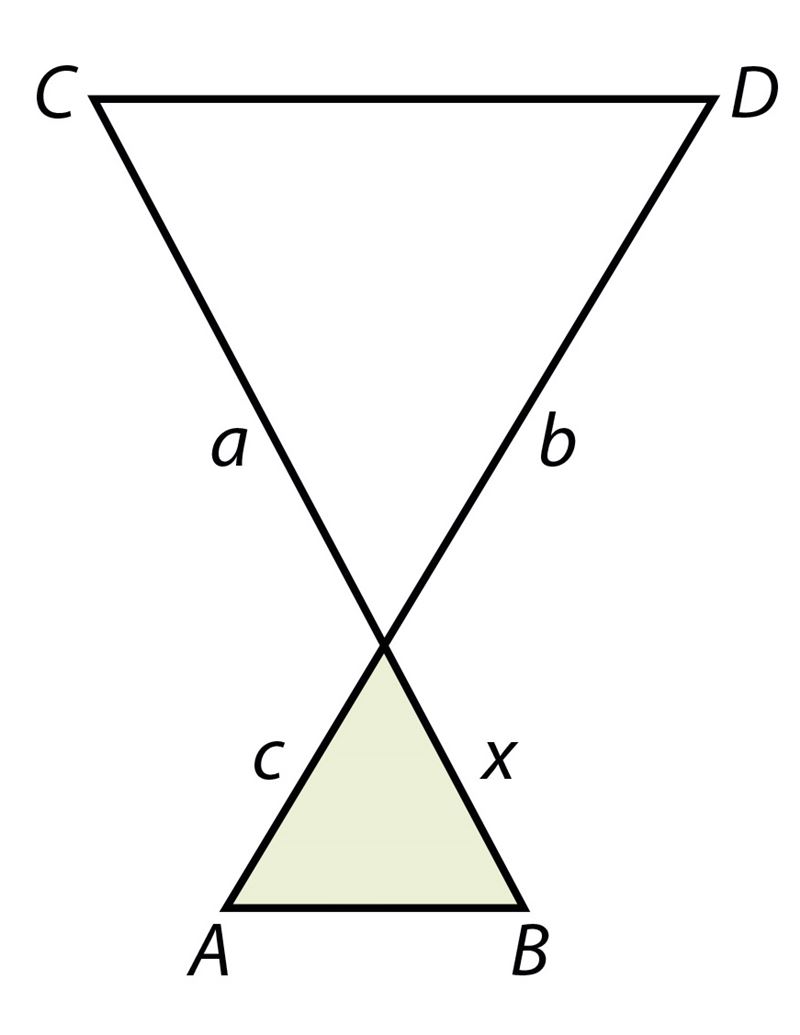
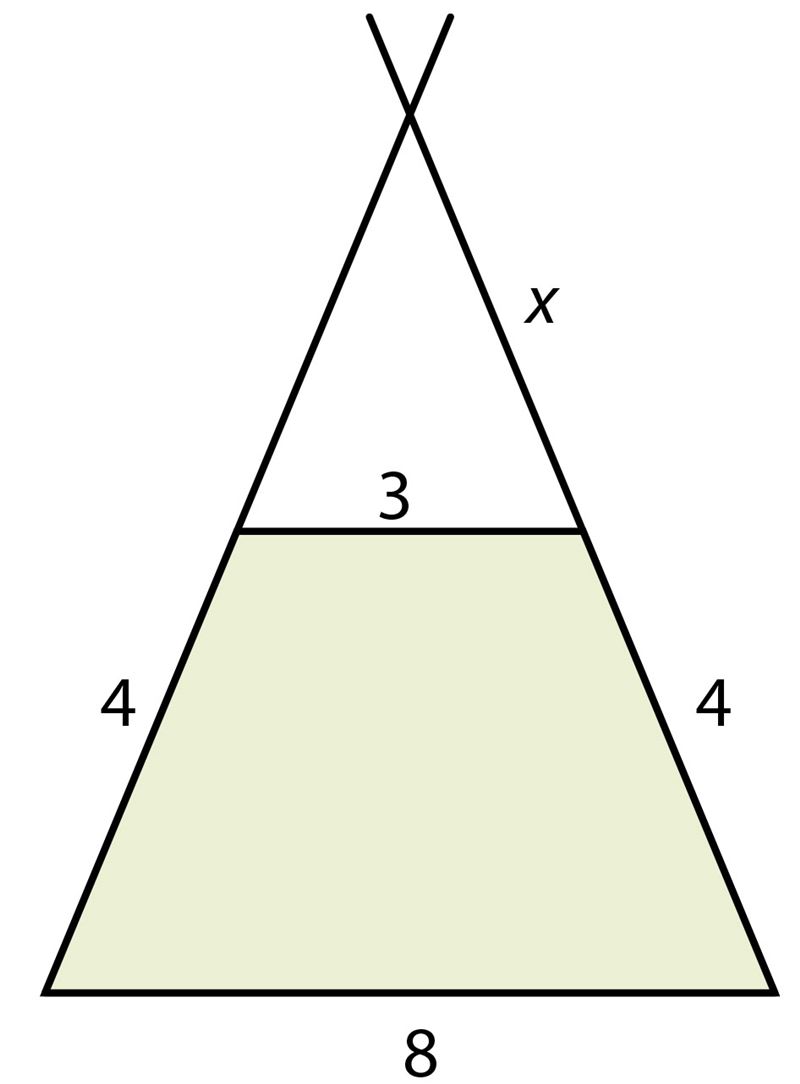 | ||||||
Ответ: боковые стороны нужно удлинить на дм.
Ответ: боковая сторона трапеции равна см.
Ответ: боковая сторона равна см.
Ответ: BC = см и CD = см.
Ответ: эти треугольники подобными.
Ответ: эти треугольники подобными.
Ответ: данное утверждение .
856. Признаки подобия треугольников
Начерти прямоугольный треугольник АВС и его высоту CD, проведенную из вершины прямого угла к гипотенузе. Найди на чертеже пары подобных треугольников. Запиши равные углы и отношения соответственных сторон.
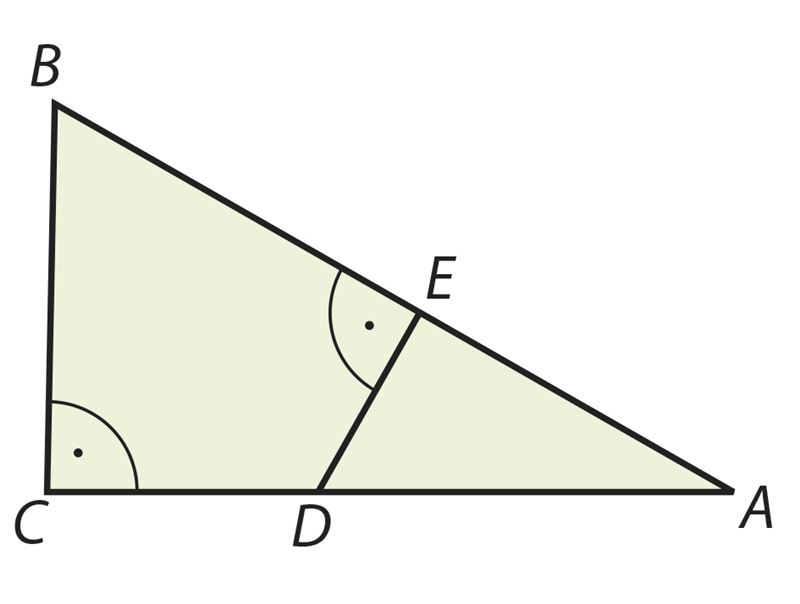
Ответ: BE =
Упражнения Б
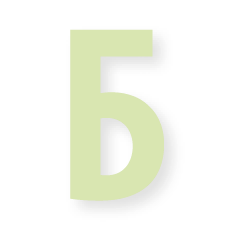 |
||||||||
858. GeoGebra
С помощью программы GeoGebra начерти два треугольника так, что два угла одного треугольника соответственно равны двум углам другого треугольника. Убедись, что эти треугольники подобны. Для этого найди отношения соответственных сторон.
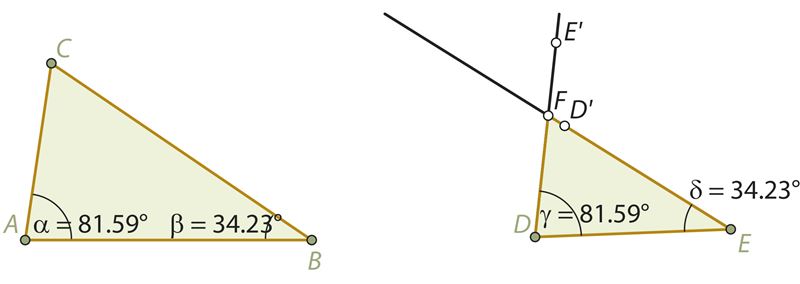
Указание. Первый треугольник начерти произвольно. С помощью инструмента «Угол» найди два угла этого треугольника. Построение второго треугольника начни с некоторого отрезка DE. От концов этого отрезка отложи углы первого треугольника с помощью инструмента «Угол заданной величины» Проведи вторые стороны этих углов (лучи DE´ и ED´) и найди точку их пересечения F, которая будет третьей вершиной второго треугольника.
Треугольники с соответственно равными углами можно построить также с помощью признаков параллельности прямых.
Ответ: EF = см, DF = см, AC = см.
Ответ: BC = см, EF = см.
Ответ: AB = см, DE = см.
- CF · AK = AE · KC
- CF · KE = AE · KF
Ответ: периметр треугольника ABC равен см.
Ответ: AC = см, DF = см.
Ответ: периметр треугольника BDE равен мм.
Ответ: AF =
Ответ: LQ =
Ответ: BE = см и тогда SADE = см2 или BE = см и тогда SADE = см2.
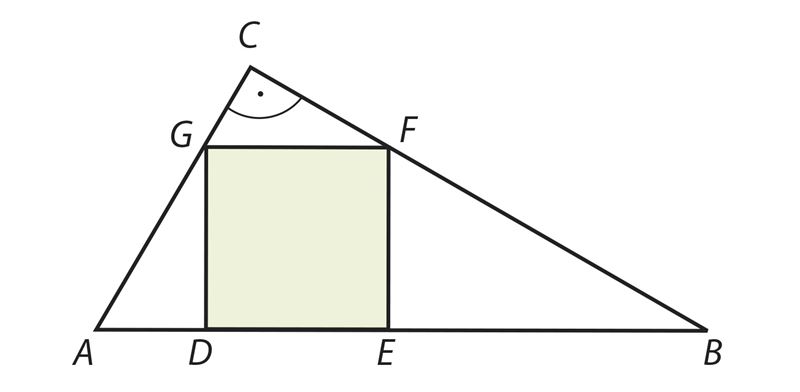
- ∆ADG ∼ ∆GCF
- ∆ADG ∼ ∆FEB
- AD · EB = DG · FE
- DE2 = AD · EB
Ответ: SADO = см2, SABO = см2, SBCO = см2, SCDO = см2.