Kang
Aia taga oli suur kivi. Ema soovis, et kivi oleks õues. Ei lastel ega ka isal seda kivi ilma abivahenditeta liigutada ei õnnestunud. Kivi siiski saadi õue. Kivi teisaldamiseks kasutati kangi. Kangiks võeti latt, see suruti kivi serva alla. Väike kivi pandi kangi alla toetuspunktiks. Kui Veiko kangi ühele otsale vajutas, tõusis kivi serv veidi, kuid mitte piisavalt. Veiko otsis kangiks pikema lati, millega sai kivi teise kohta veeretada. Niimoodi, kangi abil, sai Veiko oma jõudu võimendada.

Füüsikas käsitatakse kangina paindumatut varrast, millele mõjuvat raskusjõudu ei arvestata. Käsitleme erijuhtu, kus kang ja sellele rakendatud jõud on omavahel risti.
Tähtsad punktid ja kaugused
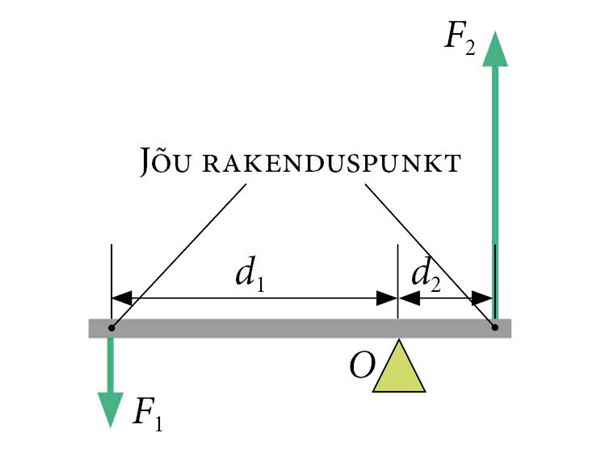
Kang saab pöörelda ümber toetuspunkti O.
Jõu mõjupunkti nimetatakse jõu rakenduspunktiks.
Jõu rakenduspunkti ja kangi toetuspunkti vahelist kaugust nimetatakse jõuõlaks (d).
Kangil on kaks jõu õlga.
Kangi tasakaal
Joonisel kujutatud kangi pikemale õlale d1 on rakendatud jõud F1. See jõud avaldab kangile pööravat toimet ja püüab kangi vasakut poolt pöörata allapoole. Selle tasakaalustamiseks peame mõjuma kangi teisele õlale d2 mingi jõuga F2, mis püüab kangi paremat poolt pöörata allapoole. Katsetamine erinevate koormistega näitab, et jõu pöörav toime sõltub lisaks jõule veel jõu õlast ning on võrdeline jõu ja jõu õla korrutisega Fd. Kangi tasakaalu korral on jõudude pööravad mõjud võrdsed, mis annab kangi tasakaalutingimuseks
F1d1 = F2d2.
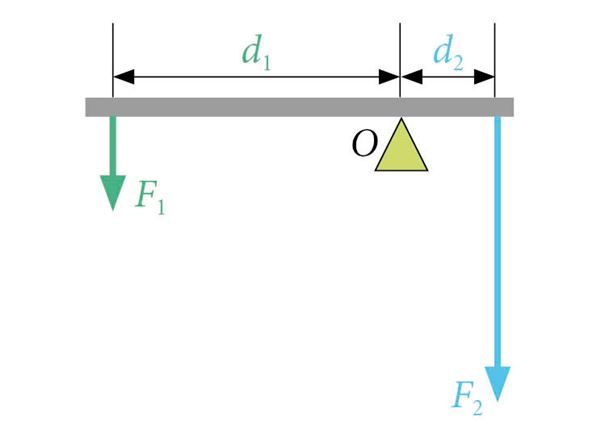
Jõu pööravat mõju iseloomustab jõu ja selle õla korrutis (Fd).
Kangi tasakaalu korral on jõudude pööravad mõjud võrdsed ja vastassuunalised.
Sellist tasakaalutingimust rakendatakse näiteks kangkaalude korral. Seal on kangi õlad võrdsed, d1 = d2, ja järelikult on kaalude tasakaalu korral võrdsed ka jõud, F1 = F2. Pannes ühele kaalukausile kaalutava eseme massiga m, mõjub sellele raskusjõud Fr = mg. Selle tasakaalustamiseks peame mõjuma teisele kausike täpselt sama suure raskusjõuga Fr = mg ja asetama teisele kausile kaaluvihte, mille kogumass oleks sama suur.

Kiigega kiikumisel kehtib sama kangi tasakaalutingimus, mistõttu peame arvestama seda, et inimesed võivad olla erineva massiga. Sama massiga inimeste korral peavad nad asetsema kiige kinnituspunktist samal kaugusel (jõu õlad on võrdsed). Erinevate masside korral peab aga suurema massiga inimene asetsema kinnituspunktile lähemal (jõu õlad on erinevad). Kiigel on mõjuvaks jõuks Maa külgetõmbejõud. Kuna see on aga võrdeline inimese massiga, siis saame tasakaalutingimuseks m1d1 = m2d2. Kui näiteks üks inimene on massiga 60 kg ja ta on kiige toetuspunktist 0,8 m kaugusel (jõu õlg d1 = 0,8 m), siis teisel pool olev 40 kg massiga inimene peaks olema kinnituspunktist 1,2 m kaugusel (jõu õlg d2 = 1,2 m).

Kangi kasutamine raskuste teisaldamiseks
Vaatame, kuidas Veiko kangiga kivi teisaldas. Veiko surus kangi kivi serva alla. Kivi surub kangi lühemale otsale oma raskusjõuga Fr. Selleks, et kivi tõsta, peame kivile mõjuma sama suure, kuid ülespoole suunatud jõuga F2 = Fr. Kui on tegemist raske kiviga, mida inimene tõsta ei jõua, tuleb lähtuda sellest, et jõu pöörav toime sõltub lisaks jõule veel jõu õlast. Kehtib sama tasakaalu tingimus
F1d1 = F2d2.
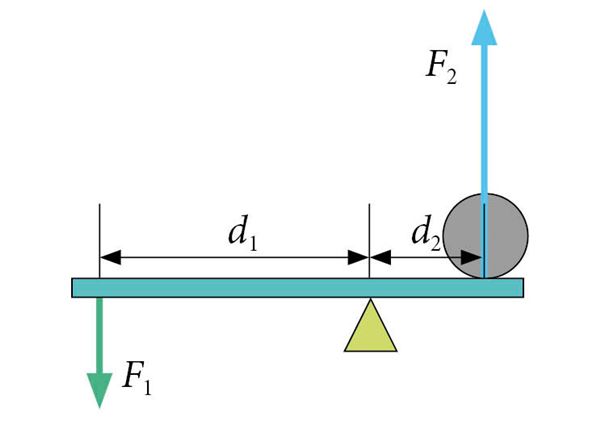
Kasutades pikemat jõu õlga, saame jõus võita (rakendada väiksemat jõudu) nii mitu korda, kui mitu korda pikema jõu õla me valime.
Oletame, et kivi mass, mida Veiko tahtis teisaldada, on 200 kg, mis tähendab, et kivile mõjuv raskusjõud on 2000 N ja kangi kivi alla toetuva otsa pikkus (jõu õlg d2) on 20 cm ehk 0,2 m. Oletame, et Veiko suudab kangi teisele otsale rakendada jõudu 200 N. Et avaldada sama suurt, kuid vastassuunalist pööravat toimet, peame valima kangi, millel teise õla pikkus oleks vastavalt kümme korda suurem, s.t d1 = 2 m.
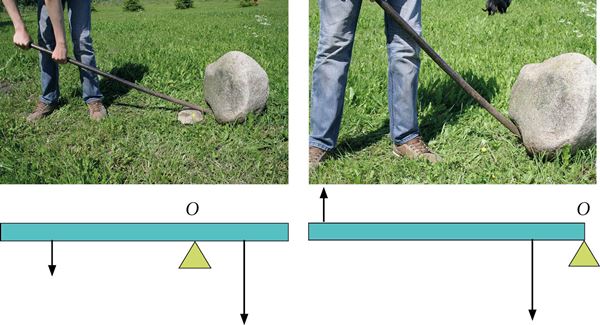
Kus on kangi toetuspunkt? | |
Kus on kangi jõu õlad? | |
Millises suunas tuleb avaldada kangile jõudu kivi kergitamiseks? | |
Milliseid jõudusid kujutavad joonistel olevad nooled?
Kang on lihtmehhanism
Mehhanism tähendab seadet, mis muundab ühe liikumise teiseks. Liht- tähendab, et antud mehhanism koosneb lihtsatest elementidest. Antud juhul on selleks paindumatu varras, mida me nimetame kangiks ja mingi ese, millele kang toetub. Lihtmehhanismid võeti kasutusele raskete esemete tõstmiseks ja liigutamiseks.
Näpitstangid
Tangid koosnevad kahest ühesugusest kangist, mis pöörlevad ühise ühenduspunkti ümber. Üheks õlaks on käepidemed, teiseks haarad. Käepidemeid kokku surudes rakendame kangi pikemale õlale jõudu. Jõud kandub üle haaradele. Haaradel rakenduv jõud on nii mitu korda suurem käepidemetele rakendatud jõust, kui mitu korda on haarad lühemad käepidemetest.
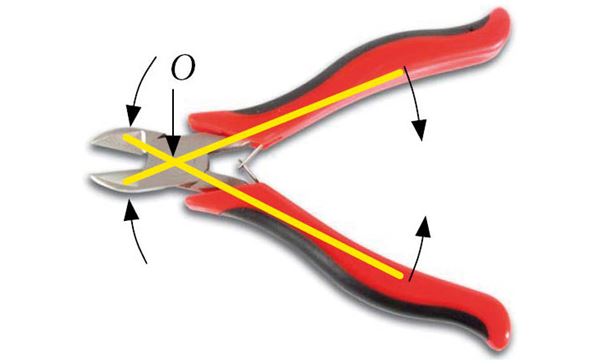
- kuni 3 korda
- 4–6 korda
- 7–9 korda
- üle 10 korra
Pean meeles
Kang on lihtmehhanism.
Jõu pööravat mõju iseloomustab jõu ja selle õla korrutis (Fd).
Kang on tasakaalus, kui kangile mõjuvate jõudude pööravad mõjud on võrdsed ja vastassuunalised: F1d1 = F2d2.
Küsimusi ja ülesandeid
- Vasta õppetüki alguses olevale küsimusele.
- Selgita kääride tööpõhimõtet.
- Millest lähtus Archimedes, kui ta ütles, et „Andke mulle piisavalt suur kang ja toetuspunkt, siis ma liigutan Maa paigast”? Selgita.
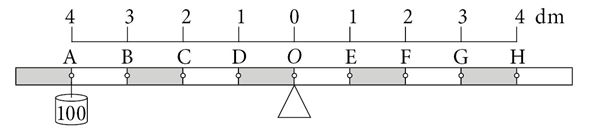
Kuhu tuleb riputada kaks sama massiga koormist, et kang oleks tasakaalus?
Mitu koormist tuleks riputada punkti E, et kang oleks tasakaalus?
