Arv e

Eelmises peatükis leidsime, et matemaatikas laialt kasutatav konstant π on esitatav teatud jada piir­väärtusena:

$$ \mathrm{\pi }=\underset{n\to \infty }{\lim }\left(n·\sin \frac{180°}{n}\right)$$.

On leitud veel mitmeid teisigi hääbuvaid jadasid, mille liikmete lõpmatu summa esitub arvu π kaudu:

$$ \frac{\mathrm{\pi }}{4}=\underset{n\to \infty }{\lim }\left[1-\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\dots +{\left(-1\right)}^{n-1}·\frac{1}{2n - 1}\right]$$

$$ \frac{{\mathrm{\pi }}^2}{6}=\underset{n\to \infty }{\lim }\left[1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{5^2}+\dots +\frac{1}{n^2}\right]$$

$$ \frac{{\mathrm{\pi }}^2}{8}=\underset{n\to \infty }{\lim }\left[1+\frac{1}{3^2}+\frac{1}{5^2}+\frac{1}{7^2}+\dots +\frac{1}{{\left(2n - 1\right)}^2}\right]$$.

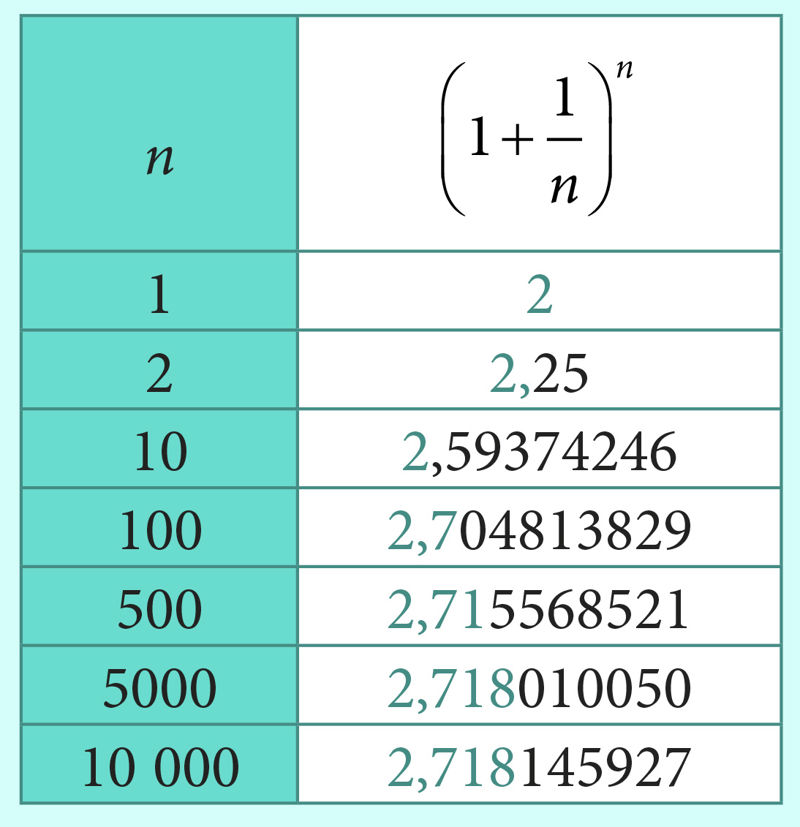Näeme, et järje­numbri n kasvades jääb jada liikmetel tõe­poolest järjest rohkem kümnend­kohti muutumatuks. Selle arvu 23 kümnend­kohta leidis Leonhard Euler, kes võttis ka vaadeldava arvu tähisena kasutusele tähe e. Arv e on irratsionaal­arv:

e = 2,7 1828 1828 4590 4523…

Seega

$$ e=\underset{n\to \infty }{\lim }{\left(1+\frac{1}{n}\right)}^n$$.

Selle konstandi kasutus­vald­kondadega tutvume lähemalt üle­järgmises teemas.