Tõenäosusteooria on matemaatika osa, mis uurib juhuslikke sündmusi, püüdes nende toimumises leida seaduspärasusi. Üheks vahendiks on seejuures sündmuse tõenäosuse mõiste.
Meenutame, mis on juhuslik sündmus.
Juhuslikuks sündmuseks nimetatakse sündmust, mis antud tingimuste korral võib toimuda, kuid võib ka mitte toimuda.
Järelikult on tõenäosusteoorias juhusliku sündmuse jaoks vaid kaks võimalust, see kas toimub või ei toimu. Kolmandat võimalust ei ole (nn välistatud kolmanda seadus). Reaalsuses on vahel asi keerulisem. Kui näiteks hommikul on trepp veepiiskadest märg, siis pole alati selge, kas ikka toimus sündmus „sadas vihma” või mitte.
Juhuslikuks sündmuseks on näiteks võitmine loteriil, 6 silma tulek täringu viskamisel, laskevõistlusel märklaua tabamine kümnesse.
Sündmusi tähistatakse lühema märkimise ja nimetamise huvides suurtähtedega A, B, jne või sümbolitega A1, A2, jne.
Üks ja sama juhuslik sündmus A võib tavaliselt toimuda mitmel erineval viisil. Näiteks kahe täringu (olgu need must ja valge) korraga viskamisel võib 5 silma tulla (loeme selle sündmuseks A) neljal erineval viisil. Need on 1 + 4, 2 + 3, 3 + 2, 4 + 1, kus esimene liidetav näitab tulemust mustal täringul, teine aga valgel täringul. Nimetatud üksikjuhud ehk sündmuse A jaoks soodsad juhud on võrdvõimalikud, sest pole põhjust, et mingi variant neist neljast tuleks teistest sagedamini esile. Võrdvõimalikest juhtudest 1 + 4, 2 + 3, 3 + 2, 4 + 1 igat võib vaadelda omaette sündmusena. Seetõttu nimetatakse neid ka sündmuse A jaoks soodsateks elementaarsündmuseks. Elementaarsündmused ei ole enam esitatavad erinevate üksikjuhtude kaudu.
Elementaarsündmusi tähistame edaspidi sümbolitega E1, E2, E3, …
Sündmuse A (5 silma tulek kahe täringu korraga viskamisel) soodsad juhud kuuluvad sündmuse A jaoks nn kõigi võimaluste hulka. Viimaseid on 36, sest nii mustal kui ka valgel täringul on erinevaid silmade arve 6. Ka need võimalused on võrdvõimalikud ega ole enam esitatavad erinevate üksikjuhtude kaudu. Kokkuvõtvalt: kahe täringu korraga viskamisel on 5 silma tulekuks kõiki võimalusi (kõiki elementaarsündmusi) 36 (1 + 1, 1 + 2, 1 + 3, …, 2 + 1, 2 + 2, …, 6 + 6), millest soodsaid juhte on 4.
Öeldakse, et elementaarsündmuste hulk {E1, E2, E3, …, En} on täielik ehk see moodustab elementaarsündmuste ruumi, kui igal katsel, näiteks täringu viskamisel, mingi neist elementaarsündmustest ikka esile tuleb, n on lõplik arv, ükski kaks elementaarsündmust ei saa korraga (samal katsel) esile tulla ja muidugi on täidetud võrdvõimalikkuse nõue. Elementaarsündmuste ruumi tähistatakse tavaliselt tähega U:
U = {E1, E2, E3, …En}.
Kui sündmuse jaoks on soodsad kõik tema üksikjuhud (elementaarsündmused E1, E2, E3, …, En), nimetatakse sündmust kindlaks sündmuseks. Järelikult toimub kindel sündmus antud tingimuste korral kindlasti.
Näiteks on sündmus, mis seisneb kas 1, 2, 3, 4, 5 või 6 silma tulekus täringu viskamisel kindel sündmus, sest iga täringuviske (katse) korral mingi silmade arv nendest ikka esile tuleb.
Kindlat sündmust tähistatakse tähega U või Ω.
Kui sündmuse V jaoks soodsad juhud puuduvad, nimetatakse sündmust V võimatuks sündmuseks. Võimatu sündmus ei toimu antud tingimuste korral kindlasti.
Nii on näiteks võimatu sündmus see, et täringu viskamisel tuleb 7 silma.
Võimatut sündmust tähistatakse tähega V või sümboliga ∅.
Sündmusi A ja B nimetatakse võrdseteks ning kirjutatakse A = B, kui nendel on samad soodsad juhud samade elementaarsündmuste E1, E2, E3, …, En seast.
Kui näiteks A tähendab paarisarvu silmade tulekut ja B kahega jaguva silmade arvu tulekut täringu viskamisel, siis A = B.
Sündmusi kujutatakse sageli geomeetriliselt, et paremini ilmestada nendevahelisi seoseid. Kui iga elementaarsündmust E1, E2, E3, …, En tähistab punkt tasandil (joon. 1.3), siis piirkond U, mis neid sisaldab, tähendab kindlat sündmust U. Juhuslikku sündmust A tähistab aga piirkond, mis sisaldab osa elementaarsündmustest. Võimatut sündmust V kujutame tasandist (piirkonnast U) väljaspool asuva osana, mis ei haara ühtegi elementaarsündmust tähistavat punkti.
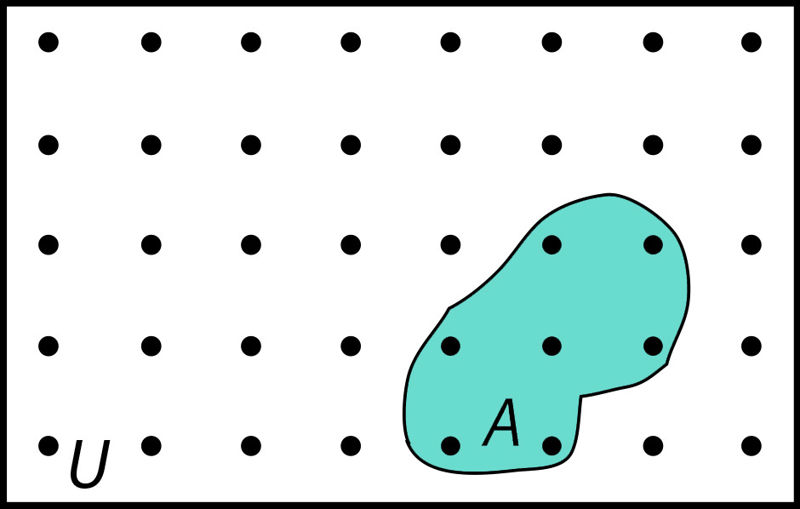
Joon. 1.3
|
||||||
Juhuslik sündmus A kas toimub või ei toimu. Mis toimub siis, kui sündmus A ei toimu? Sellisel juhul ei toimu ükski sündmuse A jaoks soodne juht (elementaarsündmusi tähistavad punktid valges piirkonnas joonisel 1.4), toimub aga mingi elementaarsündmus, mis ei ole soodus sündmuse A jaoks (punktid värvilises piirkonnas samal joonisel). See aga tähendab ühe teise sündmuse toimumist, mille soodsaid juhte tähistavad värvilise piirkonna punktid. Seda sündmust nimetatakse sündmuse A vastandsündmuseks ja tähistatakse sümboliga
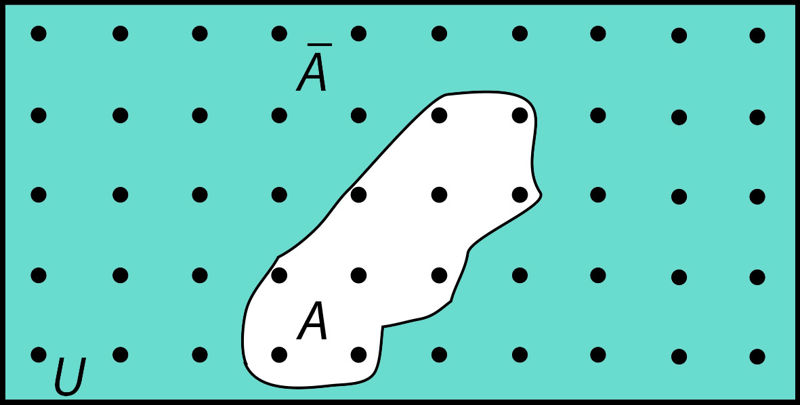
Joon. 1.4
|
||||||
Lühemalt:
sündmuse A vastandsündmuseks nimetatakse sündmust, mis toimub parajasti siis, kui sündmus A ei toimu.
Näide.
Loeme täringu viskamisel sündmuseks A kolmega jaguva silmade arvu (3 või 6 silma) tuleku. Sündmuse A vastandsündmuseks
Kindla sündmuse vastandsündmuseks loetakse võimatut sündmust, s.t
Ülesanded A
Ülesanne 65. Mündi viskamine
Kas need on võrdvõimalikud ja välistavad?
Nimetage sündmuse vapp jaoks soodsad võimalused.
Ülesanne 66. Kaardi tõmbamine pakist
Ülesanne 67. Kahe mündi viskamine
Ülesanne 68. Kuulide võtmine urnist
Ülesanne 69. Täringu viskamine
Ülesanne 70. Tähekaartide ladumine
Ülesanne 71. Sündmuse vastandsündmus
Ülesanne 72. Sündmuse vastandsündmus
Ülesanne 73. Sümboli tähendus
Millist sündmust võiks tähendada sümbol
Ülesanne 74. Sündmuse vastandsündmus
Mis on sündmus
Ülesanne 75. Sündmuse vastandsündmus
Ülesanne 76. Sündmuse vastandsündmus
- Mis on kordarvu silmade tuleku kui sündmuse K vastandsündmus?
