- Milleks kasutatakse lihtmehhanisme?
- Kas lihtmehhanismiga töötamisel tehakse vähem tööd kui selleta?
Liiikumatu ja liikuv plokk
Koolivaheajal külastas Paul oma onu. Garaažis märkas poiss mingit asjandust. Ta oli näinud seiklusmatkal, kuidas samasuguse asjaga kahe puu vahele trossi pingule tõmmati. Paul tahtis teada, mis see on ja milleks kasutatakse. Onu rääkis: „See on tali. Mina kasutasin tali varem autol mootori ära tõstmiseks. Praegu seisab niisama.”

Tali on lihtmehhanism, mis koosneb kahest ketaste plokist. Igal kettal on soon nööri või trossi jaoks. Kettad saavad pöörelda. Ühte plokki nimetatakse liikumatuks plokiks, teist liikuvaks plokiks. Liikumatu plokk on kinnitatud toele ega saa toe suhtes liikuda. Liikuv plokk liigub koos koormisega.
Selleks, et aru saada tali tööpõhimõttest, vaatame eraldi ploki tööpõhimõtet. See on liikumatu ja liikuva ploki korral erinev. Liikumatu plokiga saab muuta jõu suunda, liikuva plokiga saab muuta jõu suurust.
Liikumatu plokk
Liikumatu ploki korral on plokk jäigalt kinnitatud toele ja asetseb tõstetavast esemest kõrgemal. Liikumatut plokki kasutatakse jõu suuna muutmiseks, näiteks koormise tõstmiseks mugaval viisil.
Olgu meil vaja näiteks tõsta koormist, mille mõjub raskusjõud 500 N. Selleks peame tema tõstmiseks rakendama sama suurt ülespoole suunatud jõudu 500 N. Liikumatu plokiga tõstes peame nööri tõmbama samuti 500 N jõuga, sõltumata üle ploki oleva nööri suunast.
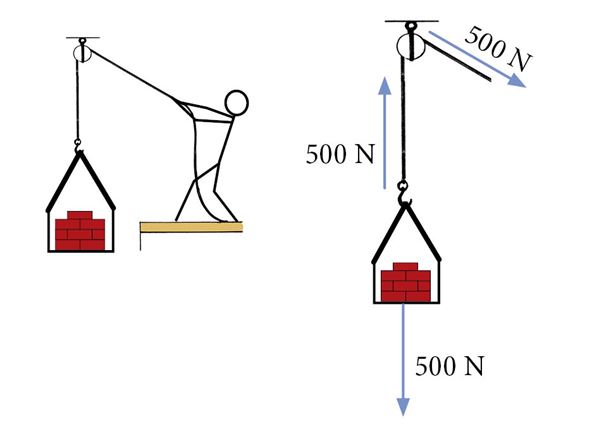
Liikuv plokk
Liikuva ploki korral on üks nööri ots jäigalt kinnitatud. Koormis on kinnitatud liikuva ploki külge. Koormise tõstmiseks peame rakendama jõudu üles suunatud nööri otsale.
Nüüd peame koormise tõstmiseks rakendama poole väiksemat jõudu. Olgu meil jälle koormise raskusjõuks 500 N. See jõud rakendub nööridele võrdselt (siin vaatame kahte nööriosa eraldi) ja me peame tõstmiseks rakendama jõudu 250 N.
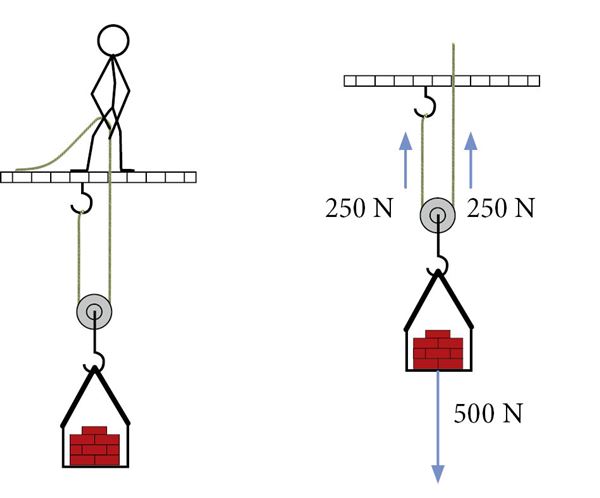
Mehaanika kuldreegel
Vanaisa laskis lastel tõsta plokkide abil maja lakka mõned pakid. Liikuva plokiga oli seda hoopiski kergem teha. „Mina tõstan liikuva plokiga, nii ma teen vähem tööd kui sina,” ütles Pilleriin Paulile. Vanaisa: „Sinu hüpotees on siis: koormise tõstmisel liikuva plokiga tehakse vähem tööd kui koormise tõstmisel samadel tingimustel liikumatu plokiga.” Kas sina oled Pilleriini hüpoteesiga nõus?
Järgnevalt kontrollime hüpoteesi teoreetiliselt. Katseliselt kontrolli hüpoteesi ise.
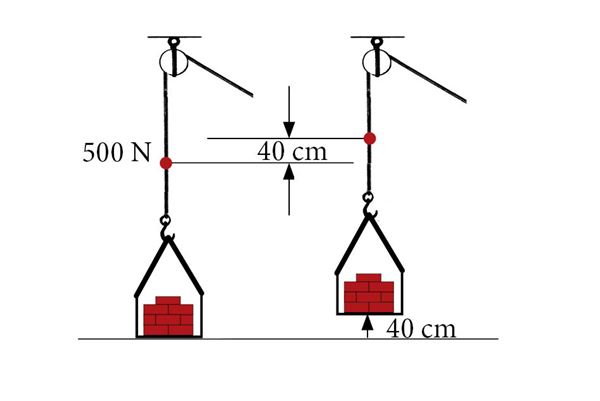
1. Töö koormise tõstmisel liikumatu plokiga
500-njuutonise koormise tõstmiseks on vaja rakendada jõudu 500 N. Tõusku koormis 40 cm = 0,4 m.
Nööri peab tõmbama ka 0,4 m. Tehtud töö (A = Fs) on A = 500 N · 0,4 m = 200 J.
Sama suur töö oleks tehtud ka siis, kui tõstmisel poleks plokki kasutatudki.
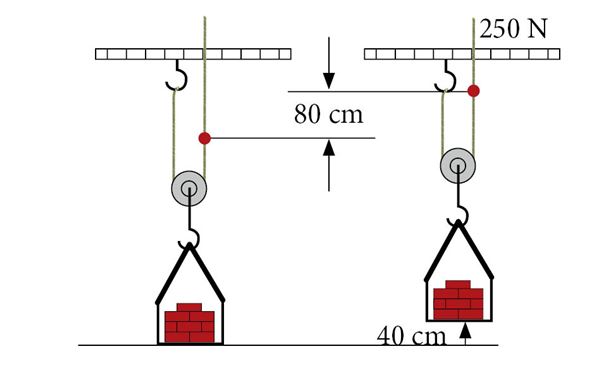
2. Töö koormise tõstmisel liikuva plokiga
500-njuutonise koormise tõstmiseks on vaja rakendada jõudu 250 N. Tõusku koormis 40 cm = 0,4 m.
Et koormis tõuseks 0,4 m, peab nööri tõmbama üles 0,8 m. Tehtud töö (A = Fs) on A = 250 N ∙ 0,8 m = 200 J.
Järeldus
Arvutused näitavad, et mõlemal juhul on koormise tõstmisel tehtud töö ühesugune. Seega, Pilleriini hüpotees ei ole õige. Samasuure koormise tõstmisel maast samale kõrgusele jääb tehtud töö samaks. See järeldub ka energia jäävuse seadusest, sest potentsiaalne energia sõltub kõrgusest. Samale kõrgusele tõstetud võrdse massiga koormustel on ühepalju potentsiaalset energiat, sõltumata sellest, millisel viisil koormust tõsteti.
Milles siis on erinevus liikumatu ja liikuva plokiga tõstmisel? Erinevus on selles, et liikuva ploki korral me rakendame kaks korda väiksemat jõudu, aga peame nööri üles tõmbama kaks korda kõrgemale. Nii palju, kui võidame jõus, kaotame nööri tõmbamisel teepikkuses.
Seda seaduspärasust, et lihtmehhanismidega me töös ei võida, küll aga võime võita jõus, teati juba vanal ajal. Igapäevase kogemuse põhjal tekkis reegel, mida nimetati mehaanika kuldreegliks:
nii palju, kui me võidame jõus, kaotame teepikkuses.
Tali
Kõige lihtsam tali koosneb liikumatust ja liikuvast plokist. Nüüd saame kasutada liikumatut plokki selleks, et pannes liikuvalt plokilt ületuleva nööri üle liikumatu ploki, ei pea me koormist tõstma otse üles, vaid võime muuta jõu mõjumise suunda. Kokkuvõttes me saavutame selle, et peame tõstmisel rakendama poole väiksemat jõudu ja tõstmisel tõmmata nööri meile sobivas suunas.
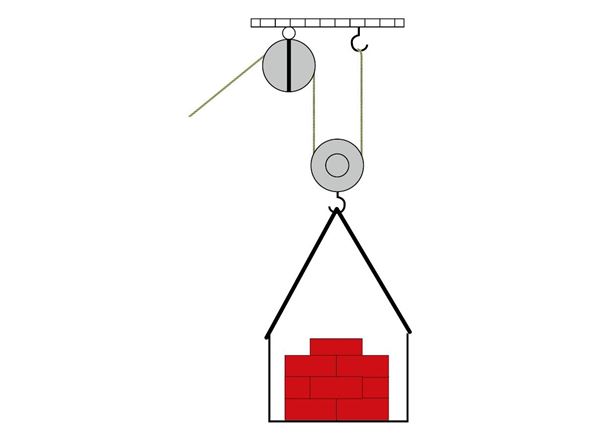
Milleks neid plokke kasutatakse?
plokiga muudetakse jõu mõjumise (tõmbamise) suunda.
plokiga saadakse võit jõus.

Veel lihtmehhanisme
Pöör
Kangile üsna sarnase tööpõhimõttega lihtmehhanism on pöör. Pööra moodustavad vänt ja võll. Vända pikkus on võlli raadiusest suurem. Ühe täispöörde tegemisel läbib käsi pikema tee kui ämber. Mida suurem on vända raadiuse ja võlli raadiuse suhe, seda kergem on ämbriga vett tõsta.
Veeämbri tõstmisel kaevust saame rakendada samasugust tasakaalutingimust, nagu kangi korral,
Frr = Fl,
kus Fr on veeämbrile mõjuv raskusjõud ja F vända otsale rakendatav jõud, r on võlli raadius ja l vända pikkus. Vända otsale rakendatav jõud on raskusjõust nii mitu korda väiksem, kui mitu korda on võlli raadius väiksem vända pikkusest.
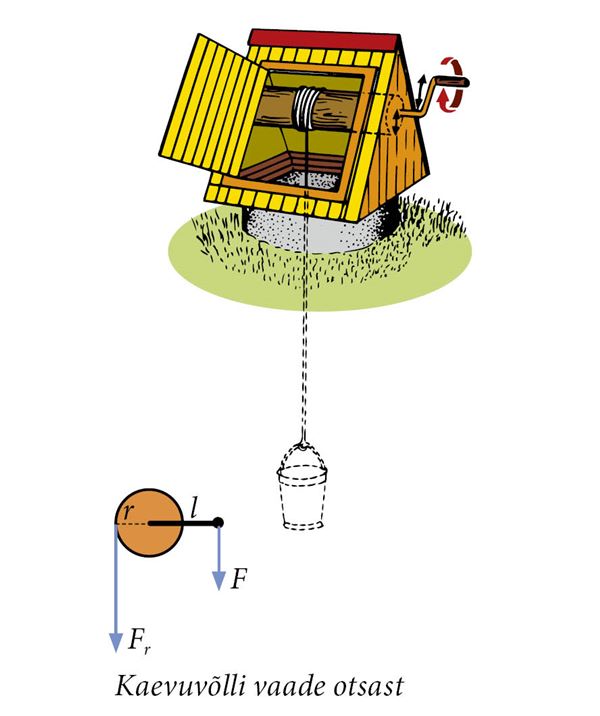
Olgu näiteks võlli raadius 10 cm ja kaevuvända pikkus 40 cm, siis 100 N raskusjõuga veeämbri tõstmiseks on vaja rakendada jõudu 25 N. Pööra korral kehtib samuti mehaanika kuldreegel, sest kui me võidame jõus neli korda, siis kaotame teepikkuses samuti neli korda – ühe täispöörde tegemisel läbib käsi neli korda pikema tee kui ämber.
Hammasratasülekanne
Paljudes masinates kasutatakse hammasratasülekannet, milles haakuvad erineva hammaste arvuga rattad. Joonisel kujutatud väikesel hammasrattal on 10 hammast, suurel 20. Kui väike ratas teeb kaks pööret, siis suur teeb ühe pöörde. Sellise ülekandega saab suurendada jõudu kahekordseks.

Hammasratasülekande eriliigiks on kettülekanne. Kettülekannet kasutatakse näiteks jalgrattas, kus keti abil ühendatakse eri suurusega ja seetõttu eri hammaste arvuga hammasrattad.
Ka auto käiguvahetussüsteem (käigukast) koosneb erineva suurusega hammasratastest. Käigu vahetamisel viiakse haakumisse erineva hammaste arvuga hammasrattad.
Kaldpind
Poisid lükkavad murutraktorit kaldteed mööda autosse. Kaldtee, mida füüsikas nimetatakse kaldpinnaks, on lihtmehhanism. Ka kaldpinna korral kehtib mehaanika kuldreegel. Kaldpinda kasutades võidetakse jõus nii mitu korda, kui mitu korda on kaldpinna pikkus suurem kõrgusest.


- Kaldpinnaga ei saa võita jõus.
- Umbes 2 korda.
- Umbes 4 korda.
- Umbes 10 korda.
Kõndides trepist või sõites autoga serpentiini (fotol kujutatud looklev mägitee) mööda mäkke, saab rakendada väiksemat jõudu, kui on raskusjõud. Sel juhul tuleb läbida oluliselt pikem teekond.

Kaldpinna erijuhuna vaadeldakse ka kruvi.

Miks pole igiliikur võimalik?
Kokkuvõtteks võime öelda, et lihtmehhanismide abil ma saame tõsta ja teisaldada esemeid, mida me ise tõsta ei jõua. Lihtmehhanismiga saame rakendada väiksemat jõudu, aga peame selle arvel kaotama sama arv kordi teepikkuses. Kõikidel juhtudel võime öelda, et lihtmehhanismidega me kunagi töös ei võida, tehtud kogutöö jääb samaks. See tuleb energia jäävuse seadusest. Kui see nii ei oleks, saaks me ehitada masina, mis teeks tööd ilma lisaenergiat kulutamata. Sellist masinat nimetatakse igaveseks jõumasinaks ehk igiliikuriks.
Vaatame siin lihtsat näidet kaldpinnaga. Oletame, et raskuse tõstmiseks mingile kõrgusele h me teeme töö A, aga sama raskuse tõstmiseks kõrgusele h mööda kaldpinda teeme väiksema töö A' (kasutame ju väiksemat jõudu). Niisugusel juhul saaksime kasulikku tööd mitte millestki, sest tõstes raskuse kõrgusele h mööda kaldpinda ja lastes sellel sealt alla kukkuda, teeks kukkuv raskus rohkem tööd, kui tehti selle tõstmiseks. Nagu juba öeldud, ei ole see kooskõlas energia jäävuse seadusega.
Pean meeles
Lihtmehhanismideks on kang, liikuv plokk, pöör, kaldpind.
Lihtmehhanismide korral kehtib mehaanilise energia jäävuse seadus: ükski lihtmehhanism ei anna võitu töös.
Nii palju, kui me võidame jõus, kaotame teepikkuses.
Küsimusi ja ülesandeid
- Vasta õppetüki alguses olevatele küsimustele.
- Tee kindlaks, milliseid lihtmehhanisme on kasutatud jalgrattas.
- Kuidas tõestada, et lihtmehhanismidega töötamisel energiat säästa ei saa?
