Reaalarvulise astendajaga aste

Tuletame meelde, et reaalarvu a ∈ R korral:

a⁰ = 1, kui a ≠ 0

a¹ = a

aⁿ = a · a · a · ... · a (n tegurit) kui n ∈ {2; 3; 4; …}

$a^{- k} = \frac{1}{a^{k}}$ , kui a ≠ 0 ja k ∈ Z või a > 0 ja k ∈ Q

$a^{\frac{m}{n}} = {\begin{cases} \sqrt[n]{a^{m}}, kui a > 0, m \in Z ja n \in Z^{+} \\ 0, kui a = 0, m \in Z^{+} ja n \in Z^{+} \end{cases}$

Näide 1.

2,603⁰ = 1
8675¹ = 8675
3⁶ = 3 · 3 · 3 · 3 · 3 · 3 = 729
(–0,7)³ = (–0,7) · (–0,7) · (–0,7) = –0,343
4^{-2} = \frac{1}{4^2} = \frac{1}{16} = 0,0625

10,1^{\frac{3}{4}} = \sqrt[4]{10,1^3} = \sqrt[4]{1030,301} ≈ 5,66553635
\left(\frac{1}{27}\right)^{-\frac{2}{3}} = 27^{\frac{2}{3}} = \sqrt[3]{27^2} = 9
0^7,5 = 0

Kõigi nende korral on astendajaks ratsionaalarv, mille üldkuju on \frac{m}{n}, kus m ∈ Z ja n ∈ Z⁺. Tõepoolest, ka täisarv on esitatav , m=\frac{m}{1}.Niisiis tunneme seni ratsionaalarvuliste astendajatega (u ∈ Q, v ∈ Q) astmeid. Nende korral kehtivad valemid, kui a > 0 ja b > 0,

a^{u} \cdot a^{v} = a^{u + v}

$a^{u} : a^{v} = a^{u - v}$

${(a^{u})}^{v} = a^{u v}$

${(a b)}^{u} = a^{u} b^{u}$

${(\frac{a}{b})}^{u} = \frac{a^{u}}{b^{u}}$

(1)

Selgitame järgnevalt astme a^r tähendust, kui astendaja r on irratsionaalarv ja a > 0, a ∈ R.

Alustame konkreetsest näitest: millist arvu tähendab aste 5^{\sqrt{2}}?Irratsionaalarvu \sqrt{2} puuduga võetud kümnendlähendid moodustavad jada1; 1,4; 1,41; 1,414; 1,4142; 1,41421; 1,414213; 1,4142135; …Tähistame selle jada üldliikme sümboliga r_n. Kui nüüd n\to∞, siis r_n\to\sqrt{2} ehk lühemalt $\lim_{n \to \infty} r_{n} = \sqrt{2}$ . Arvu 5 vastavad astmed annavad aga jada

5¹; 5^1,4; 5^1,41; 5^1,414; 5^1,4142; 5^1,41421; 5^1,414213; 5^1,4142135; …,

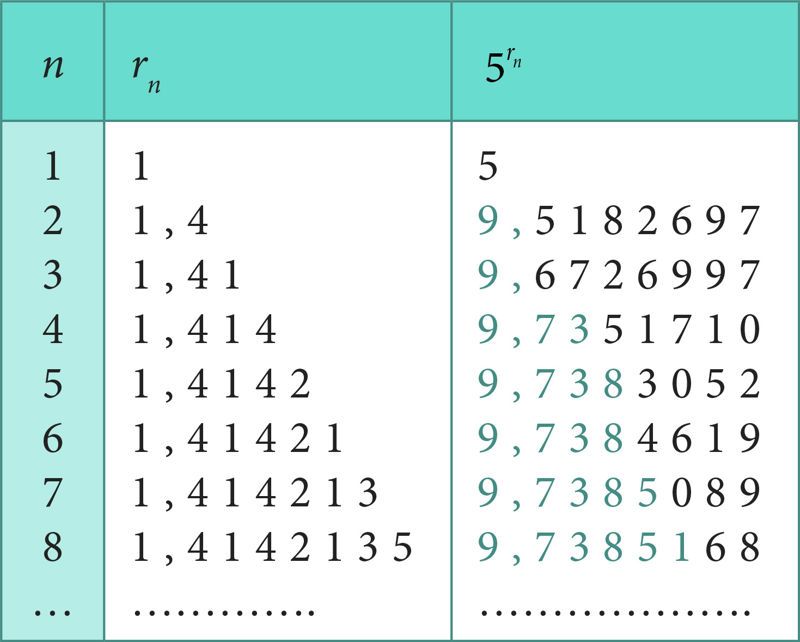
mille üldliige a_n=5^{r_n}. Et selle jada liikmed on ratsionaalarvuliste astendajatega astmed, siis teame, et neil on arvu tähendus ning me saame neid arvutada. Tulemused on järgmise tabeli kolmandas veerus.

Kolmanda veeru põhjal võib arvata, et jadas järjest kaugemale minnes jääb jada liikmetes järjest rohkem kümnendkohti (värvilised) muutumatuks. See viib mõttele, et jada 5¹; 5^1,4; 5^1,41; 5^1,414; …; 5^{r_n}; … väärtused lähenevad mingile arvule (jadal on piirväärtus), kui n\to∞.

Nii ka tegelikult on, eksisteerib selline arv

\lim_{n \to \infty} 5^{r_{n}}

. Seda loetaksegi 5^{\sqrt{2}} väärtuseks, s.t

5^{\sqrt{2}} = \lim_{n \to \infty} 5^{r_{n}}

. Millisele arvule 5^{r_n} väärtused n tõkestamatul kasvamisel lähenevad, lühemalt öeldes, millega piirväärtus

\lim_{n \to \infty} 5^{r_{n}}

täpselt võrdub, ei ole tegelikult oluline. Tähtis on, 1) et see arv on olemas (vastasel juhul puuduks kirjutisel 5^{\sqrt{2}} mõte) ja 2) et me saame kõnealuse arvu (järelikult ka 5^{\sqrt{2}} väärtuse) leida vastavalt vajadusele kui tahes suure täpsusega. Nii näiteks võime tabeli kolmanda veeru andmete põhjal (üldliikmega a_n=5^{r_n} antud jada liikmed) kirjutada, et täpsusega 0,05 on 5^{\sqrt{2}}=9,7, täpsusega 0,005 on 5^{\sqrt{2}}=9,74, täpsusega 0,0005 on 5^{\sqrt{2}}=9,739.Analoogiliselt saame tähenduse anda igale astmele a^r, kus a on positiivne reaalarv ja r on positiivne irratsionaalarv. Seejuures on võimalik a^r väärtust arvutada kui tahes täpselt.Kui astendaja on negatiivne irratsionaalarv –r (r > 0), siis defineeritakse, et

a^{- r} = \frac{1}{a^{r}}

Näide 2.

5^{-\sqrt{2}}=\frac{1}{5^{\sqrt{2}}}\approx\frac{1}{9,739} ≈ 0,1027

Kokku võttes oleme juhul a > 0 defineerinud astme a^r nii ratsionaalarvulise kui ka irratsionaalarvulise astendaja, s.t iga astendaja r korral. Seejuures jäävad kehtima seosed (1).

Näide 3.

4^{\sqrt{3}}\cdot4^{2\sqrt{3}} = 4^{\sqrt{3}+2\sqrt{3}} = 4^{3\sqrt{3}} = \left(4^3\right)^{\sqrt{3}} = 64^{\sqrt{3}}
3^{7+\sqrt{5}}:\ 3^{5+\sqrt{5}} = 3^{7+\sqrt{5}-\left(5+\sqrt{5}\right)} = 3^2 = 9
\left(2^{\sqrt{3}}\right)^{\sqrt{6}} = 2^{\sqrt{3}\cdot\sqrt{6}} = 2^{\sqrt{18}} = 2^{3\sqrt{2}} = \left(2^3\right)^{\sqrt{2}} = 8^{\sqrt{2}}
2^{\sqrt{7}}\cdot5^{\sqrt{7}} = \left(2\cdot5\right)^{\sqrt{7}} = 10^{\sqrt{7}}
12^{\sqrt{2}}:\ 4^{\sqrt{2}} = \left(\frac{12}{4}\right)^{\sqrt{2}} = 3^{\sqrt{2}}

Kehtivad ka astmete võrdsusest tulenevad järeldused (a > 0, u, v ∈ R):

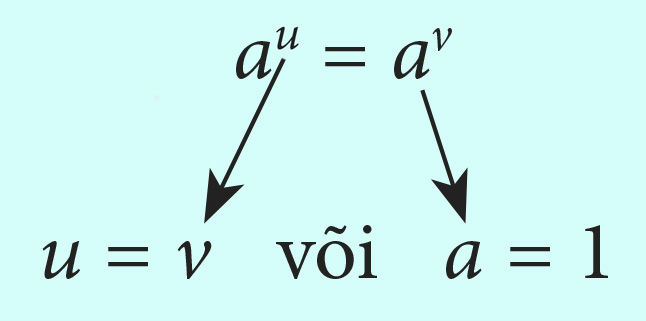Näide 4. Võrrandi 7^x = 343 lahendamiseks kirjutame selle kujul 7^x = 7³, millest x = 3.

Näites 4 lahendatud võrrand on eksponentvõrrand, s.t võrrand, kus tundmatu esineb vaid astendajas. Nendega tutvume põhjalikumalt hiljem.Oluliselt keerulisemaid võrrandeid saab lahendada järgneva põhjal (a > 0, b > 0, u ∈ R):

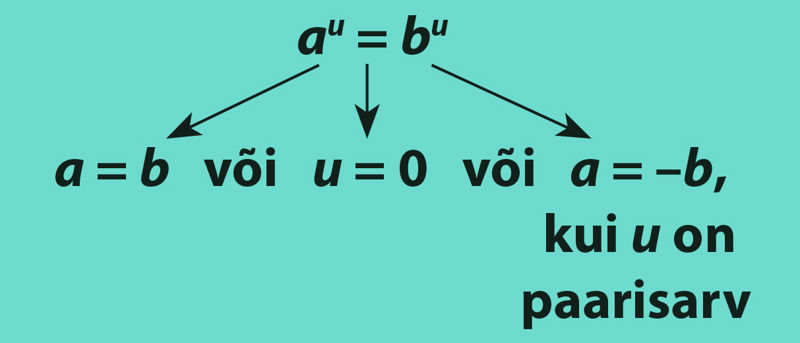Näide 5. Lahendame võrrandi (x – 6)⁴ = 16. Vaadeldavat võrrandit saab lahendada mitut moodi:

Võrrandile saab anda kuju (x – 6)⁴ = 2⁴, millest x – 6 = 2 ehk x₁ = 8 või x – 6 = –2 (sest astendaja on paarisarv) ehk x₂ = 4. Mõlemad lahendid sobivad.
Antud võrrandi saab lahendada ka juurimise teel. Siis x-6=\pm\sqrt[4]{16} ehk x – 6 = ±2, millest x₁ = 8, x₂ = 4.
Kirjutades antud võrrandi kujul (x – 6)⁴ – 4² = 0, saame võrrandi vasaku poole teisendada korrutiseks: [(x – 6)² – 4] · [(x – 6)² + 4] = 0.Nüüd (x – 6)² – 4 = 0 või (x – 6)² + 4 = 0. Esimesest võrrandist saame lahendid 8 ja 4, teisel võrrandil lahendid puuduvad.
Kui esialgses võrrandis avada sulud, saame täieliku neljanda astme võrrandi, mille lahendamine on oluliselt keerulisem.

Näide 6. Lahendame võrrandi (x – 6)^x = 2^x. Kasutame astmete võrdsusest tulenevaid järeldusi: x – 6 = 2 ⇒ x₁ = 8; kui x on paarisarv, siis võib olla ka x – 6 = –2 ⇒ x₂ = 4; kui astendaja x = 0, siis saame lisaks x₃ = 0. Kõik leitud x väärtused rahuldavad esialgset võrrandit, s.t on selle lahendid. Seega oleme leidnud meile täiesti tundmatut tüüpi võrrandi kolm lahendit.

Kasulik on veel teada teoreemi:

kui 0 < a < 1, siis $a^{r_{1}} > a^{r_{2}} \Leftrightarrow r_{1} < r_{2}$ ;

kui a > 1, siis $a^{r_{1}} < a^{r_{2}} \Leftrightarrow r_{1} < r_{2}$ .

Näide 7.

0,8^{\sqrt{2}}>0,8^{\sqrt{3}}, sest \sqrt{2}<\sqrt{3} ja a=0,8<1.
2,6^5<2,6^{\sqrt{26}}, sest 5<\sqrt{26} ja a=2,6>1.

Näide 8. Lahendame võrratused 1) 0,6^x > 0,6⁵ ja 2) 1,3^x+1 < 1,3².

Et astme alus a = 0,6 < 1, siis suuremale astmele vastab väiksem astendaja. Seega, x < 5.
Et a = 1,3 > 1, siis suuremale astmele vastab suurem astendaja: x + 1 < 2 ⇒ x < 1.

Astme a^r, kus a > 0 ja r ∈ R väärtuse arvutamiseks taskuarvutil on klahv x^y (vahel y^x või a^x) või klahv ∧. Sõltuvalt arvutist tuleb siis a^r leida kas skeemia x^y r = või r x^y a = või siis skeemi a ∧ r = järgi.

Näide 9. 2,5^1,8 ≈ 5,2035, arvutusskeem: 2,5 x^y 1,8 = või 2,5 ∧ 1,8 =; 0,3^–7 ≈ 4572,4737, arvutusskeem: 0,3 x^y 7 +/– = või 0,3 ∧ 7 +/– =.

Avaldiste a^{\sqrt{b}} ja a^{\frac{1}{c}} väärtusi saab arvutada vastavalt skeemide järgia x^y b √ = ja a x^y c 1/x =või a ∧ b √ = ja a ∧ ( 1 ÷ c ) =.Vaid väheste arvutite korral tuleb eelnevalt leida \sqrt{b} või vastavalt \frac{1}{c} ning viia see mällu, kust see siis õigel ajal jälle tabloole tuua.Kui arvutil on klahv x^1/y või ^y√x (vahel ^x√y), saab a^{\frac{1}{c}} ehk \sqrt[c]{a} väärtust arvutada lühemalt:a x^1/y c = või a ^y√x c = või c ^y√x a =.

Näide 10. 3^{\sqrt{2}}\approx4,7288, arvutusskeem 3 x^y 2 √ =,\sqrt[5]{4}=4^{\frac{1}{5}}\approx1,3195, arvutusskeem 4 x^y 5 1/x = või 4 x^1/y 5 =.

Avaldise a^{\frac{m}{n}} ehk \sqrt[n]{a^m} väärtuse arvutamiseks sobivad arvutusskeemid:

a x^y ( m ÷ n ) =,a x^y m a b/c n =,

a x^y m = x^y n 1/x =,m ÷ n M a x^y MR =.

Kui arvutil on astendamise klahv ∧, saab arvutada skeemi järgia ∧ ( m ÷ n ) =.

Näide 11. 1,7^{\frac{2}{3}}\approx1,4244, mille saame arvutada mitmeti:

1,7 x^y ( 2 ÷ 3 ) =1,7 x^y 2 a b/c 3 =1,7 x² x^y 3 1/x =

1,7 ∧ ( 2 ÷ 3 ) =1,7 x^y 2 = x^y 3 1/x =2 ÷ 3 M 1,7 x^y MR =

Astme 10^r leidmiseks on arvutil klahv 10^x ning vastav arvutusskeem on r 10^x. Näiteks arvutades skeemi järgi 3,04 10^x saame, et 10^3,04 ≈ 1096,4782.

Еще на эту тему

Ülesanded A

Ülesanne 543. Reaalarvulise astendajaga aste

Avaldis	c^5	c^8	c^{11}	c^1
Arvu c lubatavad väärtused

Avaldis	\left(c+3\right)^1	\left(c-5\right)^1	c^{10}	\left(c-8\right)^0
Arvu c lubatavad väärtused

Avaldis	\left(-c\right)^0	c^{-4}	c^{-3}	c^{-1}
Arvu c lubatavad väärtused

Avaldis	c^{\frac{3}{4}}	c^{\frac{1}{8}}	c^{\frac{1}{3}}	c^{-\frac{3}{8}}
Arvu c lubatavad väärtused

Ülesanne 544. Astendamine

4^3 =

\left(-4\right)^3 =

-4^3 =

5^0 =

-5^0 =

\left(-5\right)^0 =

0^6 =

0^1 =

0^0 =

3,2^1 =

1^{18} =

-7^1 =

\left(-1\right)^9 =

\left(-1\right)^7 =

\left(-1\right)^{2n+1} =

\left(-1\right)^{2n-1} =

\left(-1\right)^4 =

-1^4 =

\left(-1\right)^{28} =

\left(-1\right)^{2n} =

Ülesanne 545. Astendamine

2^{-3} =

5^{-1} =

6^{-2} =

2,5^{-1} =

0,25^{-2} =

0^{-3} =

1^{-7} =

\left(-2\right)^{-3} =

\left(-10\right)^{-2} =

-4^{-2} =

\left(-1\right)^{-6} =

\left(-5\right)^{-3} =

\left(\frac{1}{2}\right)^{-3} =

\left(\frac{1}{3}\right)^{-4} =

\left(\frac{2}{3}\right)^{-2} =

\frac{1}{3^{-2}} =

\frac{2}{5^{-3}} =

\frac{9}{2^{-4}} =

\frac{2}{2^{-3}} =

\frac{5}{1^{-4}} =

Ülesanne 546. Astendamine

4^{\frac{1}{2}} =

0,25^{\frac{3}{2}} =

125^{-\frac{2}{3}} =

0,0625^{0,75} =

16^{0,125} =

9^{-0,5} =

-16^{\frac{1}{4}} =

\left(-16\right)^{\frac{1}{4}} =

0^{\frac{2}{7}} =

1^{\frac{4}{9}} =

-8^{\frac{1}{3}} =

0^{-2,4} =

Ülesanne 547. Tehted astmetega

2^{1,5}\cdot2^{2,5} =

4^{2,8}\cdot4^{0,2} =

3^{5,4}\cdot3^{-2,4} =

1,8^7:\ 1,8^5 =

\left(-0,4\right)^9\ :\ \left(-0,4\right) =

3^{-6\ }:\ 3^{-4} =

\left(4^{\frac{5}{12}}\right)^6 =

\left(2^{-\frac{4}{7}}\right)^{14} =

\left(3^{0,25}\right)^8 =

\left(7\cdot3\right)^2 =

\left(25\cdot49\right)^{\frac{1}{2}} =

\left(8\cdot27\right)^{\frac{2}{3}} =

\left(\frac{8}{125}\right)^{\frac{1}{3}} =

\left(\frac{1}{2}\right)^{-4} =

\left(\frac{1}{64}\right)^{\frac{2}{3}} =

Ülesanne 548. Lihtsustamine

a^7\cdot a^3 =

b^{-2}\cdot b^6 =

c^{-0,4}\cdot c^{-2,8} =

k^n\cdot k^{8-n} =

r^0\cdot r^{-1} =

m^{4n}\cdot m^n =

a^4:\ a^3 =

a^{-3,2}:\ a^{-1,2} =

a^{-1}:\ a^0 =

\left(p^{-5}\right)^4 =

\left(q^0\right)^{-5} =

\left(r^{-0,5}\right)^7 =

2n\cdot4n^{-3} =

12a^5:\ 10a^{-5} =

\left(8r^{-3}\right)^{\frac{4}{3}} =

Ülesanne 549. Tehted astmete ja juurtega

\sqrt[3]{4}:\sqrt[6]{2} =

9^{-\frac{5}{2}}\cdot\sqrt[3]{27} =

\left(\sqrt[8]{64}\right)^{\frac{4}{15}} =

\sqrt[3]{a^2}:\sqrt[6]{a^3} =

a^{-5}\cdot\sqrt[3]{a^{0,3}} =

\left(\sqrt[7]{a}\right)^0 =

\sqrt{5}:\sqrt[4]{25} =

\sqrt[3]{8^{-3}}\cdot2^3 =

Ülesanne 550. Lihtsustamine

\sqrt[5]{a^2}:\sqrt[15]{a^4}\cdot a^{\frac{3}{15}} =

\left(a^{\frac{1}{6}}-b^3\right)\left(a^{\frac{1}{6}}+b^3\right) =

\left(\sqrt[4]{9}+8^{\frac{1}{3}}\right)\left(\sqrt[4]{9}-8^{\frac{1}{3}}\right) =

\left(a^{\frac{8}{7}}+a^{-\frac{4}{7}}\right)a^{\frac{7}{2}} =

\left(x^{\frac{1}{3}}-c^{-1}\right)\left(x^{\frac{1}{3}}+c^{-1}\right) =

\left(a^{0,5}-2\sqrt{a}\right)^2 =

Ülesanne 551. Lihtsustamine

\left(5^{\sqrt{2}}\right)^{\sqrt{2}} =

4^{\sqrt{3}}:\ 4^{\sqrt{3}-2} =

2^{\sqrt{3}}\cdot2^{\sqrt{2}} =

\left(2^{\sqrt{6}}\right)^{\sqrt{3}} =

5^{\sqrt{12}}\cdot5^{\sqrt{3}}\cdot5^{\sqrt{27}} =

3^{\sqrt{5}}\cdot3^{-3\sqrt{5}} =

2^{\sqrt{3}}\cdot5^{\sqrt{3}} =

2^{3\cdot2^{0,5}}:2^{2^{0,5}} =

10^{\sqrt{7}}:\ 2^{\sqrt{7}} =

7^{\sqrt{5}}\cdot7^{-\sqrt{5}} =

2^{\sqrt{2}}:\ 16^{-\sqrt{2}} =

10^{2\sqrt{2}}:\ 25^{2\sqrt{2}} =

Ülesanne 552. Eksponentvõrrandi lahendamine

2^x=16

x =

3^x=27^{-1}

x =

5^{-x}=25

x =

\sqrt[4]{4}=8^x

x =

9\cdot3^x=27^{-x}

x =

0,125^x=2^{4x}

x =

5^x=25^{\sqrt{2}}

x =

4^{\sqrt{2}}=2^{x+\sqrt{2}}

x =

6^{x+\sqrt{2}}=1

x =

5^{x+1}=0

x =

3^{x^2-4}=1

x = või x =

7^{x-8}=-1

x =

Ülesanne 553. Reaalarvulise astendajaga aste

${(- 2)}^{- 10}$
$6^{0,6}$
$0^{4}$
$1^{- 5}$
${(- 7)}^{0}$
${(- 3)}^{1}$
$- 3^{2}$
${0,8}^{- 4}$

$6^{0,6}$
$1^{- 5}$
$- 3^{2}$
$0^{4}$
${(- 2)}^{- 10}$
${(- 7)}^{0}$
${(- 3)}^{1}$
${0,8}^{- 4}$

Ülesanne 554. Reaalarvulise astendajaga aste

2^4 =

5^{2,4} =

1,038^{10} =

2753^{0,35} =

2^{-3} =

4^{-6,2} =

2,13^{-6} =

9009^{-0,7} =

2^{\sqrt{16}} =

5^{\sqrt{9,3}} =

1,1^{\sqrt{476}} =

6,6^{\sqrt{63,9992}} =

9^{\frac{1}{2}} =

77^{\frac{1}{9}} =

25^{\frac{1}{10}} =

32\ 086^{\frac{1}{4}} =

Ülesanne 555. Reaalarvulise astendajaga aste

\pi^4 =

2^{\pi} =

\pi^{\pi} =

5^{-\pi} =

-3,3^5 =

\left(-3,3\right)^5 =

\left(-0,72\right)^8 =

-1,3^{2,9} =

Ülesanne 556. Reaalarvulise astendajaga aste

10^7 =

10^{1,09} =

10^{-5,3} =

10^{18,04} =

10^{\pi} =

10^{\sqrt{5}} =

\sqrt[7]{10} =

\sqrt[13]{10^4} =

Еще на эту тему

Ülesanded B

Ülesanne 557. Lihtsustamine

\sqrt[3]{a^2}:\sqrt[6]{a} =

a^{-5}\cdot\sqrt[3]{a^{0,3}} =

\left(\sqrt[8]{a^3}\right)^{\frac{4}{21}} =

Ülesanne 558. Tehted astmete ja juurtega

\left(4^{\frac{3}{4}}-2^{-0,5}\right)^2 =

3^{-0,25}\cdot81^{0,125}\cdot9^{\frac{3}{2}} =

\sqrt[3]{4}:\ 0,5^{-3}\ :\ 2^{-3} =

\left[3\cdot2^{-2}-\left(\frac{2}{3}\right)^{-1}\right]^{-1} =

\left[4^{-\frac{1}{4}}+\left(2^{1,5}\right)^{-\frac{4}{3}}\right]\cdot4^{-0,25} =

\left(23^0\right)^2-7,5\left(\sqrt[4]{4^{-3}}\right)^2 =

Ülesanne 559. Võrdlemine

20³ 30³

(–2)⁷ (–3)⁷

(–0,1)⁵ (–0,3)⁵

0,5⁴ 0,8⁴

(–2)¹⁰ (–3)¹⁰

(–0,2)⁴ (–0,3)⁴

(–8)⁶ 8⁶

–5⁴ (–5)⁴

2^0,5 3^0,5

Ülesanne 560. Võrdlemine

3^{\sqrt{2}} 3^{\sqrt{3}}

10^{0,5} \sqrt{10}

0,3^{1,5} 0,3^{\sqrt{2}}

7^{4\sqrt{3}} 7^{\sqrt{5}}

16^{-0,5} 2^{-\sqrt{2}}

0,16^{-\sqrt{2}} 0,4^{-\sqrt{3}}

Kui a>1, siis a^{\sqrt{2}} a^{\sqrt{3}},

kui a=1, siis a^{\sqrt{2}} a^{\sqrt{3}},

kui 0<a<1, siis a^{\sqrt{2}} a^{\sqrt{3}}.

Kui a>1, siis a^{-\sqrt{5}} a^{-\sqrt{7}},

kui a=1, siis a^{-\sqrt{5}} a^{-\sqrt{7}},

kui 0<a<1, siis a^{-\sqrt{5}} a^{-\sqrt{7}}.

Ülesanne 561. Eksponentvõrratuse lahendamine

4^x<4^3
x

2^{2x}\le4
x

125^x>5^{4,5}
x

\left(\frac{1}{2}\right)^x>\left(\frac{1}{2}\right)^5
x

0,3^{x+1}>0,3
x

0,1^{2x}\le0,01
x

3^{0,1}\ge3^{4x+1}
x

8^{0,5}<2^{x+1}
x

\left(\frac{2}{3}\right)^x>5\cdot3^{-2}
x

3^x<3^{\sqrt{2}}
x

1^x\le1^{\sqrt{5}}
x

\left(\frac{5}{3}\right)^x>\left(\frac{5}{3}\right)^{2+\sqrt{2}}
x

-4^x<16
x

5^x<-125
x

2^x>5^0
x

Ülesanne 562. Võrdlemine

2^2 2^5

2^{-2} 2^{-3}

2^{-10} 2^4

2^0 2^{-1}

3^{\frac{1}{3}} 3^{\frac{1}{2}}

3^{\frac{1}{3}} 3^{-\frac{1}{2}}

3^{-\frac{1}{3}} 3^{-\frac{1}{2}}

64^{\frac{2}{3}} 64^{\frac{7}{2}}

0,5^2 0,5^5

0,5^{-2} 0,5^{-3}

0,5^{-10} 0,5^4

0,5^n 0,5^m; n>m; n, m ∈ N

10^n või 10^m; n, m ∈ Z

Kui n<m, siis 10^n 10^m ja
kui n>m, siis 10^n 10^m.

a^n või a^m; a > 1; n, m ∈ Z

Kui n<m, siis a^n a^m ja
kui n>m, siis a^n a^m.

Ülesanne 563. Reaalarvulise astendajaga aste

0,5^5

2^{0,05}

a^6

a^5

0,5^5

2^{0,05}

a^6

a^5

Ülesanne 564. Reaalarvulise astendajaga aste

\sqrt[4]{81} =

\sqrt[12]{6} =

\sqrt[3]{0,02} =

\sqrt[25]{10,08} =

8^{\frac{2}{3}} =

80^{\frac{7}{5}} =

0,9^{-\frac{4}{7}} =

7070^{-\frac{8}{9}} =

\sqrt[3]{8^4} =

\sqrt[6]{2,1^3} =

\sqrt[5]{99^{-2}} =

\sqrt[4]{0,052^6} =

Ülesanne 565. Eksponentvõrrandi lahendamine

\left(x+5\right)^{12}=5^{12}
x = või x =

x^{10}=1024
x = või x =

\left(2x-1\right)^9=3^9
x =

x^{11}=2^{11}
x =

\left(x+2\right)^x=5^x
x = või x =

\left(x+7\right)^x=5^x
x = , x = või x =

\left(x^2+2\right)^x=3^x
x₁ = , x₂ = , x₃ =

x^{x+5}=1
x₁ = , x₂ = , x₃ =

x^{\sqrt{x}}=\left(\sqrt{x}\right)^x
x₁ = , x₂ =

x^x=x
x₁ = , x₂ =

x^{1-x}=x^{-1}
x₁ = , x₂ =

x^{x-3}=x^2
x₁ = , x₂ = , x₃ =

Еще на эту тему

Количество баллов Opiq

	Работы
	Параграф проработан

Reaal­arvulise astendajaga aste

Еще на эту тему

Ülesanded A

Ülesanne 543. Reaal­arvulise astendajaga aste

Ülesanne 544. Astendamine

Ülesanne 545. Astendamine

Ülesanne 546. Astendamine

Ülesanne 547. Tehted astmetega

Ülesanne 548. Lihtsustamine

Ülesanne 549. Tehted astmete ja juurtega

Ülesanne 550. Lihtsustamine

Ülesanne 551. Lihtsustamine

Ülesanne 552. Eksponent­võrrandi lahendamine

Ülesanne 553. Reaal­arvulise astendajaga aste

Ülesanne 554. Reaal­arvulise astendajaga aste

Ülesanne 555. Reaal­arvulise astendajaga aste

Ülesanne 556. Reaal­arvulise astendajaga aste

Еще на эту тему

Ülesanded B

Ülesanne 557. Lihtsustamine

Ülesanne 558. Tehted astmete ja juurtega

Ülesanne 559. Võrdlemine

Ülesanne 560. Võrdlemine

Ülesanne 561. Eksponent­võrratuse lahendamine

Ülesanne 562. Võrdlemine

Ülesanne 563. Reaal­arvulise astendajaga aste

Ülesanne 564. Reaal­arvulise astendajaga aste

Ülesanne 565. Eksponent­võrrandi lahendamine

Еще на эту тему

Добавить материал

Загружаемые файлы

Сообщить об ошибке

Сюда пишите только об ошибках Opiq. Пожалуйста, опишите ошибку как можно детальнее.

Если вы согласны поделиться информацией о себе, сообщите свои контактные данные (e-mail, телефон).

Поставьте галочку, чтобы помочь нам бороться со спамом

Opiq использует файлы cookie

Reaalarvulise astendajaga aste

Ülesanne 543. Reaalarvulise astendajaga aste

Ülesanne 552. Eksponentvõrrandi lahendamine

Ülesanne 553. Reaalarvulise astendajaga aste

Ülesanne 554. Reaalarvulise astendajaga aste

Ülesanne 555. Reaalarvulise astendajaga aste

Ülesanne 556. Reaalarvulise astendajaga aste

Ülesanne 561. Eksponentvõrratuse lahendamine

Ülesanne 563. Reaalarvulise astendajaga aste

Ülesanne 564. Reaalarvulise astendajaga aste

Ülesanne 565. Eksponentvõrrandi lahendamine