Квадрат двучлена

(x + y)2 = (x + y)(x + y) =  = 

(m + n)2 = (m + n)(m + n) =  = 

(s + t)2 = (s + t)(s + t) =  = 

(2x + y)2 = (2x + y)(2x + y) =  = 

(a + 3b)2 = (a + 3b)(a + 3b) =  = 

Какую особенность ты подметил в полученных многочленах после приведения в них подобных? Попробуй сформулировать найденную закономерность.

Обозначим один одночлен буквой a, а другой – буквой b. Тогда рас­смотренные выше примеры позволяют записать полученную закономерность в виде облегчающей преобразования формулы квадрата суммы:

(a + b)2 = a2 + 2ab + b2

Квадрат суммы двух одночленов равен квадрату первого члена, плюс удвоенное произведение первого члена на второй, плюс квадрат второго члена.
  1. (3x + 2y)2 = (3x)2 + 2 · 3x · 2y + (2y)2 = 9x2 + 12xy + 4y2
  2. (a2 + 2)2 = (a2)2 + 2 · a2 · 2 + 22 = a4 + 4a2 + 4

(x + m)2 = 

(x + y)2 = 

(u + v)2 = 

(a + x)2 = 

(m + 2)2 = 

(3 + t)2 = 

(x + 10)2 = 

(7 + b)2 = 

(1 + s)2 = 

(2x + 1)2 = 

(2a + b)2 = 

(x + 3y)2 = 

Рассуждая аналогично, легко убедиться (сделай это самостоятельно) в том, что верна и следующая формула:

(a – b)2 = a2 – 2ab + b2,

называемая формулой квадрата разности.

Квадрат разности двух одночленов равен квадрату первого члена, минус удвоенное произведение первого члена на второй, плюс квадрат второго члена.
  1. (3x – 2y)2 = (3x)2 – 2 · 3x · 2y + (2y)2 = 9x2 – 12xy + 4y2
  2. (a – b2)2 = a2 – 2ab2 + (b2)2 = a2 – 2ab2 + b4

(x – y)2 = 

(m – n)2 = 

(s – t)2 = 

(x – a)2 = 

(m – 2)2 = 

(t – 3)2 = 

(x – 5)2 = 

(2 – v)2 = 

(1 – m)2 = 

(2a – 1)2 = 

(3c – d)2 = 

(x – 4y)2 = 

Seotud sisu
Muud tegevused

Упражнения A

201. Квадрат двучлена

Прочитай внимательно текст параграфа и изучи примеры. Сформулируй по памяти, как читаются формулы квадрата суммы и квадрата разности.

(☐ ± △)2 = (☐)2 ± 2 · ☐ · △ + (△)2

(2a + 5)2 = 

(2x – 1)2 = 

(3c + 1)2 = 

(4x + 3)2 = 

(m – 2n)2 = 

(3u – 2)2 = 

(4a – b)2 = 

(2 + 5z)2 = 

(6b – a)2 = 

(8 + 2a)2 = 

(10m + 3n)2 = 

(6a – 8c)2 = 

(5x – 4y)2 = 

(9u + 2v)2 = 

(7y – 3z)2 = 

(ab + c)2 = 

(xy – 4)2 = 

(10 – az)2 = 

(2uv + 3t)2 = 

(4c – 5ab)2 = 

(8a + 0,4b)2 = 

(1,2x – y)2 = 

(2,5u + 4z)2 = 

4a+12b2 = 

6x-13y2 = 

(y2 – 1)2 = 

(a2 + b2)2 = 

(y3 – 3)2 = 

8y-14z2 = 

10z+15u2 = 

204. Обманчивое сходство выражений

Постарайся хорошо уяснить и запомнить, в чем состоит отличие между похожими, но имеющими совершенно разное значение выражениями:

(x + y)2 – квадрат суммы чисел x и y;

x2 + y2 – сумма квадратов чисел x и y;

(x – y)2 – квадрат разности чисел x и y;

x2 – y2 – разность квадратов чисел x и y.

  1. Сумма квадратов чисел 9 и 5.
  2. Квадрат разности чисел 12 и 4.
  3. Разность квадратов чисел 7 и 3.
  4. Квадрат суммы чисел 10 и 15.
  5. Разность квадратов чисел u и v.
  6. Квадрат разности чисел s и t.
  7. Сумма квадратов чисел m и n.
  8. Квадрат суммы чисел x и y.

(4 – 2)2 = 

42 – 22 = 

(4 – 2)2    42 – 22

(3 + 6)2 = 

32 + 62 = 

(3 + 6)2    32 + 62

(5 + 2)2 = 

52 + 22 = 

(5 + 2)2    52 + 22

(9 – 7)2 = 

92 – 72 = 

(9 – 7)2    92 – 72

(12 – 8)2 = 

122 – 82 = 

(12 – 8)2    122 – 82

(1 + 4)2 = 

12 + 42 = 

(1 + 4)2    12 + 42

(a + b)2 ≠ a2 + b2, если a ≠ 0 или b ≠ 0.

Квадрат суммы ≠ сумме квадратов.

(a – b)2 ≠ a2 – b2, если a ≠ 0 или b ≠ 0.

Квадрат разности ≠ разности квадратов.

Примеры.

  1. 622 = (60 + 2)2 = 3600 + 240 + 4 = 3844
  2. 2,92 = (3 – 0,1)2 = 9 – 0,6 + 0,01 = 8,41

412 = 

222 = 

1012 = 

812 = 

132 = 

992 = 

Примеры.

  1. 622 = (60 + 2)2 = 3600 + 240 + 4 = 3844
  2. 2,92 = (3 – 0,1)2 = 9 – 0,6 + 0,01 = 8,41

4,52 = 

3,12 = 

6,52 = 

10,22 = 

4,22 = 

8,12 = 

Примеры.

  1. 622 = (60 + 2)2 = 3600 + 240 + 4 = 3844
  2. 2,92 = (3 – 0,1)2 = 9 – 0,6 + 0,01 = 8,41

192 = 

382 = 

882 = 

292 = 

492 = 

2012 = 

Примеры.

  1. 622 = (60 + 2)2 = 3600 + 240 + 4 = 3844
  2. 2,92 = (3 – 0,1)2 = 9 – 0,6 + 0,01 = 8,41

1,82 = 

5,82 = 

7,82 = 

4,92 = 

9,92 = 

3,92 = 

(a + b)2 – (a – b)2 =  = 

(2x – 5)2 – (x – 5)2 =  = 

(4 – 2p)2 – (2p + 3)2 =  = 

3(y – 2)2 + (y + 3)2 =  = 

(m – n)(m + n) – (m + n)2 =  = 

(c – d)2 + (c + d)(c – d) =  = 

(3c + 1)2 + (c – 1)(c + 1) =  = 

(2u – 1)2 – 4(u + 2)2 =  = 

(x – 3)2 – 2x(x – 9) =  = 

(2a + 3)2 – (a + 2)(a – 1) =  = 

(2m + 1)(m – 1) + (m2 + 1)2 =  = 

(z + 2)(z – 1) – z(z2 – z + 3) =  = 

(2x – 3)(x + 2) – (x – 2)2 – x2 = 

2y(y – 2) + (y + 3)2 – (y + 1)2 = 

(4x – 5y)2 – (2x – 3y)(8x + y) = 

c(c – 2b +1) + (c + b)2 – c(c + 1) = 

(4x – 1)(4x + 1) – (3x – 2)2 + (x + 3)2 = 

2(x – 2)2 – 2x(x – 4) = 

(a – b)2 – b(2a + b) =  = 

Если a = 0,5 и b = –1, то значение выражения равно

 = 

(2x – y)2 + 2x(2y – x) =  = 

Если x = –2 и y = –3, то значение выражения равно

 = 

3u – (u2 + 9v2) + (u – 3v)2 =  = 

Если u=-13 и v=12, то значение выражения равно

 = 

u2 – (u – 2)2 = 20
u = 

(x + 3)2 – x(x – 1) = –12
x = 

(y – 4)(y + 4) – (y – 5)2 = 9
y = 

(t – 1)2 + 12 = (t + 1)2
t = 

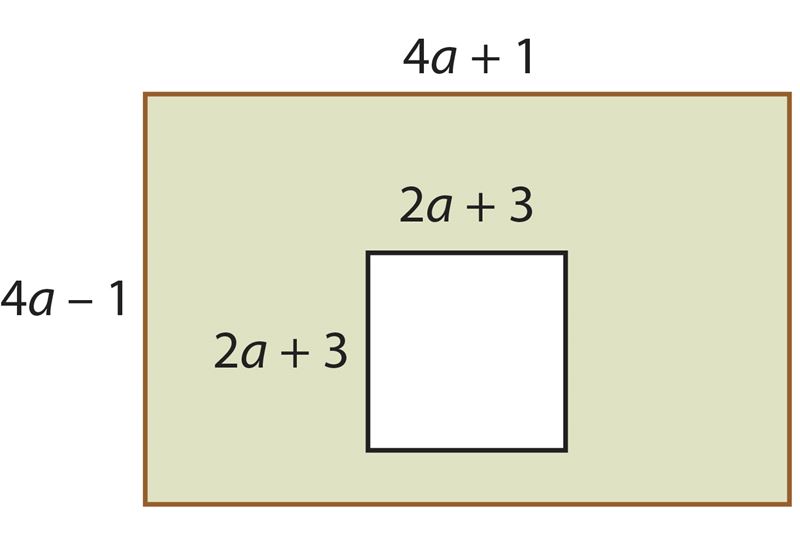
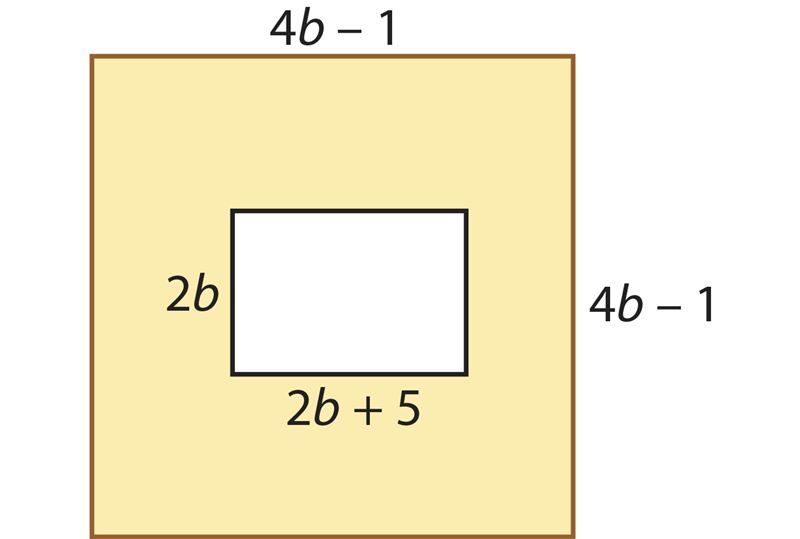
Ответ:  сторона первого квадрата равна  см, а сторона второго –  см.

Ответ: эти числа есть   и .

Seotud sisu
Muud tegevused

Упражнения Б

(y3 – 3y2)2 = 

(2x2 + 5y2)2 = 

(m2 – m4)2 = 

a32+b252 = 

s4-s232 = 

(a2b3 + a)2 = 

(0,2z2 – x3y)2 = 

(15ac3 + 0,6c)2 = 

12x3y-4y22 = 

213u+6u42 = 

(mn + 2)2 = 

(xa – yb)2 = 

(am+1 – am)2 = 

(y2n + 1)2 = 

(d2m–2 + d2)2 = 

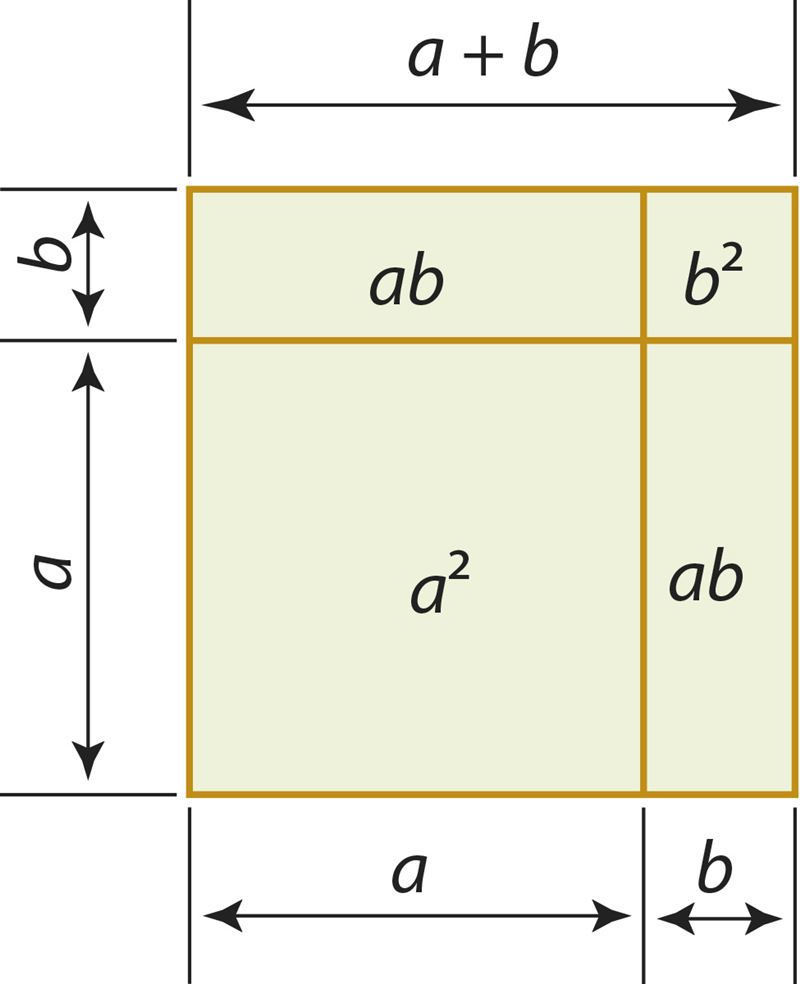
216. Практическая работа

  1. Вырежи из бумаги квадрат со стороной a. 
  2. Вырежи из бумаги также два прямоугольника с измерениями a и b (b < a) .
  3. Расположи прямоугольники на квадрате и обоснуй с помощью площадей фигур справедливость формулы a2 – 2ab + b2 = (a – b)2.

(x – y)2 = (y – x)2

(–a – b)2 = (a + b)2

(a – b)(b – a) = –(a – b)2

(x + y)2 – (x – y)2 = 4xy

2(c – d)2 – 4(c + d)(c – d) + 2(c + d)2 = 

(a2 – 2b)2 + (a2 – 2b)(a2 + 2b) – (a2 + 2b) · a2 = 

(2a3 – b2)2 – (2a4 – b2)(2a2 – b2) + 2a3b2(2 – a) = 

–(2x + 5y)(2x – 5y) – 6(2y – 5x)2 – 3(5x + 2y)2 = 

(m – 2n)2 – m(m – 8n) =  = 

Если m = 9,9 и n = 0,1, то значение выражения равно

 = 

(3x – y)2 – (3x – y)(3x + y) =  = 

Если x = –0,15 и y = 0,85, то значение выражения равно

 = 

Используй полученный результат при устных вычислениях, например:

652 = 100 · 6 · 7 + 25 = 4225.

(4x + 2)2 – (4x – 3)2 – 20(x + 3) = 5
x = 

(x – 5)2 + (x – 2)(x + 3) = 2(x2 – 3) – 11
x = 

3(y – 1)2 + (2y + 3)2 – 7(y – 1)(y + 1) = 1
y = 

2(t + 3)2 – (t – 4)(t + 2) = t(t + 2) – 22
t = 

S =  = 

S =  = 

Ответ: сторона первоначального квадрата равна   см.

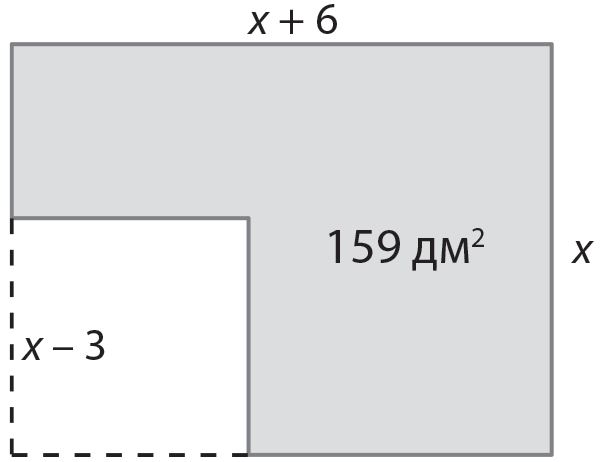
Ответ: первоначально измерения листа жести были   дм и  дм.

Подсказка
Общий вид нечетного числа 2n + 1 или 2n – 1.

Seotud sisu
Muud tegevused