Siinus­funktsioon

Esma­kordselt selgitasime juba X klassis, et igale nurgale vastab üks siinuse väärtus. Eelmises pea­tükis näitasime, et igale reaal­arvule x saab vastavusse seada siinuse väärtuse sin x. Tähistame viimase tähega y ja vaatame suurust x muutujana. Siis võrdus y = sin x seab reaal­arvule x vastavusse reaal­arvu y, s.t defineerib funktsiooni, mida nimetatakse siinus­funktsiooniks.

Eel­öeldust järeldub, et siinus­funktsiooni y = sin x määramis­piirkonnaks on kogu reaal­arvude hulk R, muutumis­piirkonnaks aga lõik [–1; 1], s.t –1 ≤ sin x ≤ 1 ehk |sin x| ≤ 1.

Seosest sin(–x) = –sin x järeldub, et

siinus­funktsioon on paaritu funktsioon.

Järelikult,

siinus­funktsiooni graafik on sümmeetriline koordinaatide algus­punkti suhtes.

Seega võime y = sin x graafiku konstrueerida esi­algu vaid argumendi positiivsete väärtuste korral ja siis, sümmeetriale tuginedes, kogu määramis­piirkonna ulatuses.

Seosest sin(x + n · 2π) = sin x, kus n ∈ Z, järeldub, et sin x väärtused korduvad iga 2π järel. Siis võib aga funktsiooni y = sin x graafiku konstrueerida mingil lõigul pikkusega 2π, näiteks lõigul [0; 2π], ja see­järel jätkata samal viisil nii suures ulatuses kui vaja.

Et siinus­funktsiooni väärtused korduvad iga 2π järel, siis öeldakse, et

siinus­funktsioon on perioodiline funktsioon perioodiga 2π.

Kõige lihtsam on konstrueerida siinus­funktsiooni graafikut, sinusoidi (joonis 3.19), aga laua­arvuti abil, kasutades selleks näiteks programmi GeoGebra.

Joon. 3.19

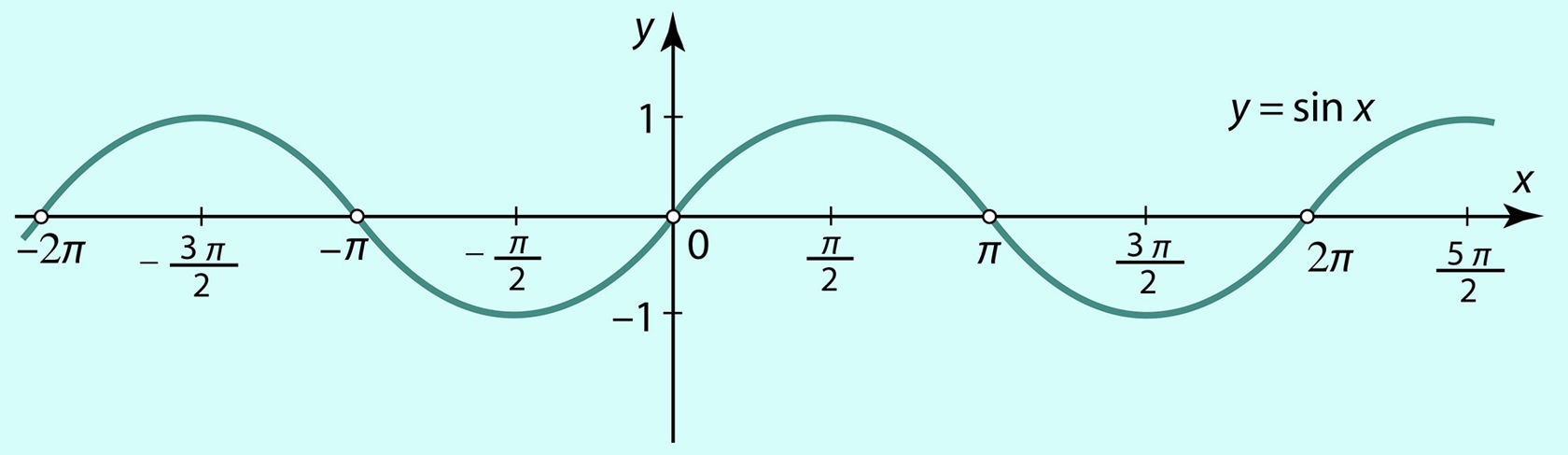
Et sinusoid on pidev joon, siis võib ka öelda, et funktsioon y = sin x on pidev.

Graafikult on võimalik välja lugeda mitmeid siinus­funktsiooni omadusi.

  1. Siinus­funktsiooni null­kohtadeks on argumendi väärtused
    ​…, –2π, –π, 0, π, 2π, 3π, … ehk nπ, kus n ∈ Z.
  2. Siinus­funktsiooni positiivsus­piirkonna moodustavad vahemikud
    ​…, –2π < x < –π, 0 < x < π, 2π < x < 3π, …,
    ​mis korduvad iga 2π järel, s.o vahemikud 2nπ < x < π + 2nπ, kus n ∈ Z.
  3. Siinus­funktsiooni negatiivsus­piirkonna moodustavad vahemikud
    ​…, –π < x < 0, π < x < 2π, …,
    ​mis korduvad samuti iga 2π järel, s.o vahemikud –π + 2nπ < x < 2nπ, kus n ∈ Z.
  4. Funktsiooni y = sin x kasvamis­vahemikud on
    ​…, -\frac{5\pi}{2}<x<\frac{3\pi}{2}, -\frac{\pi}{2}<x<\frac{\pi}{2}, \frac{3\pi}{2}<x<\frac{5\pi}{2}, …
    ​ehk -\frac{\pi}{2}+2n\pi<x<\frac{\pi}{2}+2n\pi, n ∈ Z.
  5. ning kahanemis­vahemikud on
    ​…, -\frac{3\pi}{2}<x<-\frac{\pi}{2}, \frac{\pi}{2}<x<\frac{3\pi}{2}, …
    ​ehk \frac{\pi}{2}+2n\pi<x<\frac{3\pi}{2}+2n\pi, n ∈ Z.
  6. Funktsiooni y = sin x miinimum­kohad on
    ​…, -\frac{5\pi}{2}, -\frac{\pi}{2}, \frac{3\pi}{2}, \frac{7\pi}{2}, …
    ​ehk \frac{3\pi}{2}+2n\pi, kus n ∈ Z.
  7. ja maksimum­kohad on
    ​…, -\frac{3\pi}{2}, \frac{\pi}{2}, \frac{5\pi}{2}, ...
    ​ehk \frac{\pi}{2}+2n\pi, kus n ∈ Z.

Näide 1.

Kasutades siinus­funktsiooni graafikut, leiame, 1) millise märgiga on sin 3,5 väärtus ja 2) kumb on suurem, kas sin 2 või sin 3.

  1. Et π < 3,5 < 2π, s.t 3,5 kuulub funktsiooni y = sin x negatiivsus­piirkonda (vt joon. 3.19), siis on sin 3,5 väärtus negatiivne.
  2. Et \frac{\pi}{2}<2<3<\pi, s.t argumendi väärtused kuuluvad siinus­funktsiooni kahanemis­vahemikku (vt joon. 3.19), siis sin 2 > sin 3.

Näide 2.

Lahendame võrrandi \sin x=-\frac{\sqrt{3}}{2}.

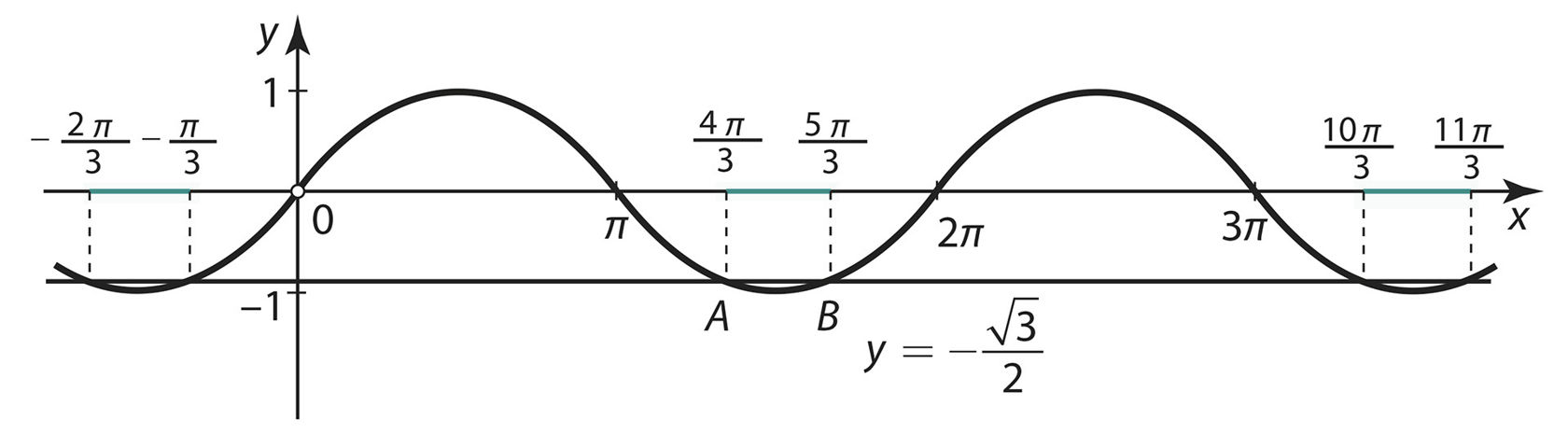
Joonestame siinus­funktsiooni graafiku ja sirge y=-\frac{\sqrt{3}}{2} (joonis 3.20). Võrrandi lahendeiks on nende joonte lõike­punktide abstsissid. Et \sin\frac{\pi}{3}=\frac{\sqrt{3}}{2}, siis punktide A ja B abstsissid on vastavalt \pi+\frac{\pi}{3}=\frac{4\pi}{3} ja 2\pi-\frac{\pi}{3}=\frac{5\pi}{3}, mille korral \sin\left(\pi+\frac{\pi}{3}\right)=-\sin\frac{\pi}{3}=-\frac{\sqrt{3}}{2} ning \sin\left(2\pi-\frac{\pi}{3}\right)=-\sin\frac{\pi}{3}=-\frac{\sqrt{3}}{2}.

Joon. 3.20

Meid huvitavad lõike­punktid korduvad iga 2π järel. Seega on võrrandi \sin x=-\frac{\sqrt{3}}{2} lahendid x_1=\frac{4\pi}{3}+n\cdot2\pi ja x_2=\frac{5\pi}{3}+n\cdot2\pi, kus n ∈ Z; näiteks -\frac{2\pi}{3} ja -\frac{\pi}{3}, kui n = –1, \frac{10\pi}{3} ja \frac{11\pi}{3}, kui n = 1.

Näide 3.

Konstrueerime funktsiooni y = 2 – sin x graafiku piir­konnas [–π; 2π] ja uurime selle abil antud funktsiooni.

Vaadeldava funktsiooni graafiku võiksime konstrueerida arvuti abil, kasutades näiteks programmi GeoGebra.

Mõnusat jõu­kohast arutlust pakub aga graafiku konstrueerimine varem õpitud arvuliste suuruste, näiteks kordajate mõju arvestamise teel graafikute juures. Seega konstrueerime esmalt funktsiooni y = sin x graafiku (joonis 3.21), siis sellest lähtudes y = –sin x graafiku ja see­järel viimasest lähtudes y = 2 – sin x graafiku. Võrreldes funktsiooni y = –sin x funktsiooniga y = sin x näeme, et muutuja y kõik väärtused on vastu­pidise märgiga võrreldes funktsiooniga y = sin x, mis graafikute seisu­kohalt tähendab vastavate graafikute sümmeetrilisust x-telje suhtes. Teisiti öeldes saadakse y = –sin x graafik y = sin x graafikust viimase peegeldamisel x-teljest. Funktsiooni y = 2 – sin x ehk y = –sin x + 2 graafiku saame aga y = –sin x graafikust selle nihutamisel 2 ühiku võrra üles­poole.

Joon. 3.21

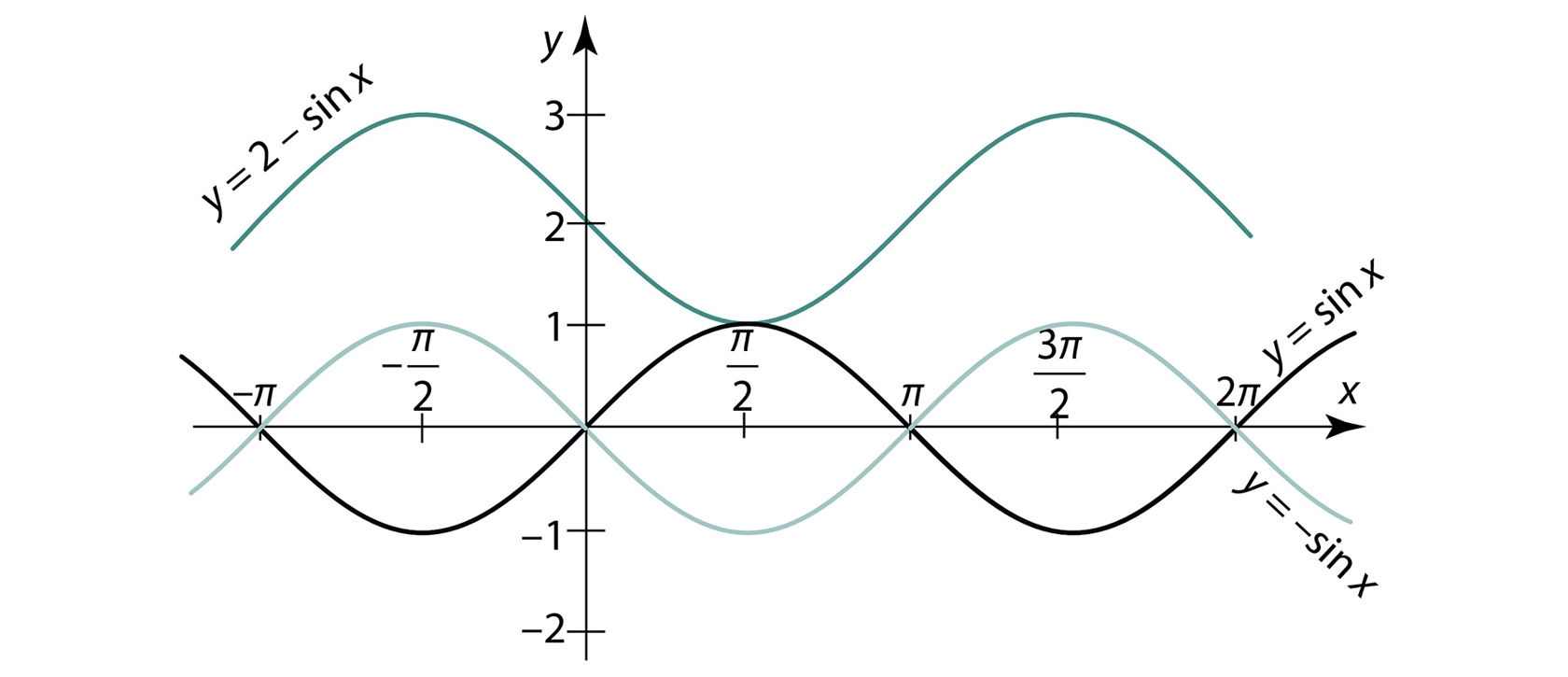
Funktsiooni y = 2 – sin x määramis­piirkond X = [–π; 2π], null­kohad puuduvad (graafik ei lõika x-telge), positiivsus­piirkond X+ = [–π; 2π], negatiivsus­piirkond puudub, s.t X– = ∅, kasvamis­vahemikud on X_1\uparrow=\left[-\pi;\ -\frac{\pi}{2}\right) ja X_2\uparrow=\left(\frac{\pi}{2};\ \frac{3\pi}{2}\right), kahanemis­vahemikud on X_1\downarrow=\left(-\frac{\pi}{2};\ \frac{\pi}{2}\right) ja X_2\downarrow=\left(\frac{3\pi}{2};\ 2\pi\right].

Näide 4.

Lahendame võrratuse \sin x<-\frac{\sqrt{3}}{2}.

Kasutame jälle joonist 3.20, kus on nii siinus­funktsiooni graafik kui ka sirge y=-\frac{\sqrt{3}}{2}. Et \sin x<-\frac{\sqrt{3}}{2}, siis järelikult otsime x-teljelt piir­konda, kus funktsiooni y = sin x graafik on all­pool sirget y=-\frac{\sqrt{3}}{2}. Üheks selliseks vahemikuks on \frac{4\pi}{3}<x<\frac{5\pi}{3}. Punktide A ja B abstsissid leidsime näites 2. Kuna vastavad piir­konnad korduvad iga 2π järel, siis võrratuse \sin x<-\frac{\sqrt{3}}{2} lahend koosneb vahemikest

…, -\frac{2\pi}{3}<x<\frac{\pi}{3}, \frac{4\pi}{3}<x<\frac{5\pi}{3}, \frac{10\pi}{3}<x<\frac{11\pi}{3}, …

ehk lühemalt, vahemikest

\frac{4\pi}{3}+2n\pi<x<\frac{5\pi}{3}+2n\pi, n ∈ Z.

More like this
More options

Ülesanded A

Ülesanne 689. Funktsiooni y = sin x väärtused

x väärtus

x=\frac{\pi}{4}

x=\frac{\pi}{3}

x=-\frac{\pi}{2}

x=\frac{4\pi}{27}

Funktsiooni väärtus

x väärtus

x=\frac{8\pi}{45}

x=-\frac{5\pi}{16}

x=2,25

x=-0,07

Funktsiooni väärtus

Ülesanne 690. Võrrandi lahendamine

Vastus. x = , kus n ∈ Z.

Ülesanne 691. Avaldise märgi leidmine

Avaldis

Avaldise märk

\sin5

\sin\left(-3\right)

\sin\left(-1\right)

\sin7

Avaldis

Avaldise märk

\sin\frac{3\pi}{8}

\sin\left(-\frac{3\pi}{2}\right)

\sin\left(-\frac{7\pi}{10}\right)

\sin\frac{7\pi}{10}

Ülesanne 692. Võrdlemine

\sin4,2  \sin1,8

\sin\left(-4,5\right)  \sin\left(-3,8\right)

\sin\frac{3\pi}{4}  \sin\frac{4\pi}{3}

\sin2\pi  \sin\frac{7\pi}{4}

Ülesanne 693. Funktsiooni maksimum ja miinimum

y = 3 + 4sin x

Vastus. Sellel funktsioonil on maksimum, kui x = , n ∈ Z ja miinimum, kui x = , n ∈ Z. y_{\max} =  ja y_{\min} = .

y = 2 – sin x

Vastus. Sellel funktsioonil on maksimum, kui x = , n ∈ Z ja miinimum, kui x = , n ∈ Z. y_{\max} =  ja y_{\min} = .

y = 0,75 sin x

Vastus. Sellel funktsioonil on maksimum, kui x = , n ∈ Z ja miinimum, kui x = , n ∈ Z. y_{\max} =  ja y_{\min} = .

y = sin2 x

Vastus. Sellel funktsioonil on maksimum, kui x = , n ∈ Z ja miinimum, kui x = , n ∈ Z. y_{\max} =  ja y_{\min} = .

Ülesanne 694. Vaate­ratas
Joon. 3.22

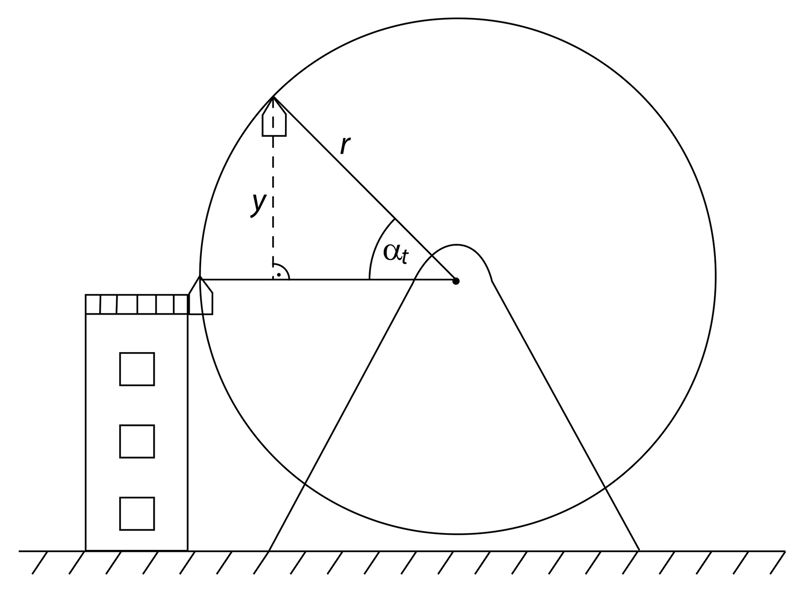
Vastus. Kui nurk on antud radiaanides, siis on otsitav funktsioon y = . Kui nurk on antud kraadides, siis on otsitav funktsioon y = . See on funktsioon.

  • Kirjutage välja konkreetne funktsioon, kui r = 8 m ja t0 = 10 minutit.
    Vastus. y =  (radiaanides), y =  (kraadides).
  • Konstrueerige selle funktsiooni graafik piir­konnas 0 ≤ t ≤ 10.
  • Milliste t väärtuste korral kabiin
    1. on kõrgemal platvormist,
      Vastus. Kabiin on kõrgemal platvormist, kui t ∈ .
    2. langeb?
      Vastus. Kabiin langeb, kui t ∈ .
Ülesanne 695. Funktsiooni graafiku konstrueerimine

695.1 Funktsiooni graafiku konstrueerimine

Konstrueerige funktsiooni graafik antud piir­konnas arvuti abil (näiteks programm GeoGebra) üksikute punktide kaupa või õpiku näite 3 ees­kujul.

y=2\sin x,\ -\pi\le x\le2\pi

695.2 Funktsiooni graafiku konstrueerimine

Konstrueerige funktsiooni graafik antud piir­konnas arvuti abil (näiteks programm GeoGebra) üksikute punktide kaupa või õpiku näite 3 ees­kujul.

y=0,5\sin x, -\pi\le x\le2\pi

695.3 Funktsiooni graafiku konstrueerimine

Konstrueerige funktsiooni graafik antud piir­konnas arvuti abil (näiteks programm GeoGebra) üksikute punktide kaupa või õpiku näite 3 ees­kujul.

y=1+\sin x, 0\le x\le3\pi

695.4 Funktsiooni graafiku konstrueerimine

Konstrueerige funktsiooni graafik antud piir­konnas arvuti abil (näiteks programm GeoGebra) üksikute punktide kaupa või õpiku näite 3 ees­kujul.

y=\sin x-2, 0\le x\le2\pi

695.5 Funktsiooni graafiku konstrueerimine

Konstrueerige funktsiooni graafik antud piir­konnas arvuti abil (näiteks programm GeoGebra) üksikute punktide kaupa või õpiku näite 3 ees­kujul.

y=-\sin x, 0\le x\le4\pi

695.6 Funktsiooni graafiku konstrueerimine

Konstrueerige funktsiooni graafik antud piir­konnas arvuti abil (näiteks programm GeoGebra) üksikute punktide kaupa või õpiku näite 3 ees­kujul.

y=2-\sin x, 0\le x\le4\pi

Ülesanne 696. Funktsiooni null­kohad

y=2\sin x, -\pi\le x\le2\pi

Vastus. X_0 = 

y=0,5\sin x, -\pi\le x\le2\pi

Vastus. X_0 = 

y=1+\sin x, 0\le x\le3\pi

Vastus. X_0 = 

y=\sin x-2, 0\le x\le2\pi

Vastus. X_0 = 

y=-\sin x, 0\le x\le4\pi

Vastus. X_0 = 

y=2-\sin x, 0\le x\le4\pi

Vastus. X_0 = 

Ülesanne 697. Funktsiooni positiivsus- ja negatiivsus­piirkonnad

y=2\sin x, -\pi\le x\le2\pi

Vastus. X^+ = , X^- = 

y=0,5\sin x, -\pi\le x\le2\pi

Vastus. X^+ = , X^- = 

y=1+\sin x, 0\le x\le3\pi

Vastus. X^+ = , X^- = 

y=\sin x-2, 0\le x\le2\pi

Vastus. X^+ = , X^- = 

y=-\sin x, 0\le x\le4\pi

Vastus. X^+ = , X^- = 

y=2-\sin x, 0\le x\le4\pi

Vastus. X^+ = , X^- = 

Ülesanne 698. Funktsiooni kasvamis- ja kahanemis­vahemikud ning maksimum ja miinimum

y=2\sin x, -\pi\le x\le2\pi

Vastus. X_1\uparrow = , X_2\uparrow = , X_1\downarrow = , X_2\downarrow = , y_{\max} = , y_{\min} = .

y=0,5\sin x, -\pi\le x\le2\pi

Vastus. X_1\uparrow = , X_2\uparrow = , X_1\downarrow = , X_2\downarrow = , y_{\max} = , y_{\min} = .

y=1+\sin x, 0\le x\le3\pi

Vastus. X_1\uparrow = , X_2\uparrow = , X_1\downarrow = , X_2\downarrow = , y_{\max} = , y_{\min} = .

y=\sin x-2, 0\le x\le2\pi

Vastus. X_1\uparrow = , X_2\uparrow = , X\downarrow = , y_{\max} = , y_{\min} = .

y=-\sin x, 0\le x\le4\pi

Vastus. X_1\uparrow = , X_2\uparrow = , X_1\downarrow = , X_2\downarrow = , X_3\downarrow = , y_{\max} = , y_{\min} = .

y=2-\sin x, 0\le x\le4\pi

Vastus. X_1\uparrow = , X_2\uparrow = , X_1\downarrow = , X_2\downarrow = , X_3\downarrow = , y_{\max} = , y_{\min} = .

Ülesanne 699. Võrrandi lahendamine

\sin x=\frac{1}{2}

Vastus. ..., , , , ... ja ..., , , , ... ehk x1 =  ja x2 = , n ∈ Z.

\sin x=1

Vastus. ..., , , , ... ehk x = , n ∈ Z.

\sin x=-\frac{\sqrt{2}}{2}

Vastus. ..., , , , ... ja ..., , , , ... ehk x1 =  ja x2 = , n ∈ Z.

More like this
More options

Ülesanded B

Ülesanne 700. Funktsiooni graafiku konstrueerimine

y=2+2\sin x, 0\le x\le3\pi

Vastus. X_0 = ; X^+ = ; X^- = ; X_1\uparrow = ; X_2\uparrow = ; X_1\downarrow = ; X_2\downarrow = 

y=-1+2\sin x, 0\le x\le3\pi

Vastus. X_0 = ; X^+ = ; X^- = ; X_1\uparrow = ; X_2\uparrow = ; X_1\downarrow = ; X_2\downarrow = 

y=\left|\sin x\right|, -2\pi\le x\le3\pi

Vastus. X_0 = ; X^+ = ; X^- = ; X_1\uparrow = ; X_2\uparrow = ; X_3\uparrow = ; X_4\uparrow = ; X_5\uparrow = ; X_1\downarrow = ; X_2\downarrow = ; X_3\downarrow = ; X_4\downarrow = ; X_5\downarrow = 

y=\left|\sin x\right|-1, -2\pi\le x\le3\pi

Vastus. X_0 = ; X^+ = ; X^- = ; X_1\uparrow = ; X_2\uparrow = ; X_3\uparrow = ; X_4\uparrow = ; X_5\uparrow = ; X_1\downarrow = ; X_2\downarrow = ; X_3\downarrow = ; X_4\downarrow = ; X_5\downarrow = 

Ülesanne 701. Võrrandi lahendamine

\sin x=\frac{\sqrt{3}}{2}

Vastus. ..., , , , ... ja
..., , , , ...
ehk x1 =  ja x2 = , n ∈ Z.

\sin x=-\frac{1}{2}

Vastus. ..., , , , ... ja
..., , , , ...
ehk x1 =  ja x2 = , n ∈ Z.

\sin x=0,66

Vastus. ..., , , , ... ja
..., , , , ...
ehk x1 =  ja x2 = , n ∈ Z.

\sin x=0

Vastus. ..., , , , ...
ehk x = , n ∈ Z.

Ülesanne 702. Võrratuse lahendamine

\sin x>0,5

Vastus.  < x < , n ∈ Z.

\sin x<0,5

Vastus.  < x < , n ∈ Z.

\sin x>-0,5

Vastus.  < x < , n ∈ Z.

\sin x\ge-1

Vastus. x ∈ 

\sin x>\frac{\sqrt{3}}{2}

Vastus.  < x < , n ∈ Z.

\sin x<-\frac{\sqrt{2}}{2}

Vastus.  < x < , n ∈ Z.

\sin x>0,12

Vastus.  < x < , n ∈ Z.

\sin x<0,66

Vastus.  < x < , n ∈ Z.

More like this
More options