Harilikud murrud

Tunni ülesehitus

  1. Häälestus, 5 min
  2. Harilikud murrud, 20 min
  3. Iseseisev töö, 15 min
  4. Tagasiside, 5 min

Ettevalmistus

Printida väljapääsupiletid ja soovi korral ka vastused.

Eelteadmised

Õpilane

  • tunneb harilikke murde;
  • teab, mida näitab murru lugeja ja nimetaja;
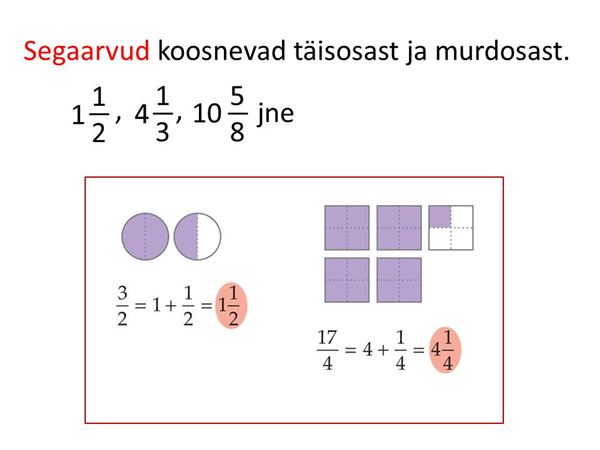
  • teab, et segaarv koosneb täisosast ja murdosast;
  • leiab arvust  1 2 ,  1 3 ,  1 4 ,  1 5  ja  1 6 .

Tunni eesmärgid

Õpilane

  • saab aru, millal tekib harilik murd;
  • teab, et murrujoonel on jagamismärgi tähendus;
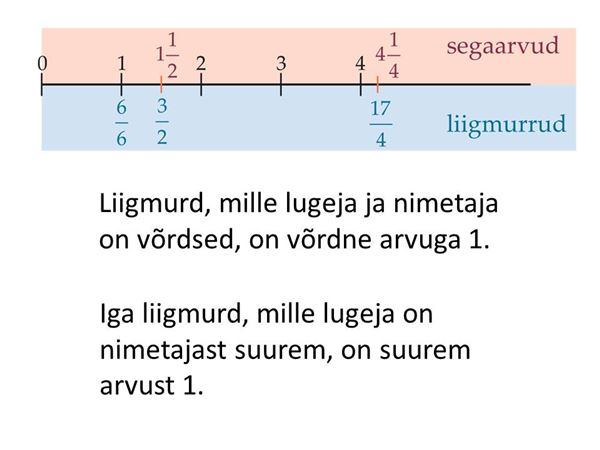
  • liigitab harilikke murde liht­murdudeks, liig­murdudeks ja sega­arvudeks;
  • teab, et lihtmurrud on väiksemad arvust 1;
  • teab, et liigmurrud on suuremad arvust 1 või võrdsed 1-ga.

Seotud õppematerjal

Märksõnad ja meetodid

  • Harilik murd, nimetaja, lugeja, lihtmurd, liigmurd, segaarv, ühiklõik
  • Animatsioonid, arutelu, suuline selgitamine, võimlemis­paus, iseseisev töö, väljapääsupilet

Lõiming

Läbivad teemad

  • Elukestev õpe ja karjääri planeerimine
Seotud sisu
Muud tegevused

Häälestus

5

  • Animatsioon
  • Tänase tunni eesmärgid

Õpetaja näitab häälestuseks animatsiooni sellest, kuidas tekkisid murrud.

Distantsõpe

Õpilased vaatavad ptk 1.2 animat­siooni „Kuidas tekkisid harilikud murrud?“ ja töötavad seejärel läbi teooria osa (kolm järgmist alateemat).

  • Mõelge veel mingi olukorra peale, kus tuleks kasutada murde.
  • Kus asub murru lugeja, kus nimetaja?

Tänases tunnis tuletame meelde, kuidas tekivad harilikud murrud ja kuidas neid liigitatakse. Saame ka teada, mis tähendus on murru­joonel.

Seotud sisu
Muud tegevused

Harilikud murrud

20

  • Animatsioon hariliku murru tekkimisest
  • Arutelu
  • Tekstülesande koostamine
  • Lihtmurrud ja liigmurrud
  • Võimlemispaus
  • Õ lk 10 ül 2 (Opiq ül 1)
  • Selgitamine suuliselt

Õpetaja näitab animatsiooni pitsade jagamisest ja hariliku murru tekkimisest.

Millal tekib harilik murd?

Distantsõpe

Õpilased lahendavad iseseisvalt ül 1a–1c.

Arutelu

Pärast animatsiooni vaatamist arutletakse murdude üle.

  • Mida näitab murru nimetaja?
  • Mida näitab murru lugeja?
  • Kuidas nimetatakse murdu  3 4  teisiti? Kolmveerand
  • Kuidas nimetatakse murdu  1 4 ? Veerand
  • Kuidas saab kellaaega kolmveerand üheksa teisiti öelda? 8.45
    Aga veerand üheksa? 8.15​
  • Millise tehtemärgi tähendus on murru­joonel? Jagamis­märgi 

Ülesande koostamine

Õpetaja kuvab ekraanil kaheksaks võrdseks osaks jaotatud ringi ja palub õpilastel vastata joonise juures olevale küsimusele.

Ring on jaotatud kaheksaks võrdseks osaks. 1= 8 8
Ühe osa suurus on  1 8

Pärast küsimustele vastamist koostavad õpilased joonise kohta tekst­ülesande ning esitavad selle pingi­naab­rile. 

Lihtmurrud ja liigmurrud

Järgmisena tuletatakse meelde, millal on tegemist liht­murruga, liig­murruga ja sega­arvuga.

Iga slaidi juures palub õpetaja tuua õpilastel veel näiteid või vastata küsimusele (vt piltide allkirju).

Too veel näiteid liht- ja liigmurdudest.
Millisest arvust on segaarvud alati suuremad?
Nimeta mõni lihtmurd, mis on väiksem kui  1 3 .
Nimeta mõni liigmurd, mis on võrdne arvuga 1. Nimeta mõni liigmurd, mis on suurem arvust 1.

Liikumispaus

Õpilased tõusevad püsti. Õpetaja hakkab nimetama harilikke murde.

  • Kui see arv on liigmurd, siis tõstavad õpilased käed korraks ülesse ja venitavad ennast hästi pikaks.
  • Kui see arv on lihtmurd, siis puudutavad õpilased korraks kätega põrandat. 
  • Kui see arv on segaarv, siis pööravad õpilased oma ülakeha korraks paremale ja vasakule.

Distantsõpe

Kui õpilased osalevad tunnis reaalajas, siis palub õpetaja ka nendel liikumis­pausist osa võtta.

Õ lk 10 ül 2

Opiq ptk 1.2 ül 1

Õpilased avavad ptk 1.2 või lk 10 ja loevad läbi soovituse. Seejärel kirjutavad nad igale joonisele vastava murru ja valivad murru liigi (vihikus joonivad alla liig­murrud). 

Kiiremad õpilased mõtlevad ise välja analoogseid ülesandeid ja joonestavad need oma vihikusse.

Suuline selgitamine

Ülesande lahendust kontrollitakse suuliselt. Õpetaja kuvab joonise ekraanil. Õpilane ütleb murru, seejärel selgitab, milline arv on lugeja (miks?) ja milline nimetaja (miks?) ning põhjendab, miks murd on liigmurd või lihtmurd.

Kui õpilastele valmistab raskusi lausetega selgitamine, siis võib õpetaja tahvlile lausete algused ette kirjutada.

  1. Joonisel on kujutatud murdu ...
  2. Murru nimetaja on ..., sest ...
  3. Murru lugeja on ..., sest ...
  4. See murd on lihtmurd/liigmurd, sest ...​
Joonisel on kujutatud murdu  1 4 . Murru nimetaja on 4, sest kujund on jagatud neljaks võrdseks osaks. Murru lugeja on 1, sest neljast osast on värvitud üks osa. See on lihtmurd, sest murru lugeja on väiksem kui nimetaja.
Joonisel on kujutatud murdu  2 2 . Murru nimetaja on 2, sest kujund on jagatud kaheks võrdseks osaks. Murru lugeja on 2, sest kahest osast on värvitud kaks osa. See on liigmurd, sest lugeja ja nimetaja on võrdsed.
Joonisel on kujutatud murdu  0 6 . Murru nimetaja on 6, sest kujund on jagatud kuueks võrdseks osaks. Murru lugeja on 0, sest ühtegi osa ei ole värvitud. See on lihtmurd, sest lugeja on väiksem kui nimetaja.
Joonisel on kujutatud murdu  4 8 . Murru nimetaja on 8, sest kujund on jagatud 8-ks võrdseks osaks. Murru lugeja on 4, sest värvitud on neli osa. See on lihtmurd, sest murru lugeja on väiksem kui nimetaja.
Joonisel on kujutatud murdu  6 4 . Murru nimetaja on 4, sest kujundid on jagatud 4-ks võrdseks osaks. Murru lugeja on 6, sest värvitud on kuus osa. See on liigmurd, sest lugeja on suurem kui nimetaja.
Joonisel on kujutatud murdu  5 3 . Murru nimetaja on 3, sest kujundid on jagatud 3-ks võrdseks osaks. Murru lugeja on 5, sest värvitud on viis osa. See on liigmurd, sest lugeja on suurem kui nimetaja.
Joonisel on kujutatud murdu  3 2 . Murru nimetaja on 2, sest kujundid on jagatud kaheks võrdseks osaks. Murru lugeja on 3, sest värvitud on kolm osa. See on liigmurd, sest lugeja on suurem kui nimetaja.
Joonisel on kujutatud murdu  6 4 . Murru nimetaja on 4, sest kujundid on jagatud 4-ks võrdseks osaks. Murru lugeja on 6, sest värvitud on kuus osa. See on liigmurd, sest lugeja on suurem kui nimetaja.
Joonisel on kujutatud murdu  8 3 . Murru nimetaja on 3, sest kujundid on jagatud 3-ks võrdseks osaks. Murru lugeja on 8, sest värvitud on 8 osa. See on liigmurd, sest lugeja on suurem kui nimetaja.
Joonisel on kujutatud murdu  4 1 . Murru nimetaja on 1, sest kujundeid ei ole jagatud väiksemateks osadeks (iga kujund on 1 osa). Murru lugeja on 4, sest värvitud on neli osa. See on liigmurd, sest lugeja on suurem kui nimetaja.
Seotud sisu
Muud tegevused

Iseseisev töö

15

  • TV 1. osa ül 1–11

Õpilased lahendavad iseseisvalt ül 1–11. Soovi korral saab õpetaja saata neile ülesanded ptk 1.2 ülesannete kogust. 

Ülesanded jäävad kodus lõpetada.

Distantsõpe

Õpetaja saadab õpilastele ptk 1.2 ülesannete kogus olevad ülesanded 1–5.

Seotud sisu
Muud tegevused

Tagasiside

5

  • Väljapääsupilet

Õpetaja annab igale õpilasele välja­pääsu­pileti. Kes saab pileti täidetud, annab selle õpetajale ja võib minna vahe­tundi.

Väljapääsupileti vastused

Seotud sisu
Muud tegevused

Kodutöö ja tunni kirjeldus

Kodutöö

Korda harilikke murde, lõpeta TV ül 1–11.

Tunni kirjeldus

Harilikud murrud. Liht- ja liig­murrud, sega­arvud

Opiq ptk 1.2, ​Õ lk 8–9, TV lk 4–5

Seotud sisu
Muud tegevused