Peatükk 1.1 (GLM 1.)

Põhilised tehted hulkadega

  • Hulkadega seotud sümbolid ja tähistused
  • Hulkadega ühendid
  • Hulkade ühisosa
  • Hulkade vahe
Seotud sisu
Muud tegevused

Hulgad

Hulk ja osahulk

Hulk

Hulk on objektide kogum, mida vaadeldakse tervikuna.

Neid objekte nimetatakse hulga elementideks.

Tühi hulk

Hulka, mis ei sisalda ühtegi elementi, nimetatakse tühjaks hulgaks ehk tühihulgaks. 

Osahulk

Kui kõik hulga B elemendid kuuluvad hulka A, siis hulk B on hulga A osahulk.

B ⊂ A või A ⊃ B

Näide 1

Paarisarvude hulk ühest kümneni

A = {2; 4; 6; 8; 10}.

Naturaalarvude hulk

ℕ = {1; 2; 3; ...}.

Viiest väiksemate ja miinus kolmest mitte väiksemate reaalarvude hulk

B = {x| –3 ≤ x < 5}.

Tähistused

Hulkade tähistamiseks kasutatakse suuri tähti. Näiteks

K = {x; y; z}, L = {1; 2; 3}, M = {}.

 x ∈ K,

x ∉ L,

M = ∅.

Märka

Üksiku elemendi hulka kuulumise või mittekuulumise sümbolid on

∈ ja ∉.

Terve hulga kuulumist või mitte­kuulumist teise hulka tähistame märkidega 

⊂, ⊃, ⊄, ⊅.

Mõtle

Kui kehtib lause A ⊂ P,  siis millisel juhul on tõene ka lause P ⊂ A?

Seotud sisu
Muud tegevused

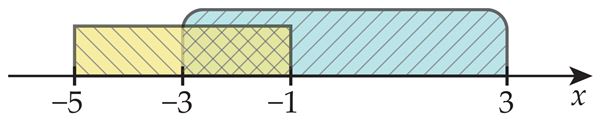
Hulkade ühendamine

Hulkade ühend

Kahe hulga A ja B ühendiks ehk summaks A ∪ B  nimetatakse hulka C, mille moodustavad kõik elemendid, mis kuuluvad hulka A või hulka B.

C = A ∪ B 

Operatsioon või

Olgu x hulga C element, siis x kuulub hulka A või hulka B. Hulgateoorias pannakse see lause kirja nii:

x ∈ A ∪ B ⇔ (x ∈ A) ∨ (x ∈ B).

Loogilist operatsiooni või tähistab sümbol ∨.

Hulkade ühend

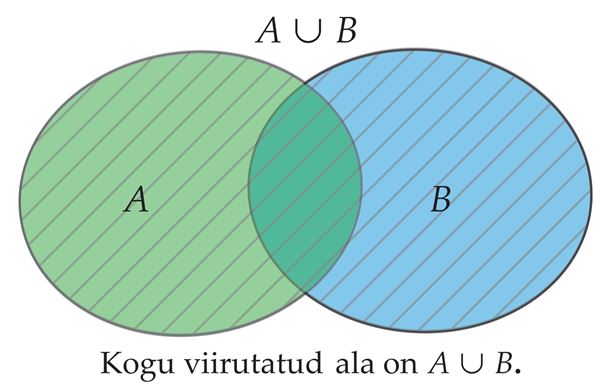
Märka

A ∪ ∅ = A

A ∪ A = A

Näide 2 

Leiame hulkade A ja B ühendi.

A = {b; d; e; f; h; i; k}

B = {a; b; e; f; i; k; l}

Ühend A ∪ B = {a; b; d; e; f; h; i; k; l}.

Näide 3 

Leiame hulkade

C = {x| –5 ≤ x ≤ –1} ja

D = {x| –3 < x < 3}

ühendi.

C ∪ D = {x| –5 ≤ x < 3} 

  • F = {1; 2; 3; 4; 5; 6; 7; 8; 9}
  • F = {1; 2; 3; 4; 5; 6; 7; 8}
  • F = {2}
  • F = {4; 6; 8}
  • F = {2; 3; 4; 5; 6; 7; 8}
  • F = {3; 5; 7}
  • F = {1; 3; 5; 7}
Seotud sisu
Muud tegevused

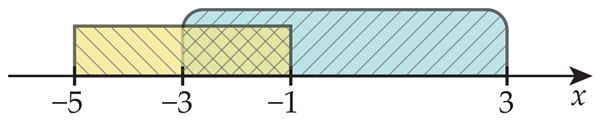
Hulkade ühine osa

Hulkade ühisosa

Kahe hulga A ja B ühisosaks A ∩ B nimetatakse hulka D, mille moodustavad kõik elemendid, mis kuuluvad nii hulka A kui ka hulka B.

D = A ∩ B

Operatsioon ja

Olgu x hulga D element, siis x kuulub samal ajal hulka A ja hulka B. Hulgateoorias pannakse see lause kirja nii:

x ∈ A ∩ B ⇔ (x ∈ A) ∧ (x ∈ B).

Loogilist operatsiooni ja tähistab sümbol ∧.

Hulkade ühisosa

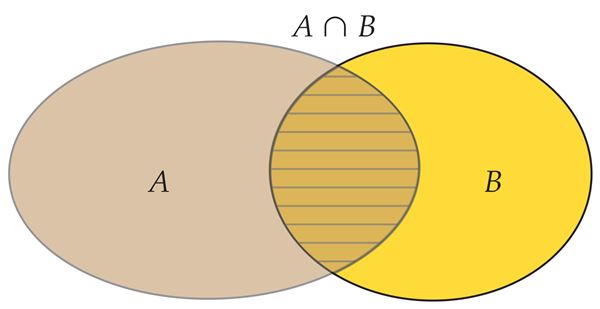
Märka

Kehtivad võrdused

A ∩ ∅ = ∅

A ∩ A = A

Näide 4

Leiame hulkade A ja B ühisosa.

A = {b; d; e; f; h; i; k}

B = {a; b; e; f; i; k; l}

Ühisoasa A ∩ B = {b; e; f; i; k}. 

Näide 5

Leiame hulkade

C = {x| –5 ≤ x ≤ –1} ja

D = {x| –3 < x < 3}

ühisosa.

C ∩ D = {x| –3 < x ≤ –1}

Mõtle

  • 1
  • 3
  • 8
  • 14

Vastus

10. klassis on  õpilast.

  • F = {1; 2; 3; 4; 5; 6; 7; 8; 9}
  • F = {1; 2; 3; 4; 5; 6; 7; 8}
  • F = {2}
  • F = {4; 6; 8}
  • F = {2; 3; 4; 5; 6; 7; 8}
  • F = {3; 5; 7}
  • F = {1; 3; 5; 7}
Seotud sisu
Muud tegevused

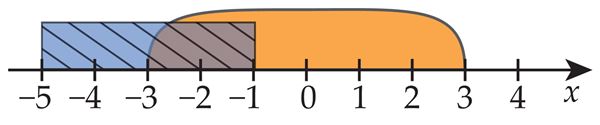
Elementide eemaldamine hulgast

Hulkade vahe

Kahe hulga A ja B vaheks nimetatakse hulka V, mille moodustavad kõik hulga A elemendid, mis ei kuulu hulka B.

V = A\B

Operatsioon vahe

Olgu x hulga V element, siis

x ∈ A ja x ∉ B.

Hulgateoorias pannakse see lause kirja nii:

x ∈ A\B ⇔ (x ∈ A) ∧ (x ∉ B).

Näeme, et hulgast A hulka B lahutades eemaldatakse hulgast A hulkade ühisosa A ∩ B elemendid

Mõtlemiseks

Uuri lauset

A ∩ B = ∅ ⇔ A\B = A, B\A = B

ja proovi see sõnastada.

Kahe hulga ühendi saab esitada kolme sellise hulga ühendina, millel pole ühiseid elemente.

Need on A\B, B\A ning ühisosa A ∩ B. 

A ∪ B = (A\B) ∪ (A ∩ B) ∪ (B\A)

Kolme hulga ühend

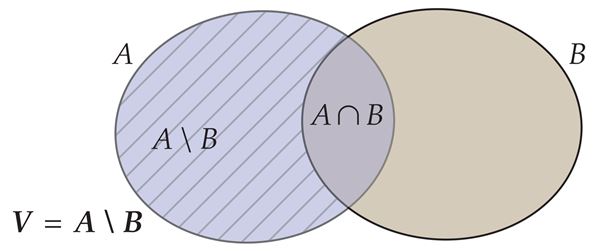
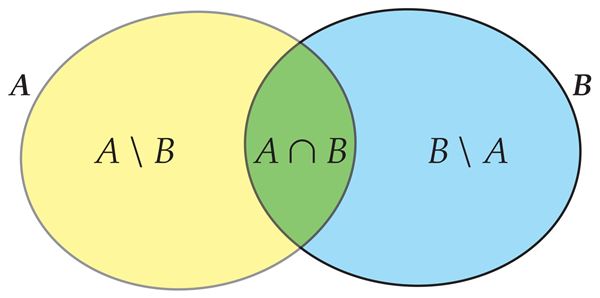
Märka

Hulkade vahe kaudu saab kirjeldada mingi hulga A osahulki, mis erinevad hulgast A vaid ühe või lõpliku arvu elementide poolest.

Näiteks viiest erinevate naturaalarvude hulk

B = ℕ\{5}.

Mõtle

  • M = {1; 2; 3; 4; 5; 6; 7; 8}
  • M = {2}
  • M = {4; 6; 8}
  • M = {2; 3; 4; 5; 6; 7; 8}
  • M = {3; 5; 7}
  • M = {1; 3; 5; 7}
  • K = {1; 2; 3; 4; 5; 6; 7; 8; 9}
  • K = {1; 2; 3; 4; 5; 6; 7; 8}
  • K = {2}
  • K = {2; 3; 4; 5; 6; 7; 8}
  • K = {3; 5; 7}
  • K = {4; 6; 8}
  • K = {1; 3; 5; 7}
  • K = {2; 4; 6; 8}
Seotud sisu
Muud tegevused

Harjuta ja treeni

      • {Peeter; Jüri}
      • {Peeter; Mari; Jüri}
      • {3 nime}
      • {Marit}
      • {Peeter}
      • {Pets}
      • {Jüri;Peeter}
      • {Peeter; Maris}
      • Tühi hulk
      • {Jüri; Mari}

      Hulgad on A = {2; 7; 14, 16} ja B = {5; 7; 10; 14; 15}. 

      • A ∪ B = {}
      • A ∩ B = {}

      Hulgad on A = {1; 11; 22; 33} ja B = {2; 22; 44; 66}. 

      Hulgad on A = {13; 16; 20; 25; 30} ja B = {10; 13; 20; 21; 25}.

      • A∪B={}
      • A∩B={}
      • A = {–3; –1; 0; 1; 4}
      • B = {–2; –1; 1; 2; 3}
      • C = {–2; 0; 1; 3; 4}
      • D = {–3; –1; 1; 2; 4}
      • E = (A ∪ B) ∩ (C ∪ D)
      • F = (A ∩ C) ∪ (B ∩ D)

      Vastus

      A = {b; d; e; f; h; i; k} ja B = {a; b; e; i; k: l}.

      • A\B = {; ; }
      • B\A = {; }

      Hulgad: C = {x| –5 ≤ x ≤ –1} ja D = {x| –3 < x < 3}. 

      • Vahe
        C\D = {x| x }.
      • Vahe
        D\C = {x| x }.

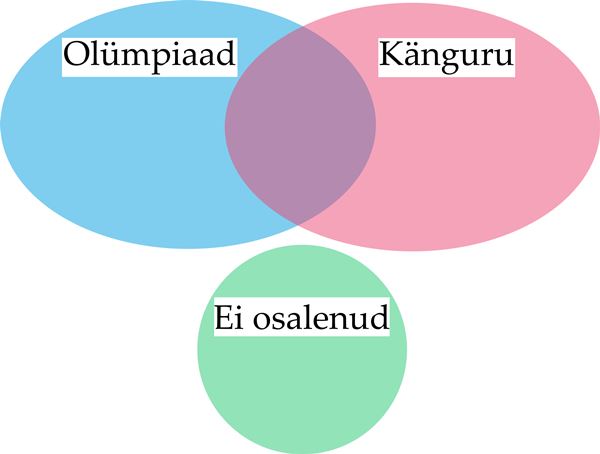
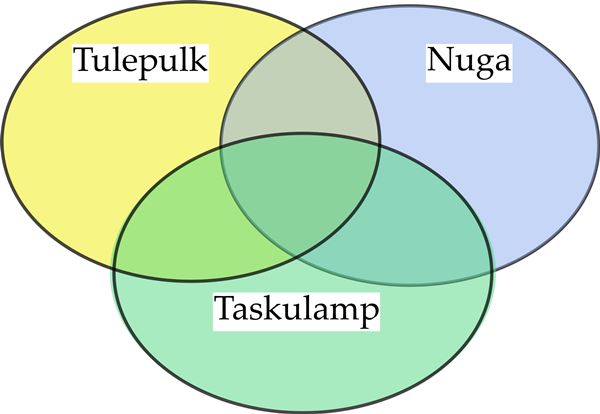
      10. klassi 42 õpilast said võimaluse osaleda ööpäevases laagris, mis õpetas, kuidas metsas hakkama saada. Muu varustuse hulgas oli kõigil kohustuslik kaasa võtta tulepulk, nuga ja taskulamp. Kui jõuti metsa, selgus, et kõik nimetatud kolm eset olid kaasas vaid viiel õpilasel. Tulepulk ja nuga oli ette näidata seitsmel õpilasel, nuga ja taskulamp 12 õpilasel. Tulepulga ja taskulambi võtsid kaasa kaheksa õpilast. Kokku oli laagri peale 11 tulepulka, 22 nuga ja 21 taskulampi.

      Mitu õpilast metsas hakkama saamise laagrisse ei ilmunud?

      • 1
      • 2
      • 3
      • 5
      • 6
      • 7
      • 8

      Vastus

      Laagris ei osalenud  õpilast.

      Seotud sisu
      Muud tegevused

      Valemid

      Seotud sisu
      Muud tegevused
      Palun oota