(Matem 7. kl)

Mis on ratsionaalarvud? Mida uut õpime?

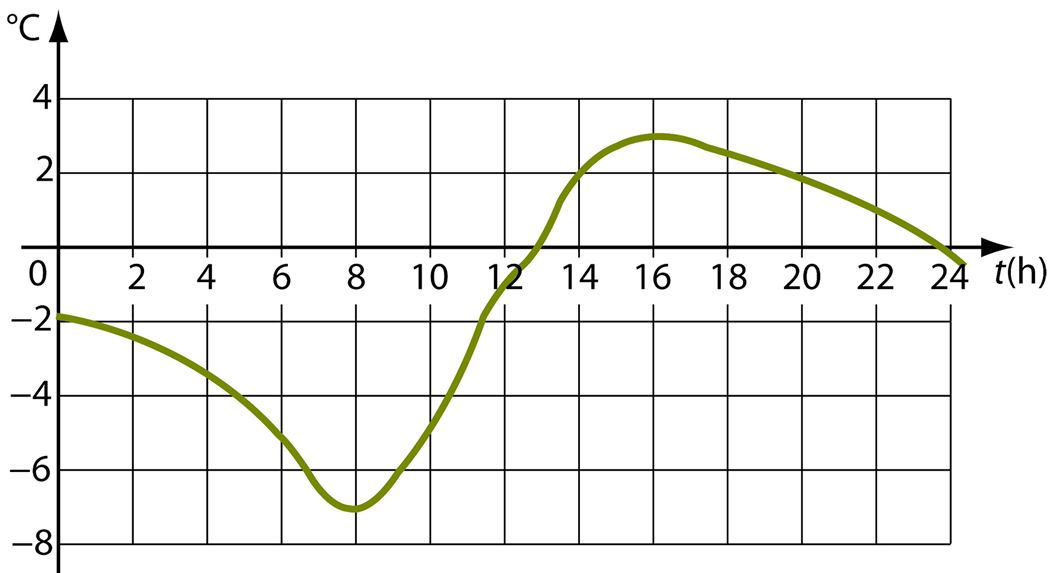
Me elame arvude keskel. Iga päev tuleb meil midagi loendada, mõõta ja arvutada. Mõtle, mida oled sina täna loendanud, mõõtnud või arvutanud.

Arve 0; 1; 2; 3; ... nimetatakse loomulikeks arvudeks ehk naturaalarvudeks. Neid kasutasid kindlasti juba enne kooli, kuid lähemalt õppisid nende omadusi tundma alles esimestes klassides. Naturaalarve saab alati liita ja korrutada, kuid lahutamis- ning jagamistehte vastust alati naturaalarvuga väljendada ei saa.

Selleks, et lahutada väiksemast naturaalarvust suuremat, on tarvis negatiivseid täisarve, mis on naturaalarvude vastandarvud. Nendega õppisid arvutama eelmisel aastal. Koos naturaalarvudega moodustavad need täisarvude hulga.

Selleks, et alati saaks jagada kahte täisarvu (v.a jagamine nulliga), on tarvis positiivseid ja negatiivseid murdarve. Murdarve ja täisarve kokku nimetatakse ratsionaalarvudeks. Nendega õpimegi selles teemas arvutama.

Pärast selle teema õppimist Sa tead, mis on

ratsionaalarvud,

arvu vastandarv,

arvu absoluutväärtus,

arvu aste,

ja Sa oskad

ratsionaalarve järjestada, liita, lahutada, korrutada ja jagada, kasutada tehete järjekorra reegleid ning liitmise ja korrutamise seadusi;
arvutada arvtelje kahe punkti vahelist kaugust ja ratsionaalarve sisaldavate tähtavaldiste väärtust;
arve astendada ja kasutada arvu 10 astmeid suurte arvude kirjutamisel;
lahendada tekstülesandeid ja lihtsamaid võrrandeid.

Seotud sisu

Sissejuhatav kordamine ja täiendamine

Suvevaheajal oled varemõpitust kindlasti mõndagi unustanud. Seepärast on Sul enne uue õppimist kõigepealt vaja oma teadmisi värskendada.

A()

B()

C()

D()

E()

G()

–23
3,8
–87
–7
14
–0,1
–27
23
100
–5,2
15
–14

Arv	Kaugus nullpunktist	Suund
$\|5\|$	ühikut
$\|- 6\|$	ühikut
$- \|- 2\|$	ühikut
$0, 7$	ühikut
$- \|1, 2\|$	ühikut
$- \|\frac{5}{6}\|$	$\frac{}{}$ ühikut
$\|- \frac{5}{8}\|$	$\frac{}{}$ ühikut
$\|0, 12\|$	ühikut
$\|0\|$	ühikut

–7 < 1

, , , , , ,

–2 < 5

, , , , ,

–7 < –1

, , , ,

–2,5 < 3,8

, , , , ,

–100,3 < –95,2

, , , ,

10 – 15 =

–25 + 15 =

–6 + (–7) =

–6 – 7 =

–21 – (–30) =

25 · (–3) =

–15 · 20 =

–12 · (–10) =

–14 · 15 =

11 · (–12) =

–42 : 14 =

75 : (–25) =

–36 : 18 =

–60 : (–10) =

42 : (–3) =

25 · (–2) – 49 =

–36 : 4 – 7 =

–3 · (6 – 10) – 12 =

56 : (–7) + 9 =

12 – 8 : 2 =

2 + (–7) – 12 – (–8) + 10 – 11 =

15 – 10 + 25 + 12 – 25 – 10 – 100 =

–14 – 6 – 25 + 40 + 25 – 20 =

125 – 25 + 28 + 52 – 16 – 4 + 95 =

Tähe väärtus	Tähtavaldise väärtus
n = –10	=
n = 50	=

Tähe väärtus	Tähtavaldise väärtus
m = –10	=
m = 5	=

x + 7 = 28
x =

t + 10 = –1
t =

10 – x = 7
x =

–10 – x = 7
x =

3t = 6
t =

–4t = 8
t =

2x = –10
x =

–3x = –9
x =

2n + 4 = 8
n =

2n + 6 = –10
n =

2x – 5 = 1
x =

2x – 6 = –4
x =

\|x\| = 5
\|x\| = 10
\|x\| = –5

–\|x\| = –10
\|–x\| = 2
\|–x\| = –1

Leia graafiku abil,

1) mitu kraadi näitas termomeeter

kell 3.00?	kell 12.00?	kell 20.00?	kell 5.30?
℃	℃	℃	℃

2) mis kellaajal oli temperatuur –3°, 0°, +2°;

–3° oli kell  ja kell ,
0° oli kell  ja kell ,
+2° oli kell  ja kell .

3) mis kellaajal oli temperatuur kõige madalam ja mitu kraadi see oli;

Kõige madalam oli temperatuur kell ja siis oli ℃.

4) mis kellaajal oli temperatuur kõige kõrgem ja mitu kraadi see oli;

Kõige kõrgem oli temperatuur kell ja siis oli ℃.

5) missugusel ajavahemikul näitas termomeeter külma, missugusel sooja;

Termomeeter näitas külma kella -st kella -ni ja sooja kella -st kella -ni.

6) kuidas muutus temperatuur ajavahemikus

kella 10-st 15-ni?

kella 2-st 8-ni?

7) missugusel ajavahemikul temperatuur langes, missugusel tõusis.

Temperatuur langes kella -st kella -ni ning kella -st kella -ni ja tõusis kella -st kella -ni.

$\frac{16}{20}$ = $\frac{}{}$

$\frac{9}{12}$ = $\frac{}{}$

$\frac{21}{35}$ = $\frac{}{}$

$\frac{13}{26}$ = $\frac{}{}$

$\frac{25}{75}$ = $\frac{}{}$

$\frac{36}{30}$ = $\frac{}{}$

$\frac{55}{100}$ = $\frac{}{}$

$\frac{3}{4}$ ja $\frac{1}{6}$

$\frac{3}{4}$ = $\frac{}{}$

$\frac{1}{6}$ = $\frac{}{}$

$\frac{3}{4}$ $\frac{1}{6}$

$\frac{2}{7}$ ja $\frac{5}{14}$

$\frac{2}{7}$ = $\frac{}{}$

$\frac{5}{14}$ = $\frac{}{}$

$\frac{2}{7}$ $\frac{5}{14}$

$\frac{7}{12}$ ja $\frac{5}{18}$

$\frac{7}{12}$ = $\frac{}{}$

$\frac{5}{18}$ = $\frac{}{}$

$\frac{7}{12}$ $\frac{5}{18}$

$\frac{11}{20}$ ja $\frac{13}{30}$

$\frac{11}{20}$ = $\frac{}{}$

$\frac{13}{30}$ = $\frac{}{}$

$\frac{11}{20}$ $\frac{13}{30}$

57 + 203 =

3002 – 9 =

195 + 405 =

128 – 38 =

0,8 – 0,25 =

1,24 + 3,06 =

2,74 – 1,7 =

3,8 + 6,2 =

4 · 205 =

2408 : 4 =

30 · 15 =

6000 : 20 =

1,6 : 4 =

0,8 · 0,05 =

0,2 : 0,01 =

1,6 : 0,8 =

$\frac{4}{7}$ + $\frac{3}{7}$ = $\frac{}{}$ =

$\frac{10}{11}$ – $\frac{5}{11}$ = $\frac{}{}$

$\frac{3}{5}$ + $\frac{1}{5}$ = $\frac{}{}$

$\frac{8}{15}$ – $\frac{1}{5}$ = $\frac{}{}$ = $\frac{}{}$

$\frac{12}{13}$ – $\frac{7}{13}$ = $\frac{}{}$

$\frac{8}{9}$ + $\frac{4}{9}$ = $\frac{}{}$ = $\frac{}{}$

3 – $\frac{2}{3}$ = $\frac{}{}$

$\frac{1}{2}$ + $\frac{1}{5}$ = $\frac{}{}$

$\frac{2}{3}$ ⋅ $\frac{1}{5}$ = $\frac{}{}$

$\frac{4}{5}$ : 3 = $\frac{}{}$

6 ⋅ $\frac{1}{6}$ =

4 : $\frac{1}{4}$ =

$\frac{3}{5}$ : $\frac{3}{4}$ = $\frac{}{}$

$\frac{5}{6}$ ⋅ $\frac{3}{5}$ = $\frac{}{}$

2 : $\frac{2}{3}$ =

$\frac{3}{10}$ ⋅ 5 = $\frac{}{}$ = $\frac{}{}$

$\frac{33}{100}$ =

$\frac{4}{5}$ =

$\frac{3}{10}$ =

$\frac{5}{8}$ =

2 $\frac{3}{4}$ =

1 $\frac{4}{25}$ =

3 $\frac{21}{50}$ =

0,7 = $\frac{}{}$

1,25 = $\frac{}{}$

0,36 = $\frac{}{}$

2,04 = $\frac{}{}$

0,65 = $\frac{}{}$

3,47 = $\frac{}{}$

1,205 = $\frac{}{}$

0,5 + $\frac{1}{3}$ =

$\frac{4}{5}$ – 0,3 =

$\frac{7}{12}$ + 0,25 =

$1 \frac{1}{2}$ – 0,15 =

3,6 + $\frac{5}{6}$ =

$2 \frac{3}{4}$ – 2,65 =

0,4 : $\frac{4}{15}$ =

$\frac{1}{6}$ ⋅ 0,45 =

$\frac{3}{8}$ : 1,25 =

$\frac{7}{12}$ ⋅ 0,9 =

$3 \frac{2}{5}$ : 0,17 =

5,1 : $\frac{3}{10}$ =

984 + 3926 =

4000 – 598 =

195 + 14 866 =

95 041 – 8704 =

4,807 + 0,39 =

5,1 – 2,88 =

3,06 – 0,158 =

15,4 + 38,63 =

47 · 529 =

7740 : 36 =

604 · 105 =

10 452 : 52 =

9,477 : 2,7 =

0,84 · 3,5 =

0,0704 : 0,11 =

0,61 · 1,12 =

Arvuta selle sõidu keskmine kiirus $(\frac{km}{h}),$ ümardades vastuse kümnendikeni.

Vastus. Selle sõidu keskmine kiirus oli $\frac{km}{h}$ .

Mitu täispööret tegi sellel teel tema jalgratta esimene ratas, mille diameeter oli 1,27 m? Ümarda vastus tuhandelisteni.

Vastus. Jalgratta esimene ratas tegi sellel teel ligikaudu täispööret.

Võrdle selle ratta diameetrit tänapäevaste jalgrataste omaga.

Rudolph Lewis

$\frac{1}{2}$ = %

$\frac{3}{4}$ = %

$\frac{9}{10}$ = %

0,35 = %

0,08 = %

$\frac{8}{100}$ = %

0,0045 = %

0,023 = %

Protsent	Kümnendmurd	Harilik murd
30%		$\frac{}{}$
45%		$\frac{}{}$
67%		$\frac{}{}$
80%		$\frac{}{}$

Protsent	Kümnendmurd	Harilik murd
100%		$\frac{}{}$
85%		$\frac{}{}$
22%		$\frac{}{}$
48%		$\frac{}{}$

(100; 10)	= %
(500; 25)	= %
(120; 12)	= %
(60; 4)	= %
(1200; 240)	= %

Vastus. Otepää kõrgustikust kuulub looduspargi koosseisu %.

Vastus. Kolmnurga pindala on cm².

1) 0, 3, 2, 5, 4, 7, 6, 9, , , ...

2) 3, 1, 4, 2, 5, 3, 6, 4, , , ...

Seotud sisu

Opiqus edenemine

	Tööd
	Peatükk on läbi töötatud

Mis on ratsionaal­arvud? Mida uut õpime?

Seotud sisu

Sisse­juhatav kordamine ja täiendamine

Seotud sisu

Lisa materjali

Lisatavad failid

Teata veast

Teata siia ainult Opiqu veast. Palun kirjelda viga nii täpselt kui võimalik.

Kui ootad Opiqu meeskonnalt vastust, lisa oma kontaktandmed (e-post, telefon).

Tee linnuke, et aidata meil spämmiga võidelda

Opiq kasutab küpsiseid

Mis on ratsionaalarvud? Mida uut õpime?

Sissejuhatav kordamine ja täiendamine