- Tuletise leidmine
- Algfunktsiooni mõiste
- Tuletise põhjal algfunktsiooni leidmine
- Funktsiooni avaldise taastamine
- Vabaliige ja selle mõju funktsioonile
Pöördoperatsioonid
Asume uurima diferentseerimise[mõiste: diferentseerimine – Tuletise arvutamine. Funktsiooni tuletis mingil kohal näitab selle funktsiooni väärtuse muutumise kiirust funktsiooni argumendi muutumisel — täpsemalt, funktsiooni tuletis on funktsiooni väärtuse muudu ja argumendi muudu suhte piirväärtus argumendi muudu lähenemisel nullile. ] pöördoperatsiooni, mida nimetatakse integreerimiseks.
Tuletise avaldisele saab seada vastavusse funktsiooni, mille tuletiseks see on. Selle operatsiooni tulemusena seatakse antud funktsioonile vastavusse selle algfunktsioon.
Funktsiooni f(x) algfunktsiooniks on funktsioon F(x), mille tuletiseks on antud funktsioon, st
F′(x) = f(x), x ∈ X,
kus X on funktsiooni f(x) määramispiirkond.
(x3 )′= 3x2. Järelikult, 3x2 algfunktsioon[mõiste: algfunktsioon – funktsioon, mille tuletiseks on antud funktsioon] on x3.
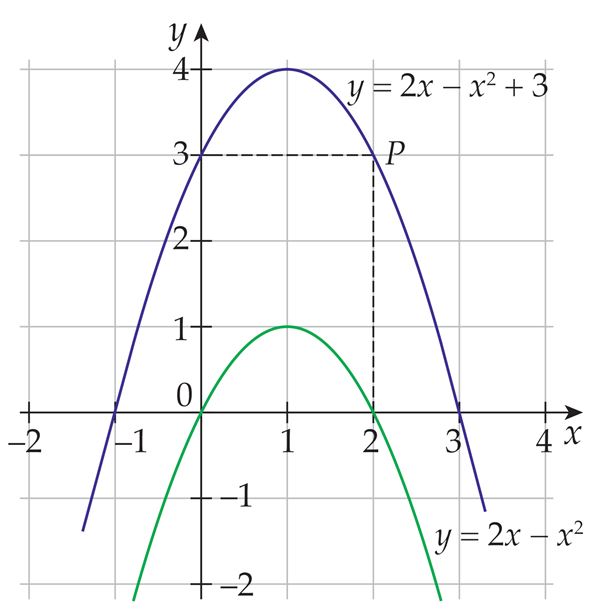
Kuid ka (x3 + 1)′ = 3x2, (x3 – 5)′ = 3x2 jne.
See näitab, et algfunktsioon pole üheselt määratud[mõiste: üheselt määratud – ainuvõimalikult]. Kui F(x) on funktsiooni f(x) algfunktsioon, siis ka (F(x) + C) on algfunktsioon, sest konstandi C tuletis on null:
(F(x) + C)′ = F′(x) + 0 = f(x).
Järelikult on antud funktsioonil lõpmatult palju algfunktsioone, mis erinevad vaid konstandi poolest.
Harjuta ja treeni
F1(x) = | f1(x) = |
F2(x) = | f2(x) = |
F3(x) = | f3(x) = |
F4(x) = | f4(x) = |
F5(x) = | f5(x) = |
F6(x) = | f6(x) = |
Reegel
(F(x) + C)′ = F′(x) + 0 = f (x)
Funktsiooni f(x) algfunktsiooniks on funktsioon F(x), mille tuletiseks on antud funktsioon.
Tuletiste tabel
f(x) | f′(x) | f(x) | f′(x) |
C |
| loga x |
|
xa |
| sin x |
|
ex |
| cos x |
|
ax |
| tan x |
|
ln x |
| cot x |
|