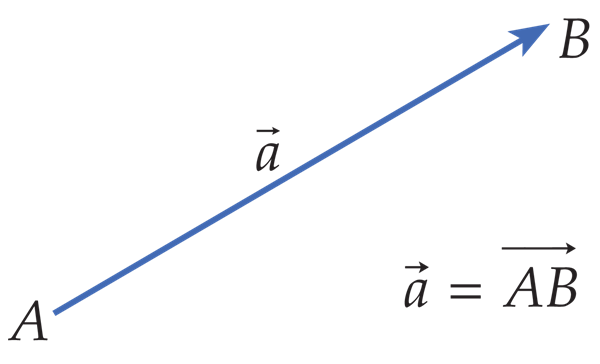
Suunatud sirglõik
Loodusseadusi kirjeldades tuleb ette kahte tüüpi suurusi. Ühtede iseloomustamiseks piisab vaid ühest arvust. Sellised suurused on näiteks mass, ruumala, temperatuur. Ühe arvväärtusega esitatavaid suurusi nimetatakse skalaarseteks suurusteks ehk skalaarideks[mõiste: skalaar – selle all mõistetakse matemaatikas arve või elemente, mis osalevad skalaariga korrutamises. Viimaseks on tarvis algebralist struktuuri, kus skalaariga korrutamine on defineeritud]. Teiste suuruste iseloomustamiseks aga ainult arvväärtusest ei piisa. Neid iseloomustab veel suund. Sellised suurused on näiteks jõud, kiirus ja kiirendus.
Suurusi, mida esitatakse nii arvväärtuse kui ka suuna kaudu, nimetatakse vektorsuurusteks ehk vektoriteks[mõiste: vektor – suurus, mida esitatakse nii arvväärtuse kui ka suuna kaudu].
Geomeetriliselt kujutatakse vektoreid nooltena, mille pikkus vastab suuruse arvväärtusele ja nool näitab selle suunda.
Seega, vektoriks nimetatakse suunatud sirglõiku.
Näide
Kui vektori alguspunkt on A ja lõpp-punkt B, siis vektorit võib kirjutad , kui aga vektorit tähistatakse ühe tähega, siis näiteks . Vektori ühetähelised tähistused on lühemad ja mugavamad.
Märka
Matemaatikas vaadeldakse vabavektoreid, st antud pikkuse ja suunaga vektori alguspunktiks võib olla mis tahes tasandi või ruumi punkt. Seejuures on see ikka sama vektor.
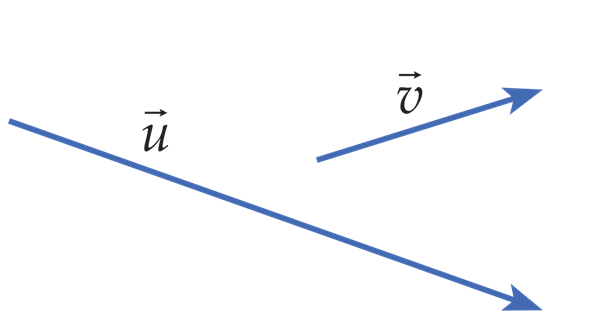
Samasihilisus
Peale suuna on vektoril olemas siht, mis sõltub vektorit kujutava suunatud lõigu asendist. Kuna vektor on suunatud lõik, siis võib vaadelda sirget, millel see lõik asub. See sirge määrabki vektori sihi.

Kui lõigule AB sirgel s anda suund punktist A punkti B, siis on see vektor . Või vastupidi, kui lõigule AB sirgel s anda suund punktist B punkti A, saame vektori .
Samal sirgel või paralleelsetel sirgetel asuvad vektorid on samasihilised.
Samasihilisi vektoreid nimetatakse kollineaarseteks[mõiste: kollineaarne – samasihiline] vektoriteks.
Kollineaarsust tähistatakse sama märgiga nagu paralleelsustki:
Kollineaarsed vektorid võivad olla samasuunalised või vastassuunalised.
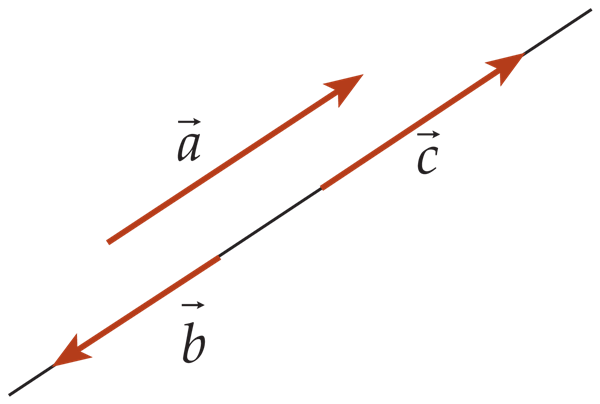
Võrdsus
Kaks vektorit on võrdsed, kui need on samasuunalised ja ühepikkused. Võrdsete vektorite vahele kirjutame võrdusmärgi.

Kaks vektorit on vastandvektorid, kui need on ühepikkused, kuid vastassuunalised.

Märka
Kui vektorit tähistatakse otspunktide kaudu, näiteks , siis vastandvektori[mõiste: vastandvektor – vektor, mis on antud vektoriga samasihiline, võrdse pikkusega, kuid vastassuunaga ] tähistuses on tähed vahetatud . Vastandvektorit tähistatakse veel miinusmärgiga (nagu vastandarvugi), st
= –.
Tunne ära
- erisihilised vektorid
- kollineaarsed vektorid
- võrdsed vektorid
- vastandvektorid