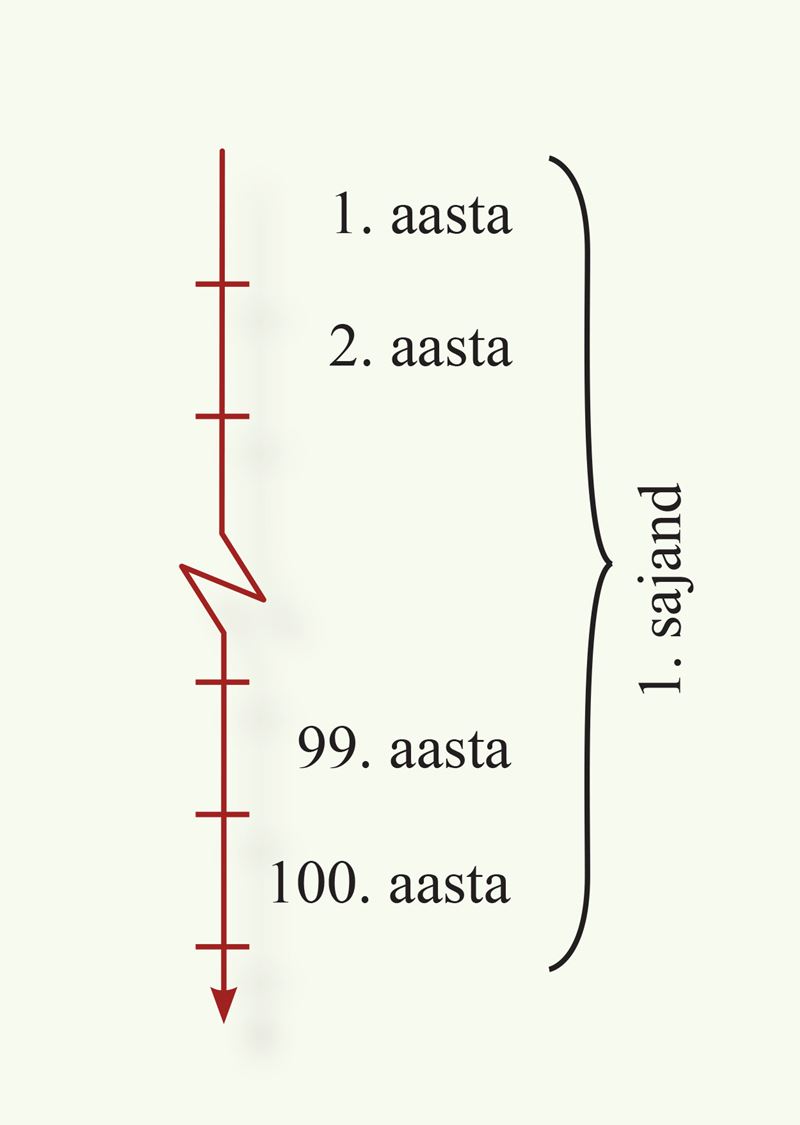
- Mitmendal sajandil ja mitmendal aastatuhandel (millenniumil) õpik ilmus?
Vastus. See õpik ilmus sajandil ja aastatuhandel. - Millal algasid eelmise küsimuse vastuses nimetatud sajand ja aastatuhat?
Vastus. Nimetatud sajand ja aastatuhat algasid aastal . - Millal algab pärast selle õpiku ilmumist uus sajand ja millal uus aastatuhat?
Vastus. Uus sajand algab aastal ja uus aastatuhat algab aastal . - Mitu aastat, kuud ja päeva on möödunud käesoleva sajandi algusest sel päeval, kui Sa lahendad seda ülesannet?
Vastus. Täna on möödunud käesoleva sajandi algusest aastat, kuud ja päeva.
 | ||||||

Vastus. Rukki perel tuleb novembris maksta kogu pere leiva eest € võrra rohkem kui oktoobris.
Vastus. Piima hind tõusis % võrra. Piima eest saadud sissetulek muutus % võrra.
- Kui palju maksab Artur tegelikult telefoni eest, kui ta ostab selle järelmaksuga? Kui mitme protsendi võrra on telefon järelmaksuga ostes kallim?
Vastus. Artur maksab järelmaksuga ostes telefoni eest eurot.
Järelmaksuga ostes on telefon % võrra kallim. - Tee vastavad arvutused ka Martini ostusoovi kohta.
Vastus. Martin maksab järelmaksuga ostes telefoni eest eurot.
Järelmaksuga ostes on telefon % võrra kallim. - Võrdle Arturi ja Martini ostusoove.

Vastus. Sääsetõrjevahendis on ‰ toimeainet.
Vastus. Peetril oli % võrra rohkem pooldajaid kui Ukul. Küsitluslehe jättis täitmata õpilast.