Koмбинаторика

Пример 1.

У малыша есть 5 карточек, на которых написаны пока еще незнакомые ему цифры 0, 1, 2, 3, 4. Он располагает в ряд три случайно взятые карточки. Какова вероятность того, что он выложит трехзначное число?

Для решения нужно найти число всех возможностей n и число благоприятствующих возможностей k.

Пример 1​. (прод.)

Решим задачу, сформулированную в примере 1.

Решение. Найдем число k возможностей, благоприятствующих событию, cocтоящему в появлении трехзначного числа. Для выбора первой цифры трехзначного числа имеется 4 возможности, так как 0 не может быть первой цифрой. После того, как первая цифра выбрана, можно выбрать любую из оставшихся 4 цифр, т. е. для выбора второй цифры имеется 4 возможности. После того, как выбраны первая и вторая цифры, есть 3 возможности для выбора третьей цифры. Поскольку должны быть выбраны как первая, так и вторая и третья цифры, то по правилу умножения получим, что всего можно составить 4 · 4 · 3 = 48 трехзначных чисел.

Рассуждая аналогично, мы видим, что из пяти цифр можно составить (располагая их подряд) n = 5 · 4 · 3 = 60 всевозможных комбинаций. Следовательно, соответствующая вероятность есть p = k : n = 48 : 60 = 0,8.

Пример 2.

Найдем, сколько автомобилей можно было бы зарегистрировать в Эстонии, если бы номер автомобиля состоял либо из четырех цифр, либо из четырех букв эстонского алфавита, за исключением букв Õ, Ä, Ö, Ü, Š, Ž.

Решение. По правилу умножения из цифр можно образовать 10 ⋅ 10 ⋅ 10 ⋅ 10 = 10⁴ различных номеров. Аналогично, из 26 букв можно образовать 26⁴ автомобильных номеров. Так как номера можно образовывать либо из цифр, либо из букв, то по правилу сложения получим, что всего можно было бы зарегистрировать 10⁴ + 26⁴ = 466 976 автомобилей.

Пример 3.

У маленького Пети есть четыре карточки с буквами Е, Л, О, С. Найдем, сколькими способами он может их упорядочить, т. е. сколько и каких «слов» он может составить из этих карточек.

Решение. Первую букву можно выбрать 4 различными способами, вторую – тремя, третью – двумя и четвертую - одним способом. По правилу умножения всего можно составить 4 · 3 · 2 · 1 = 24 слова. Приведем их список:

Пример 4.

Найдем с помощью калькулятора \frac{50!\cdot40!\cdot5!}{28!\cdot60!\cdot8!}.

Калькулятор, как правило, не позволяет найти значение такого выражения, найдя сначала значение числителя дроби. Уже при вычислении значения произведения 50! · 40! на табло появляется сообщение, что результат не помещается в памяти калькулятора. Этого можно избежать, если производить вычисления в таком порядке, при котором можно сохранять промежуточные результаты. Например, это можно сделать по следующей схеме:

50 !: 60 !· 40 !: 28 !· 5 !: 8 !=

и в результате получим 0,0291115274.

Пример 5.

Найдем, сколько четырехбуквенных «слов» можно составить из букв А, А, Б, Р. Некоторые из этих слов содержательны.

Метод решения, использованный в примере 3, здесь не подходит, так как при перестановке одинаковых букв «слово» не изменяется. 

Но можно выписать все эти «слова» и затем подсчитать их количество. Чтобы избежать ошибок, рекомендуется сделать это с помощью диаграммы «дерево», как показано на рисунке 1.1.

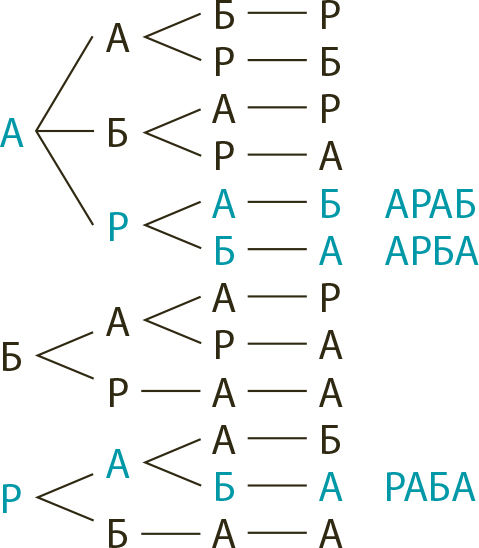Рис. 1.1