Liit­protsendiline kasvamine ja kahanemine

Vaatleme suurust, mille esi­algne väärtus a kasvab igas teatavas aja­vahemikus (näiteks aasta jooksul) p protsendi võrra aja­vahemiku alguses olnud väärtusest. Leiame, milline on selle suuruse väärtus n-nda aja­vahemiku lõpul:

esimese aja­vahemiku lõpuks on see a+\frac{p}{100}\cdot a = a\left(1+\frac{p}{100}\right),

teise aja­vahemiku lõpuks a\left(1+\frac{p}{100}\right)+\frac{p}{100}\cdot a\left(1+\frac{p}{100}\right) = a\left(1+\frac{p}{100}\right)^2,

kolmanda aja­vahemiku lõpuks a\left(1+\frac{p}{100}\right)^2+\frac{p}{100}\cdot a\left(1+\frac{p}{100}\right)^2 = a\left(1+\frac{p}{100}\right)^3.

Analoogia põhjal saame, et n-nda aja­vahemiku lõpul on vaadeldava suuruse väärtus

A_n=a\left(1+\frac{p}{100}\right)^n.   (1)

Kui n = 0, saame esi­algse väärtuse a. Avaldis (1) väljendab vaadeldava suuruse liit­protsendilist kasvamist. Nii kasvab hoius pangas, bio­mass noores metsas, bakterite arv katse­klaasis, inimeste arv Maal jne.

Näide 1.

Leiame, kui suureks kasvab raha­summa 1000 eurot 15 aasta jooksul, kui pank maksab aastas intressi 3%.

Et a = 1000, p = 3 ja n = 15, siis 15 aasta möödudes on pangas hoius

A_{15}=1000\cdot\left(1+\frac{3}{100}\right)^{15} = 1000\cdot1,03^{15} = 1557,97 eurot.

Kui mingi suuruse esi­algne väärtus a väheneb igas kindlas aja­vahemikus p protsendi võrra aja­vahemiku alguses olnud väärtusest, siis n sellise aja­vahemiku lõpuks on vaadeldava suuruse väärtus

A_n=a\left(1-\frac{p}{100}\right)^n.   (2)

Ka siin saame esi­algse väärtuse a, kui n = 0. Avaldis (2) väljendab liit­protsendilist kahanemist, mille kohaselt väheneb näiteks radio­aktiivse aine mass, samuti mingi masina või kogu tehase sisse­seade väärtus aja jooksul jne.

Näide 2.

Teatud radio­aktiivsest ainest laguneb öö­päevas 2%. Leiame, kui palju on seda ainet alles 4 öö­päeva möödudes, eeldusel, et esi­algu oli ainet 10 grammi.

Et tegemist on liit­protsendilise kahanemisega, siis 4. öö­päeva lõpuks on alles 10 · (1 – 0,02)4 = 10 · 0,984 ≈ 9,22 g radio­aktiivset ainet.

Näide 3.

Linnas elab 50 000 inimest. Mitme aasta pärast elab selles linnas kaks korda rohkem inimesi, kui igal aastal suureneb linna elanike arv 4% võrra?

Ülesande tingimuste kohaselt on 50\ 000\cdot\left(1+\frac{4}{100}\right)^n=100\ 0000 ehk 1,04^n=2.

Otsitavaks on astendaja n. Saadud võrrand on eksponent­võrrand, kuid seda ei saa lahendada nii nagu peatüki 3.1 näite 4 korral.

Et arv n on aastate arv, s.t naturaal­arv, siis võiksime tasku­arvutil leida järjest astmeid 1,042; 1,043; 1,044 jne. ning jälgida, millise n korral saab arvu 1,04 aste võrdseks arvuga 2 või ületab selle. Selleks sobib arvutus­skeem (osal arvutitel tuleb klahvile × vajutada vaid üks kord)

1,04 × (×) = = = … =,

kus­juures silmadega jälgime tablood ning mõttes loendame, mitu korda oleme klahvile = vajutanud. Ühe võrra suurem vajutuste arv (sest esimene vajutus annab 1,042) ongi otsitav n. Nii teinud, saame, et n = 18, sest 1,0417 ≈ 1,95, kuid 1,0418 ≈ 2,03. Ka tavalise proovimise teel on võimalik leida arvu n väärtust. Seega kahe­kordistub linna elanike arv 18 aasta jooksul.

Näide 4.

Auto maksis uuena 20 000 eurot. Mitme protsendi võrra väheneb igal aastal auto väärtus, kui kaheksa aasta pärast on selle auto väärtus 11 190 eurot?

Otsitavaks suuruseks on p%. Seega

20\ 000\cdot\left(1-\frac{p}{100}\right)^8=11\ 190 ehk \left(1-\frac{p}{100}\right)^8=0,5595, millest

1-\frac{p}{100}=\sqrt[8]{0,5595} ehk 1-\frac{p}{100}\approx0,92998.

Siit p ≈ 7.

Järelikult väheneb auto väärtus igal aastal keskmiselt 7% võrra.

Tähistame liit­protsendilisel kasvamisel esineva avaldise 1+\frac{p}{100} ja liit­protsendilisel kahanemisel esineva avaldise 1-\frac{p}{100} tähega b ning otsitava suuruse tähega y. Siis y = abn, kus­juures kasvamise korral on b > 1 ja kahanemise korral on 0 < b < 1 ning n ∈ N. Seega on liit­protsendiline kasvamine ja kahanemine esitatav funktsiooniga

y=ab^n,

kus argument n ∈ N.

Näide 5.

Funktsioon y = 2560 · 0,8n, n ∈ N esitab teatud suuruse liit­protsendilist kahanemist 20% võrra, sest b = 0,8 < 1; p = 20.

Funktsioon y = a · 2,5n, n ∈ N esitab liit­protsendilist kasvamist 150% võrra, sest b = 2,5 > 1; p = 150.

Näide 6.

Kui panka pandi alg­kapital 10 eurot ja pank maksab aastas 9% intressi, siis on iga aasta lõpul pangas raha­summa y = 10 · 1,09n (eurot), kus n ∈ N. Konstrueerime funktsiooni graafiku.

Vastav funktsiooni väärtuste tabel on järgmine:

Märgime arvu­paaridele vastavad punktid koordinaat­tasandile. Tulemuseks (joonis 3.1) on graafik. Punkte sujuva joonega ühendada ei tule, sest argumendil on vaid naturaal­arvulised väärtused.

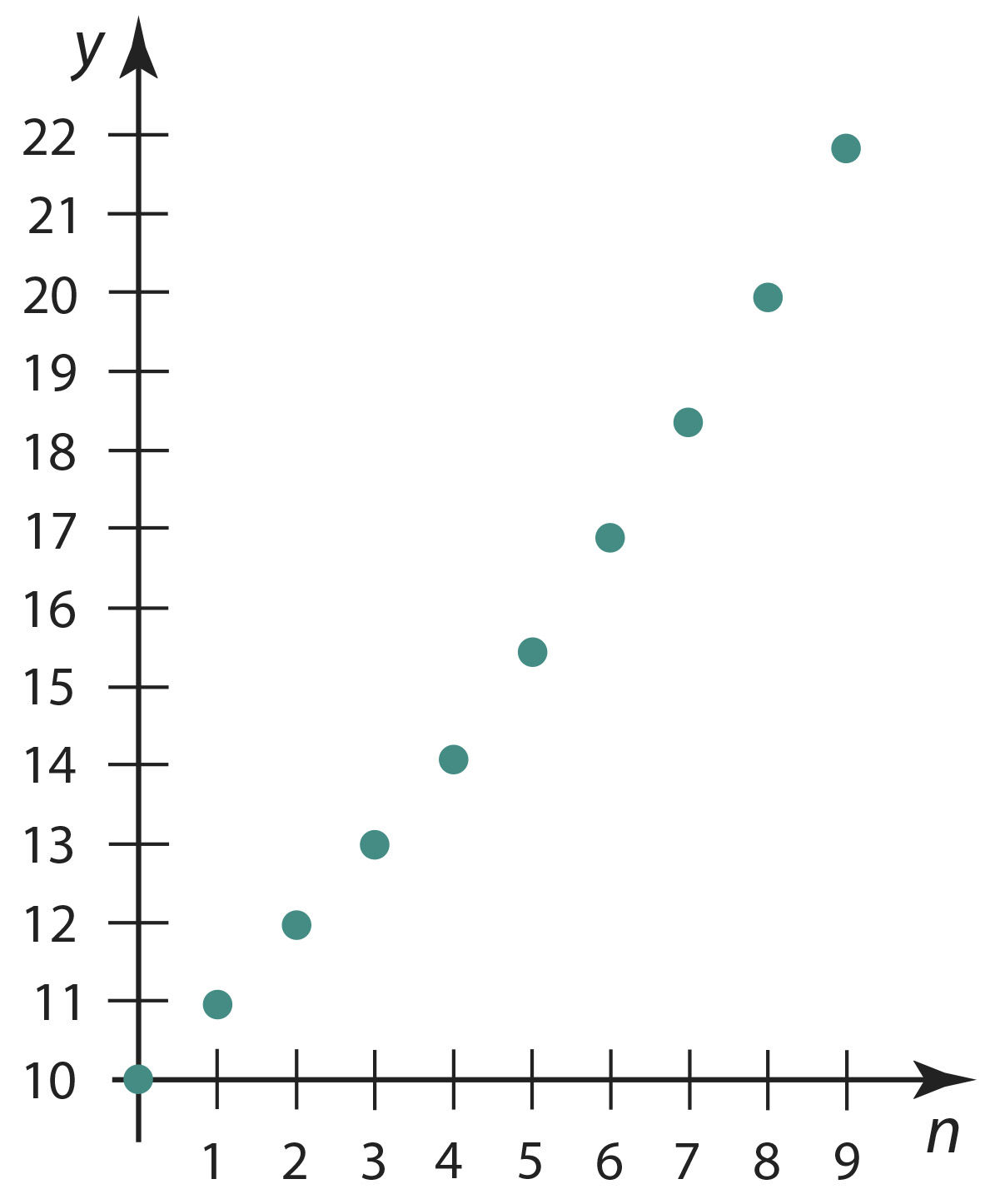Joon. 3.1
Еще на эту тему
Другие действия

Ülesanded A

Ülesanne 566. Hoiustamine

Vastus. Hoius kasvab  € suuruseks. Kui intressi makstakse ainult alg­summast, siis kasvab hoius  € suuruseks.

Ülesanne 567. Hoiustamine

Vastus. Selleks ajaks kasvab see hoius  € suuruseks.

Ülesanne 568. Puidu juurde­kasv

Vastus. Männikus on 20 aasta pärast  tm puitu.

Ülesanne 569. Puidu juurde­kasv

Vastus. Sellel metsa­tükil on siis  tm puitu.

Ülesanne 570. Mikroobide paljunemine

Vastus. Selles katse­klaasis on öö­päeva möödudes  mikroobi.

Ülesanne 571. Maa elanike arv

Vastus. Maa iga-aastane elanike juurde­kasv oli %. Kui Maa elanike arv kasvab edasi samas tempos, siis 7 miljardi piir ületatakse . aastaks.

Ülesanne 572. Maa elanike arv

Vastus. Arvestatud on % juurde­kasvuga. Maa elanike arv peaks kahe­kordistuma . aastaks ehk  a pärast.

Ülesanne 573. Tartu elanike arv

Vastus. Tartu elanik­kond kasvas keskmiselt % igal aastal. Eeldusel, et elanik­konna kasv toimub edasi samas tempos, elab 2030. aasta lõpus Tartus  inimest.

Ülesanne 574. Radio­aktiivse aine lagunemine
  1. esimese öö­päeva lõpul?

    Vastus. Alles on % esi­algsest kogusest.
  2. 21. öö­päeva lõpul?

    Vastus. Alles on % esi­algsest kogusest.
  3. 56. öö­päeva lõpul?

    Vastus. Alles on % esi­algsest kogusest.
Ülesanne 575. Masina väärtuse vähenemine
  1. 5 aasta möödudes?

    Vastus. 5 aasta möödudes on selle masina väärtus  €.
  2. 10 aasta möödudes?

    Vastus. 10 aasta möödudes on selle masina väärtus  €.
Ülesanne 576. Pärnu elanike arv

Vastus. Pärnu elanik­kond kahanes igal aastal keskmiselt %. Kui Pärnu elanik­kond väheneb edasi samas tempos, siis on Pärnus 2025 aasta lõpuks  elanikku.

Ülesanne 577. Inflatsioon

Kui palju „maksis” 1 kroon aasta lõpul, kui inflatsioon kuus oli 1%? Kui suur oli sellisel juhul inflatsioon aastas?

Vastus. Sel juhul „maksis” 1 kroon aasta lõpul  senti. Aastas oli inflatsioon %.

Ülesanne 578. Hoiustamine

Vastus. Hoius kahe­kordistub  aasta pärast

Ülesanne 579. Hoiustamine

Vastus. Pangas peab olema siis vähemalt  €.

Ülesanne 580. Hoiustamine

Vastus. See pank maksis aastas intressi %.

Ülesanne 581. Hoiustamine

Vastus. Panka tuleb paigutada  €

Еще на эту тему
Другие действия

Ülesanded B

Ülesanne 582. Raadiumi poolestus­aeg
  1. 3200 aasta möödudes?

    Vastus. Siis on alles % raadiumi kogusest.
  2. 4800 aasta möödudes?

    Vastus. Siis on alles % raadiumi kogusest.
  • Mõelge, kuidas tuleks leida, milline osa raadiumi kogusest on alles 800 a möödudes.

    Vastus. Siis on alles % raadiumi kogusest.
  • Hinnake, mitu protsenti meie aja­arvamise algusest Maal olnud raadiumi kogusest on praegu veel alles.

    Vastus. Praegu on veel alles umbes % meie aja­arvamise algusest Maal olnud raadiumi kogusest.
Ülesanne 583. Radio­aktiivse aine poolestus­aeg

Kui radio­aktiivse aine poolestus­aeg on T aja­ühikut ja tahetakse teada, kui palju radio­aktiivse aine kogusest C0 on alles t aja­ühiku möödudes (Ct), siis arvutatakse see valemi C_t=C_0\cdot0,5^{\frac{t}{T}} ehk C_t=C_0\cdot2^{-\frac{t}{T}} põhjal. Püüdke selgusele jõuda, milline on seos siin toodud avaldise ja liit­protsendilise kahanemise avaldise vahel.

Tšernobõli tuuma­jaama õnnetuses 1986. a aprillis toimus reostumine radio­aktiivse tseesiumiga, mille poolestus­aeg on 30 aastat. Mitu protsenti radio­aktiivset tseesiumi

  1. oli alles 10 aasta pärast?

    Vastus. 10 aasta pärast oli alles % radio­aktiivset tseesiumi.
  2. on alles täna­päeval?

    Vastus. Täna­päeval on alles % radio­aktiivset tseesiumi.
  3. on alles 2086. aasta aprilliks?

    Vastus. Siis on alles % radio­aktiivset tseesiumi.
Ülesanne 584. Hoiustamine

Kui pank maksab intressi p% aastas ja panka pannakse c eurot, siis \frac{1}{n} aasta möödudes on raha­summa suurus c\left(1+\frac{p}{100}\right)^{\frac{1}{n}} eurot. Leidke, kui suureks kasvab summa 1000 eurot 1) aastaga, 2) kuuga, 3) nädalaga, kui intress on 3%.


  1. Vastus. Aastaga kasvab summa  euroni.

  2. Vastus. Kuuga kasvab summa  euroni.

  3. Vastus. Nädalaga kasvab summa  euroni.
Ülesanne 585. Hoiustamine

Vastus. Selleks peab pangas olema vähemalt  €.

Ülesanne 586. Paagis oleva vedeliku kogus

Mitu liitrit vedelikku on paagis alles

  1. 2. ööpäeva lõpul?

    Vastus. Paagis on alles  liitrit vedelikku.
  2. 11. ööpäeva lõpul?

    Vastus. Paagis on alles  liitrit vedelikku.
Ülesanne 587. Liit­protsendiline muutumine

Ülesanne 588. Liit­protsendiline muutumine

Vastus. q = 

Kui suur on puu juurde­kasv viie aasta jooksul, kui esimesel aastal kasvas puu 50 cm võrra ning igal järgmisel aastal oli juurde­kasv 20% võrra väiksem kui eelmisel aastal?

Vastus. Puu juurde­kasv viie aasta jooksul on  cm.

Еще на эту тему
Другие действия