Теорема Фалеса

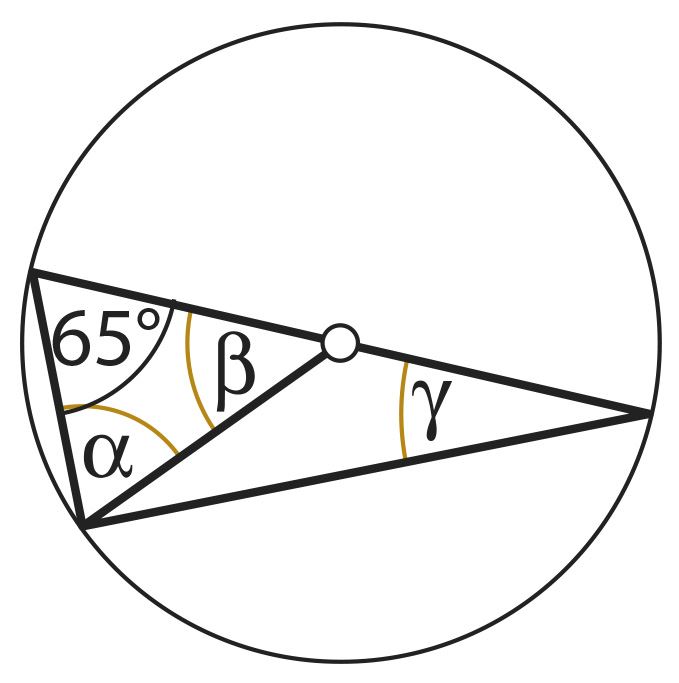
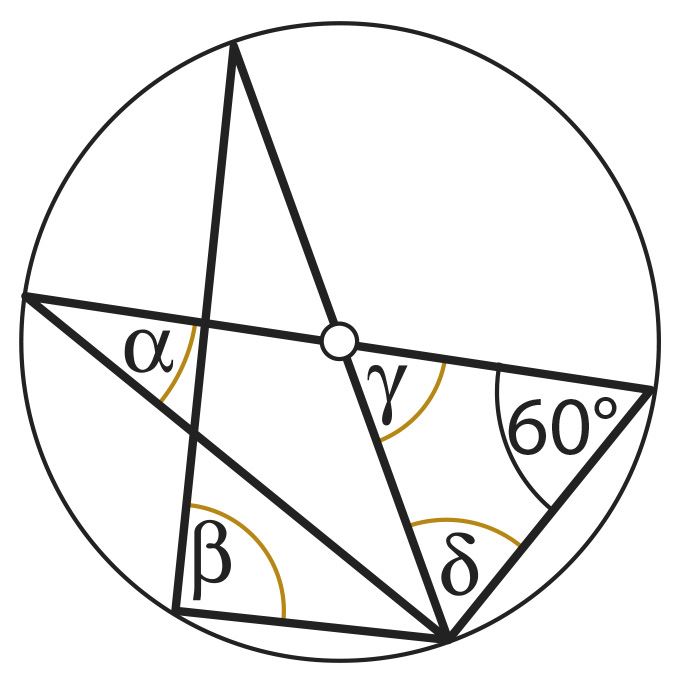
Если ты ответил правильно на все вопросы предыдущей задачи и обосновал ответы, то тем самым ты доказал, что

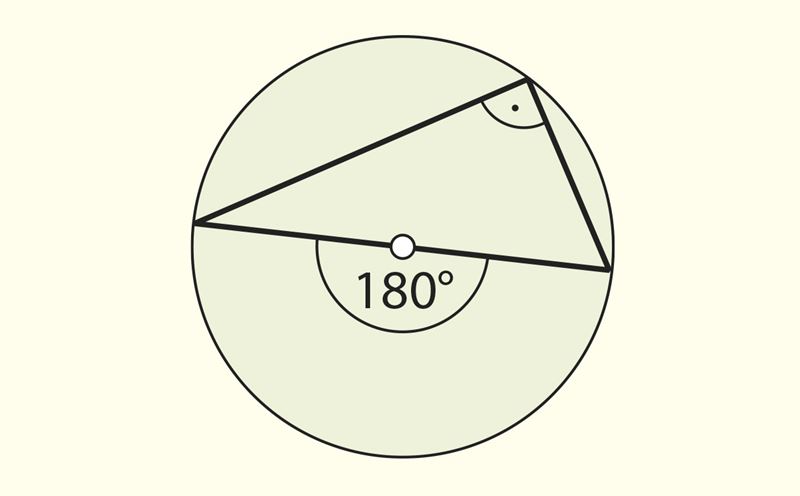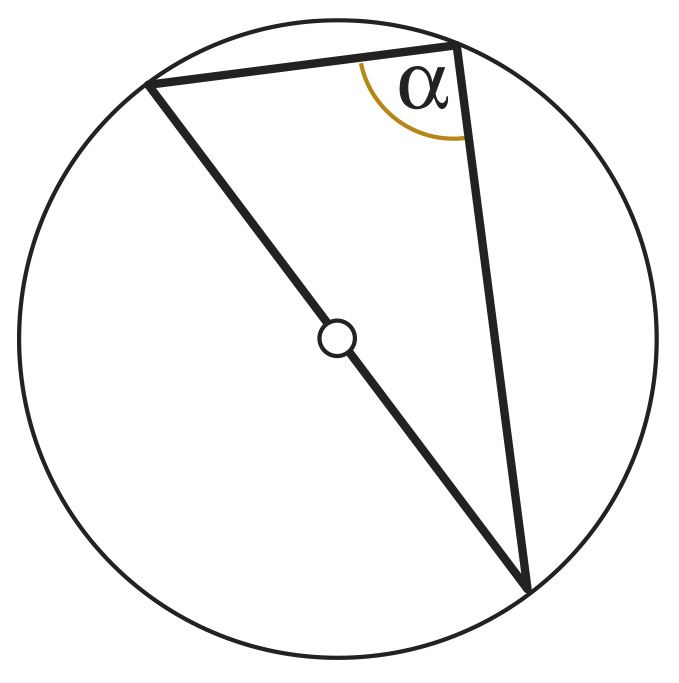
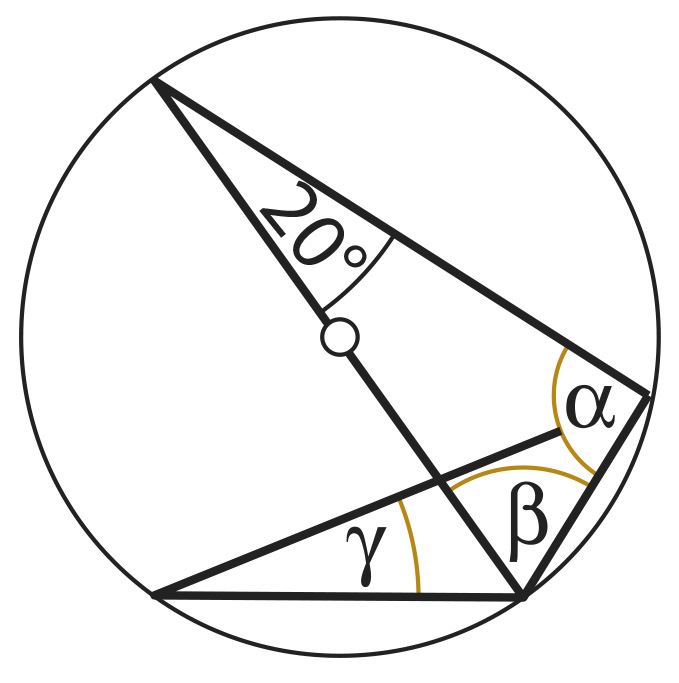
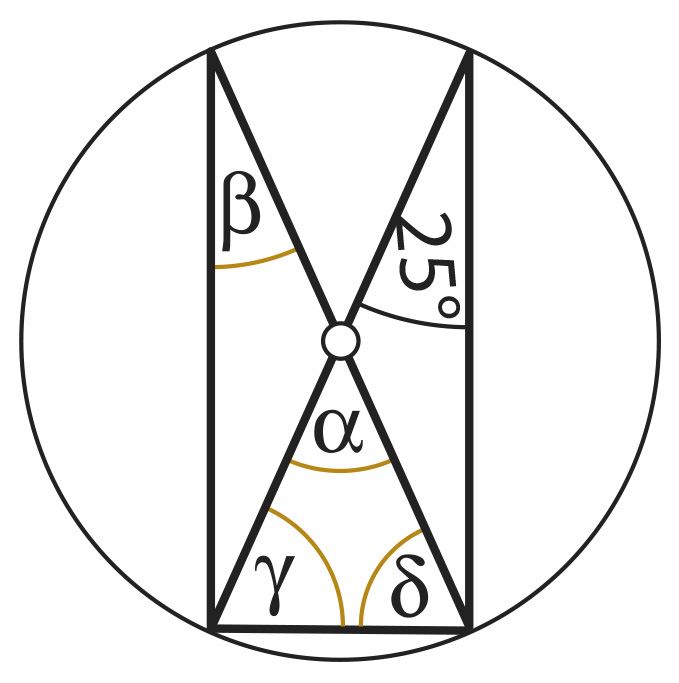
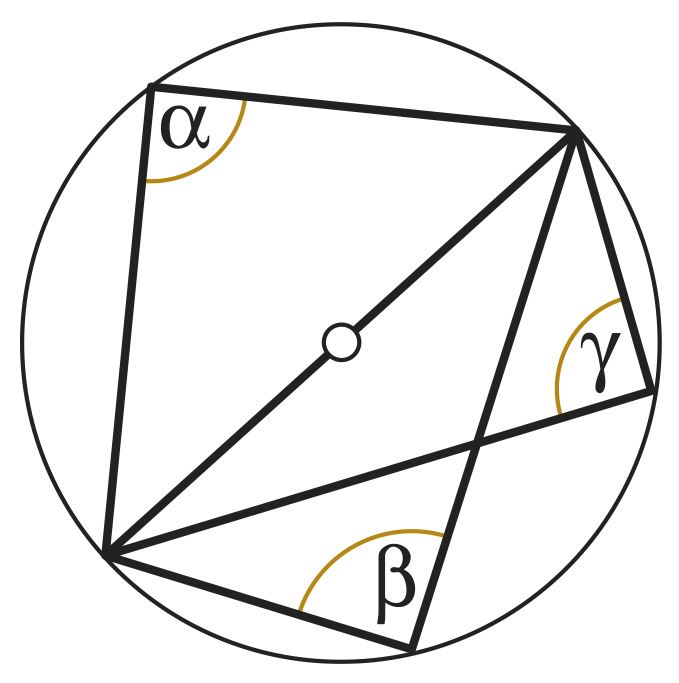
вписанный в окружность угол, опирающийся на полуокружность (или на диаметр), является прямым углом.

Это предложение называют теоремой Фалеса.

Фалес Милетский (ок. 625 – 547 г. до н.э.) – древнегреческий математик и философ. Известна также другая теорема Фалеса (см. § 5.3).

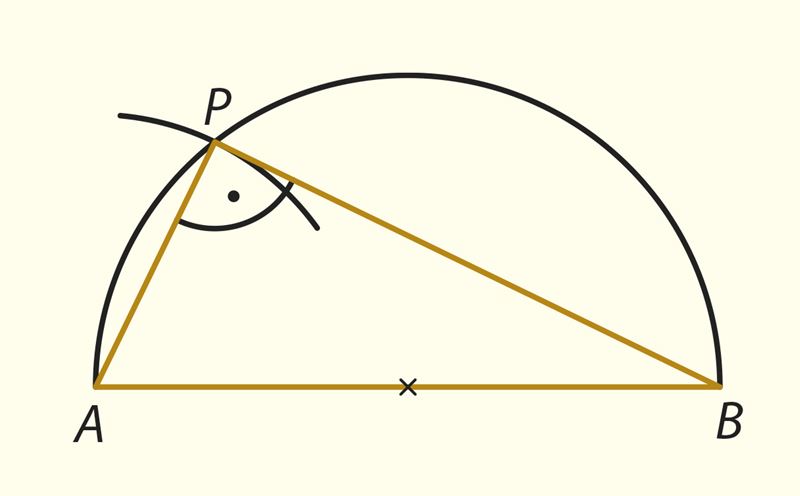
С ее помощью легко построить прямоугольный треугольник, если известны его гипотенуза и один из катетов. Для этого начертим полуокружность, диаметром которой является заданная гипотенуза AB. Затем раствором циркуля, равным заданному катету, опишем дугу окружности с центром в точке A, пересекающую первую окружность. Полученная точка пересечения P и будет третьей вершиной искомого треугольника ABP, а именно, вершиной прямого угла.

Из сказанного выше следует также еще один признак равенства прямоугольных треугольников (кроме ранее известных):

если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то эти треугольники равны.

Упражнения A

974. GeoGebra

Убедись в справедливости теоремы Фалеса с помощью программы GeoGebra.

975. Перегибание бумаги

Покажи справедливость теоремы Фалеса с помощью перегибаний бумаги. Начерти циркулем на бумаге окружность. Вырезáть ее из бумаги не нужно. Обозначь центр окружности и перегни ее по диаметру. Обозначь концы диаметра А и В и отметь на окружности точку С. Перегни бумагу по двум хордам АС и ВС.

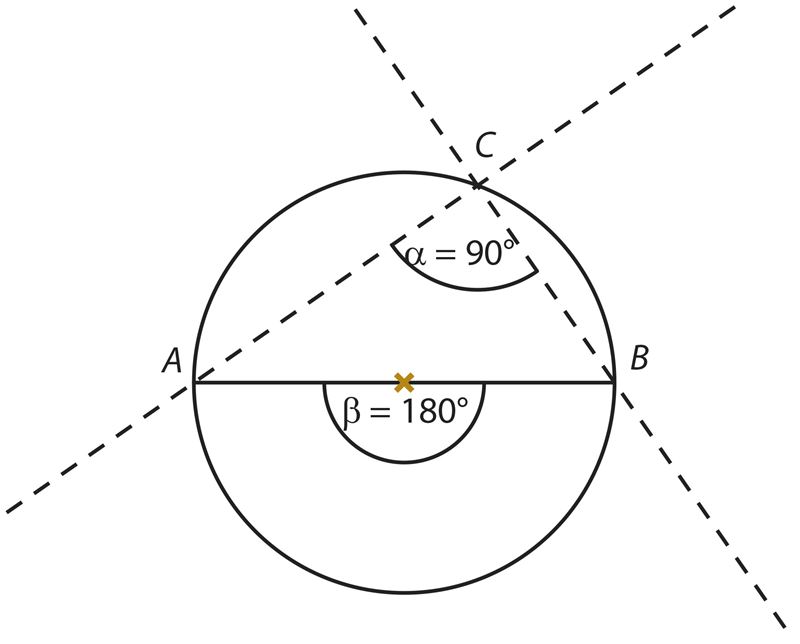
Теперь сложи вдвое лист бумаги по прямой АС. Как видно, прямая ВС накладывается на себя. Поэтому прямые АС и ВС перпендикулярны. Следовательно, перпендикулярны и хорды, расположенные на этих прямых.

Обозначь на бумаге вписанный угол и центральный угол, а также запиши их величины.

α = °

β = °

γ = °

α = °

β = °

γ = °

δ = °

α = °

β = °

γ = °

α = °

β = °

γ = °

α = °

β = °

γ = °

δ = °

c = 50 мм, a = 30 мм.

Измерь на полученном чертеже второй катет и вычисли площадь треугольника.

Ответ: S ≈ мм²

c = 42 мм, a = 28 мм.

Измерь на полученном чертеже второй катет и вычисли площадь треугольника.

Ответ: S ≈ мм²

c = 6,2 см, a = 4,1 см.

Измерь на полученном чертеже второй катет и вычисли площадь треугольника.

Ответ: S ≈ см²

c = 7,6 см, a = 5,2 см.

Измерь на полученном чертеже второй катет и вычисли площадь треугольника.

Ответ: S ≈ см²

AB = 50 мм, ∠A = 30°.

Сделай нужные измерения и вычисли площадь треугольника.

Ответ: S ≈ мм²

AB = 46 мм, ∠A = 70°.

Сделай нужные измерения и вычисли площадь треугольника.

Ответ: S ≈ мм²

AB = 4,2 см, ∠A = 52°.

Сделай нужные измерения и вычисли площадь треугольника.

Ответ: S ≈ см²

AB = 6,8 см, ∠A = 6,5°.

Сделай нужные измерения и вычисли площадь треугольника.

Ответ: S ≈ см²

Упражнения Б

980.1 Задача на построение

Пользуясь только циркулем и линейкой, построй прямоугольный треугольник, у которого гипотенуза равна 10 см и один из катетов равен 4 см.

980.2 Задача на построение

Пользуясь только циркулем и линейкой, построй окружность радиуса 3 см и прямоугольник, все вершины которого лежат на окружности и одна из сторон равна 4 см.

980.3 Задача на построение

Пользуясь только циркулем и линейкой, построй квадрат, диагональ которого равна 7 см.

981. Задача на построение

Построй прямоугольный треугольник, у которого гипотенуза AB = 56 мм, а проведенная к гипотенузе высота пересекает ее в точке, удаленной от вершины A на 3,8 см.

Теорема Фалеса

More like this