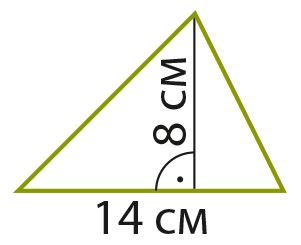
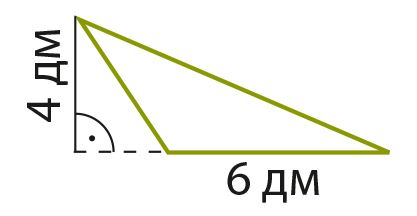
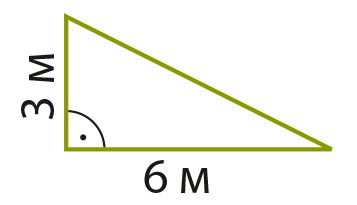
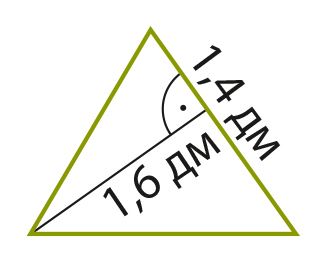
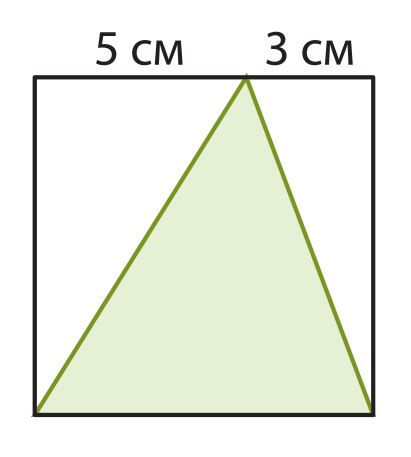
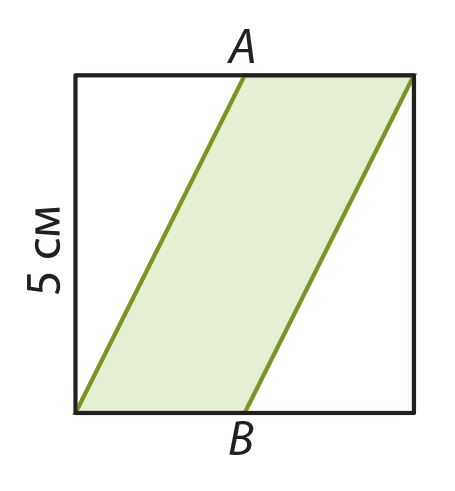
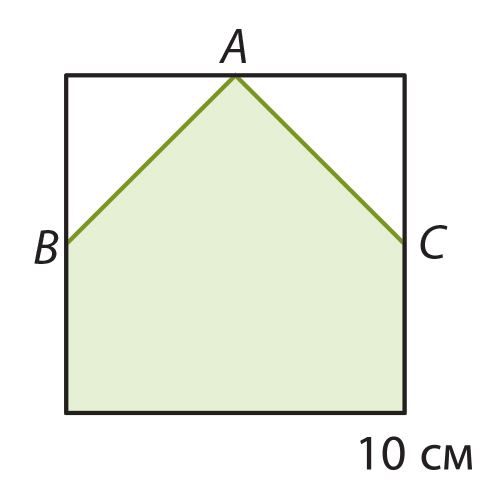
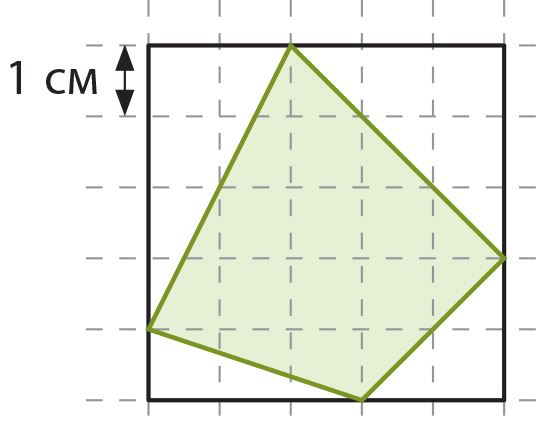
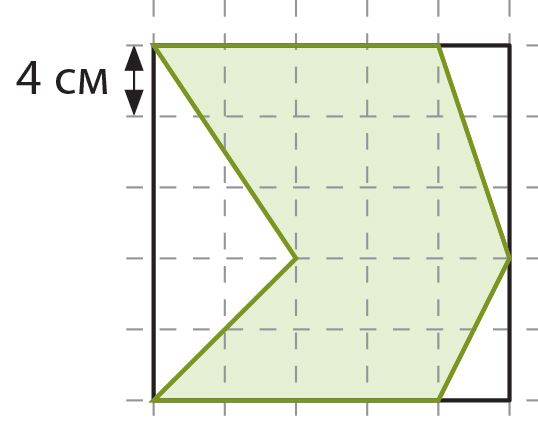
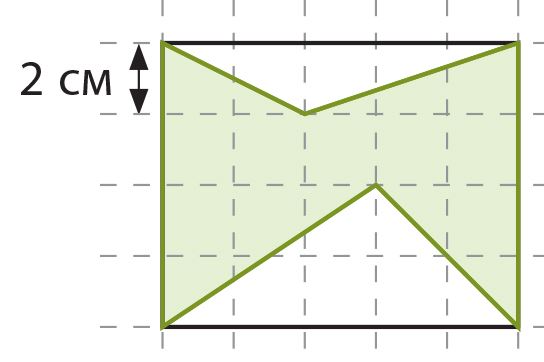
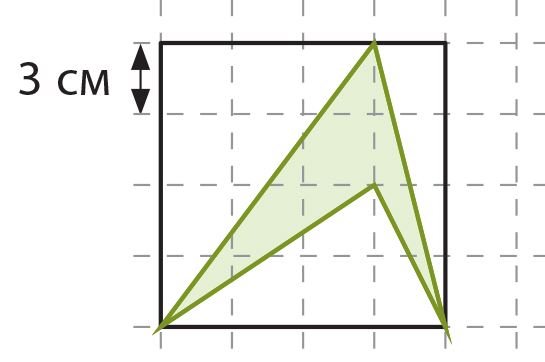
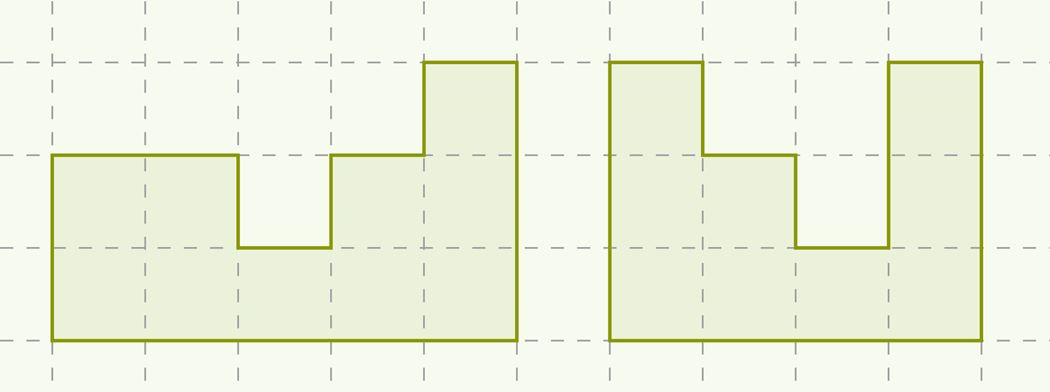
Вспомни, что такое площадь фигуры и как она вычисляется. Площадь какой фигуры на рисунке больше? Сравни также периметры этих фигур.
 | ||||||
Вспомни также, как вычисляется площадь прямоугольника и сформулируй соответствующее правило.
 | ||||||||
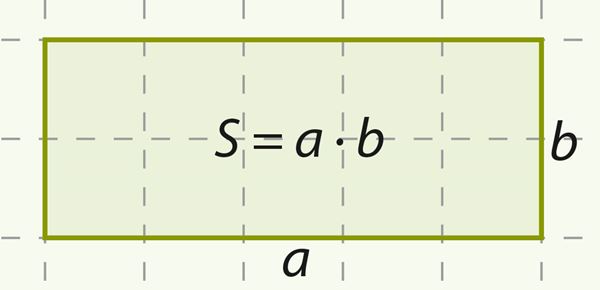А как вычислить площадь треугольника? Чтобы понять это, выполни практическую работу.
- Начерти на отдельном листе бумаги два каких-нибудь равных треугольника и проведи в каждом из них по одной высоте к соответственно равным сторонам.
- Вырежи один из треугольников и наклей его в тетрадь. Обозначь высоту этого треугольника буквой h, а основание – буквой a.
- Вырежи второй треугольник и разрежь его вдоль высоты на два прямоугольных треугольника 1 и 2. Приклей эти треугольники вплотную к первому треугольнику так, как показано на рисунке справа.
- Внимательно изучи следующий текст.
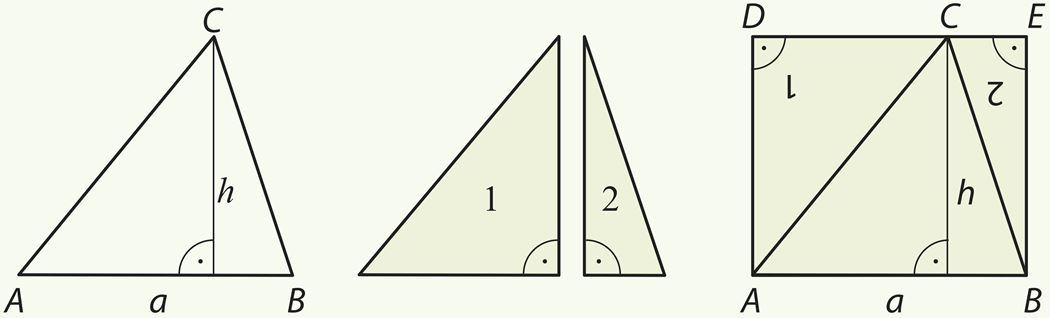
Выполнив указанную работу, мы получили четырехугольник ABED. Этот четырехугольник является прямоугольником. Сторона AB (или DE) этого прямоугольника равна основанию a исходного треугольника, а сторона BЕ (или AD) равна высоте h исходного треугольника. Площадь прямоугольника равна произведению ah. Прямоугольник составлен из двух пар равных треугольников, значит площадь S исходного треугольника равна половине площади прямоугольника.
Следовательно,
Площадь треугольника равна половине произведения основания на высоту.
Это правило справедливо для вычисления площади любого треугольника, независимо от его вида. В качестве высоты прямоугольного треугольника можно взять один из катетов, тогда основанием будет другой катет.
 | ||||||||
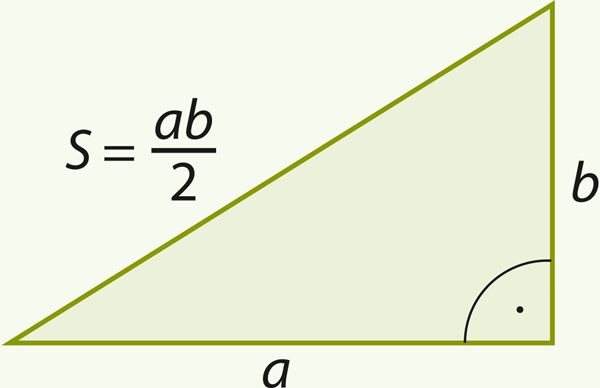Таким образом,
площадь прямоугольного треугольника равна половине произведения его катетов:
Площадь прямоугольного треугольника можно вычислить и по-другому, проведя высоту к гипотенузе. Тогда получим:
 | ||||||||
 |
||||||||
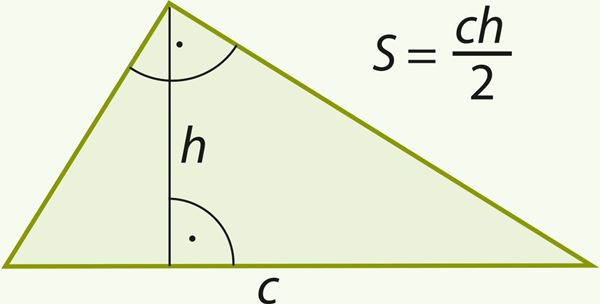Вычислим площадь треугольника с основанием 5,6 cм и высотой 3,5 cм.
Решение. По формуле площади треугольника получим:
(см2).
Ответ: площадь треугольника равна 9,8 см2.
 |
||||||||
Площадь прямоугольного треугольника равна 18 cм2, а один из катетов равен 8 cм. Вычислим длину второго катета.
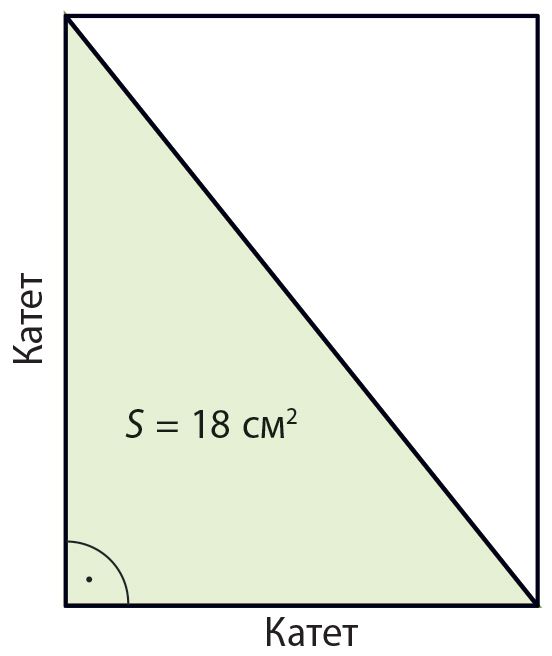
Решение. Обозначим длину второго катета буквой a. Получим уравнение: , или 4a = 18, откуда a = 18 : 4 = 4,5 (cм).
Ответ: длина второго катета равна 4,5 cм.
Упражнения A
 |
||||||||
1) как вычислить площадь треугольника;
2) как можно вычислить площадь прямоугольного треугольника.
Ответ: S = см2
Ответ: S = дм2
Ответ: S = м2
Ответ: S = дм2
Основание и высота | Площадь |
a = 5 cм, h = 12 cм | cм2 |
a = 0,6 м h = 0,4 м | м2 |
a = 48 мм, h = 5,5 cм | cм2 |
a = 34 м, h = 42 м | м2 |
a = 8,4 дм, h = 62 cм | cм2 |
a = 250 cм, h = 3,8 м | м2 |
Катеты | Площадь | ||
4 cм и 6 cм | cм2 | ||
9 дм и 8 дм | дм2 | ||
5 м и 7 м | м2 | ||
Катеты | Площадь | ||
9,8 дм и 10,5 дм | дм2 | ||
17,5 м и 240 cм | м2 | ||
6,9 м и 72 дм | дм2 | ||
- Бабушка согласилась пришить на штаны внуку Вове две красные треугольные заплаты только в том случае, если Вова вычислит площади этих заплат. Вова измерил заплатки и выяснил, что у одного треугольника основание равно 16,4 см и высота – 12 см, а у другого основание равно 24 см и высота – 8,2 см. Вова вычислил площади и получил заплаты.
Ответ: площадь первой заплаты равна cм2, а площадь второй – cм2. - Мама сшила платок в форме равнобедренного прямоугольного треугольника, меньшая сторона которого 8 дм. Сколько квадратных дециметров ткани ушло на платок?
Ответ: ткани ушло дм2. - Папа застеклил окна на чердаке. Для этого ему пришлось вырезать 8 треугольных стекол в виде прямоугольного треугольника с катетами 38 см и 25 см. Сколько квадратных дециметров стекла было использовано?
Ответ: стекла потребовалось дм2.
Ответ: высота треугольника равна см, а его площадь – см2.
Ответ: высота, проведенная к основанию, равна см, а площадь треугольника равна см2.
Ответ: высота, проведенная к боковой стороне, равна см, а площадь треугольника равна см2.
Ответ: проведенная к этой стороне высота равна см, а площадь треугольника равна см2.
Ответ: S = дм2.
В прямоугольном треугольнике один из катетов равен 15,6 м, а второй катет составляет первого. Вычисли площадь треугольника.
Ответ: S = м2.
Упражнения Б
 |
||||||||
Ответ: со всего поля собрали т ржи.
Ответ: площадь участка равна м2.
1 дм = 10 cм
1 дм2 = 102 cм2 = 100 cм2
1 м = 10 дм
1 м2 = 102 дм2 = 100 дм2
Данные величины | Сторона a |
h = 4,8 cм, S = 20,4 cм2 | cм |
h = 26 дм, S = 234 дм2 | дм |
Данные величины | Сторона a |
h = 65 дм, S = 23,4 м2 | м |
h = 0,82 дм, S = 22,55 cм2 | cм |
Данные величины | Высота h |
a = 7 м, S = 28 м2 | м |
a = 1 м, S = 50 дм2 | дм |
a = 4,5 м, S = 180 дм2 | дм |
a = 6,8 дм, S = 357 cм2 | cм |
Данные величины | Искомый катет |
a = 4 cм, S = 12 cм2 | cм |
a = 5,2 дм, S = 20,8 дм2 | дм |
Данные величины | Искомый катет |
a = 20 дм, S = 3 м2 | м |
a = 3,6 дм, S = 180 cм2 | cм |
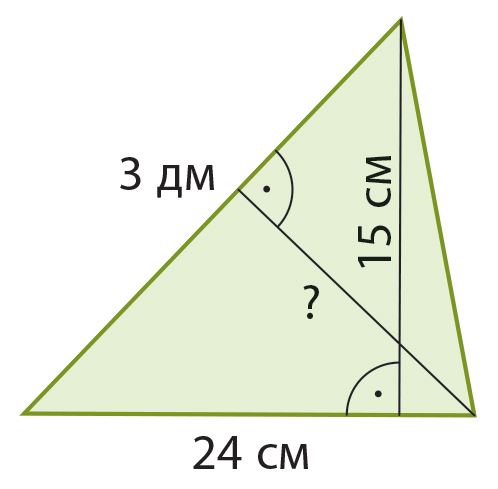
Ответ: проведенная ко второй стороне высота равна см.
Ответ: другая сторона равна см.
Ответ: высота, проведенная к стороне ML, равна м.
Ответ: сторона BC равна дм.
Ответ: второй катет равен см, а высота, проведенная к гипотенузе, – см.
- 6 дм, 8 дм и 10 дм;
Ответ: высота равна дм. - 12 м, 16 м и 20 м.
Ответ: высота равна м.
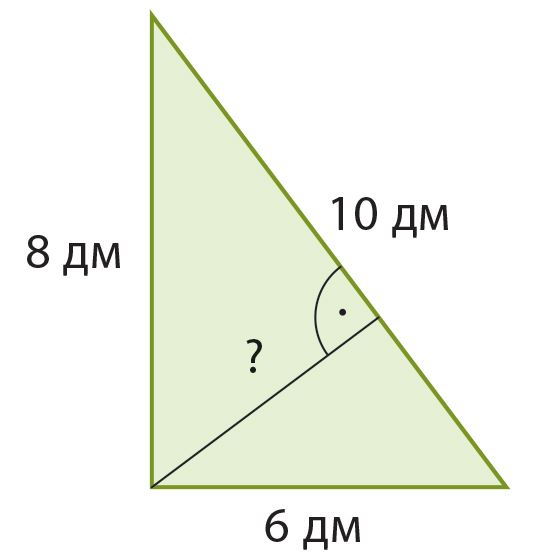
Ответ: боковая сторона равна см.
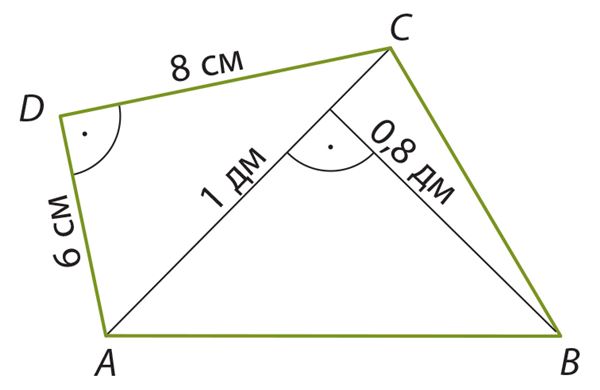
Ответ: площадь четырехугольника равна см2.
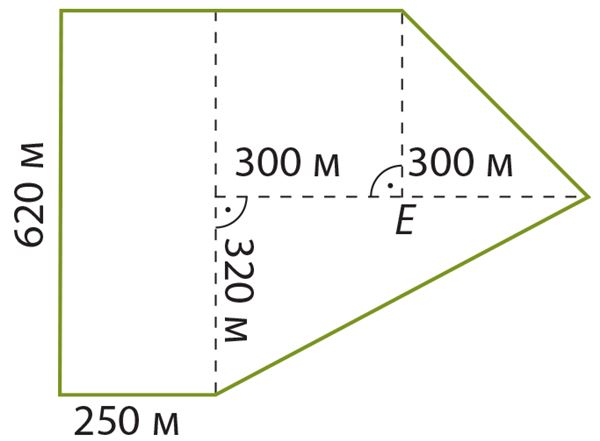
Ответ: площадь участка равна га.
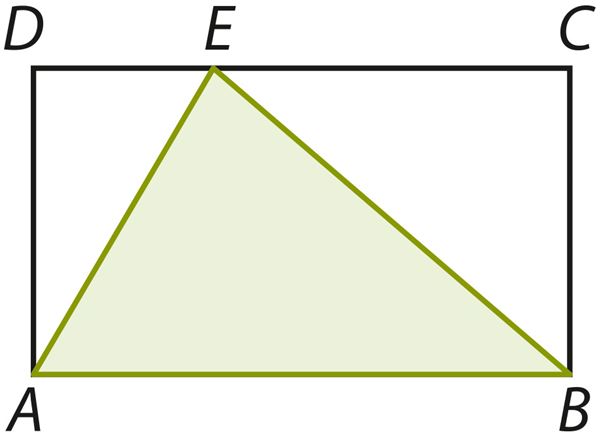
Ответ: площадь треугольника ABE равна см2. Результат от расположения вершины E на отрезке DC, так как .
Ответ: S = см2
Ответ: S = см2
Ответ: S = см2
Ответ: S = см2
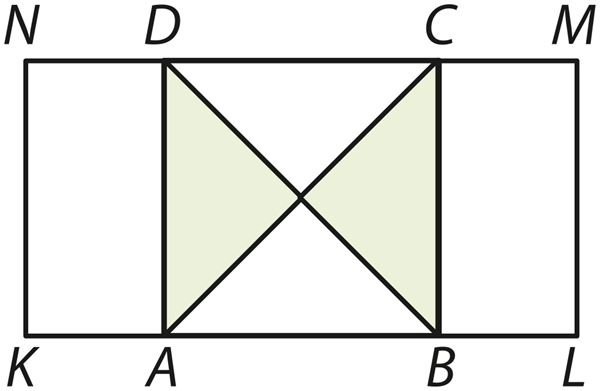
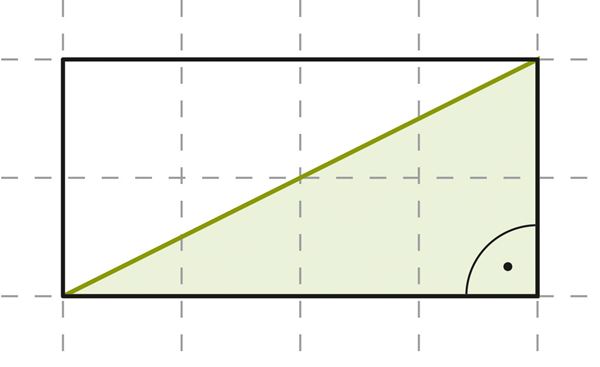
Ответ: площадь закрашенной части составляет% площади прямоугольника.
885.* Разбиение треугольника на равновеликие части
Начерти разносторонний треугольник и разбей его:
- с помощью прямой, проходящей через одну из вершин, на две части одинаковой площади;
- прямыми, проходящими через одну и ту же вершину, на четыре части с одинаковой площадью.
Обоснуй свое решение.
См. Приложение 12.
887. Программа GeoGebra
С помощью программы GeoGebra исследуй зависимость между площадью треугольника и площадью прямоугольника.
См. Приложение 13 и задание 881.
