Aritmeetiline keskmine, mediaan, mood

Statistiliste andmete kogumisele järgneb andmete töötlemine ehk andmeanalüüs. Selle käigus leitakse arvulised suurused, nn karakteristikud, mis iseloomustavad tunnuse väärtuste jaotust kui tervikut mingist seisukohast. Põhilised karakteristikud jagunevad kahte rühma: 1) paiknemise karakteristikud ehk keskmised ja 2) hajuvuse karakteristikud.

Paiknemise karakteristikud annavad informatsiooni tunnuse väärtuste paiknemise kohta arvteljel ja iseloomustavad tunnust keskmise väärtuse seisukohalt.

Hajuvuse karakteristikud näitavad, mil määral erinevad tunnuse väärtused üksteisest, hajuvad keskmise ümber.

Vaatleme järgnevalt paiknemise karakteristikuid. Need on aritmeetiline keskmine, mediaan ja mood.

Aritmeetiliseks keskmiseks nimetatakse tunnuse kõigi väärtuste summa ja kogumi mahu (objektide arvu) jagatist.

Aritmeetilist keskmist tähistatakse sümboliga \overline{x}. Arvutipõhisel andmetöötlusel esineb tähis AVERAGE või MEAN.Statistilise rea a₁, a₂, a₃, …, a_N korral on

\bar{x} = \frac{a_{1} + a_{2} + a_{3} + \dots + a_{N}}{N}

Kui andmestik on esitatud sagedustabelina

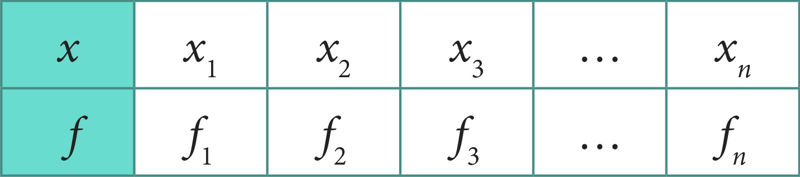
on aritmeetiline keskmine

$\bar{x} = \frac{x_{1} f_{1} + x_{2} f_{2} + \dots + x_{n} f_{n}}{N}$ .

Seda valemit nimetatakse ka kaalutud (aritmeetiliseks) keskmiseks, sest sagedused f_i näitavad, kui suur osakaal ehk kaal on tunnuse väärtusel x_i teiste väärtuste seas.

Kui andmestik on esitatud jaotustabelina

on $w_{i} = \frac{f_{i}}{N}$ korral aritmeetiline keskmine $\bar{x} = x_{1} w_{1} + x_{2} w_{2} + \dots + x_{n} w_{n}$ ,

$w_{i} = \frac{f_{i}}{N} \cdot 100 %$ korral $\bar{x} = \frac{x_{1} w_{1} + x_{2} w_{2} + \dots + x_{n} w_{n}}{100}$ .

Tõepoolest, w_i=\frac{f_i}{N} korral on \overline{x}=\frac{x_1f_1+x_2f_2+...+x_nf_n}{N} = x_1\frac{f_1}{N}+x_2\frac{f_2}{N}+...+x_n\frac{f_n}{N} = x_1w_1+x_2w_2+...+x_nw_n; analoogselt saame \overline{x} juhul w(%).

Näide 1. Peatüki 1.10. näite 2 klassi A andmetel on kontrolltöö hinnete aritmeetiline keskmine\overline{x} = \frac{2\cdot3+3\cdot7+4\cdot10+5\cdot8}{28} = \frac{107}{28} ≈ 3,82 ≈ 3,8. Sama töö hinnete aritmeetilise keskmise saame ka näite 3 esimese jaotustabeli andmetest (klass A):\overline{x} = \frac{2\cdot11+3\cdot25+4\cdot36+5\cdot28}{100} = \frac{381}{100} ≈ 3,8.

Kui statistiline andmestik on antud tabeliga, kus tunnuse väärtused on esitatud vahemikena, leitakse iga vahemiku esindaja, tavaliselt vahemiku x_i < x ≤ x_i+1 keskmine väärtus\frac{1}{2}\left(x_i+x_{i+1}\right),millega arvutatakse edasi nagu tunnuse üksikute väärtuste korral.

Näide 2. Leiame peatüki 1.10 näites 4 saadud tabeli andmetel õpilaste pikkuste aritmeetilise keskmise. Arvutused vormistame tabelina, mida on eriti otstarbekas teha (tasku)arvuti puudumisel.

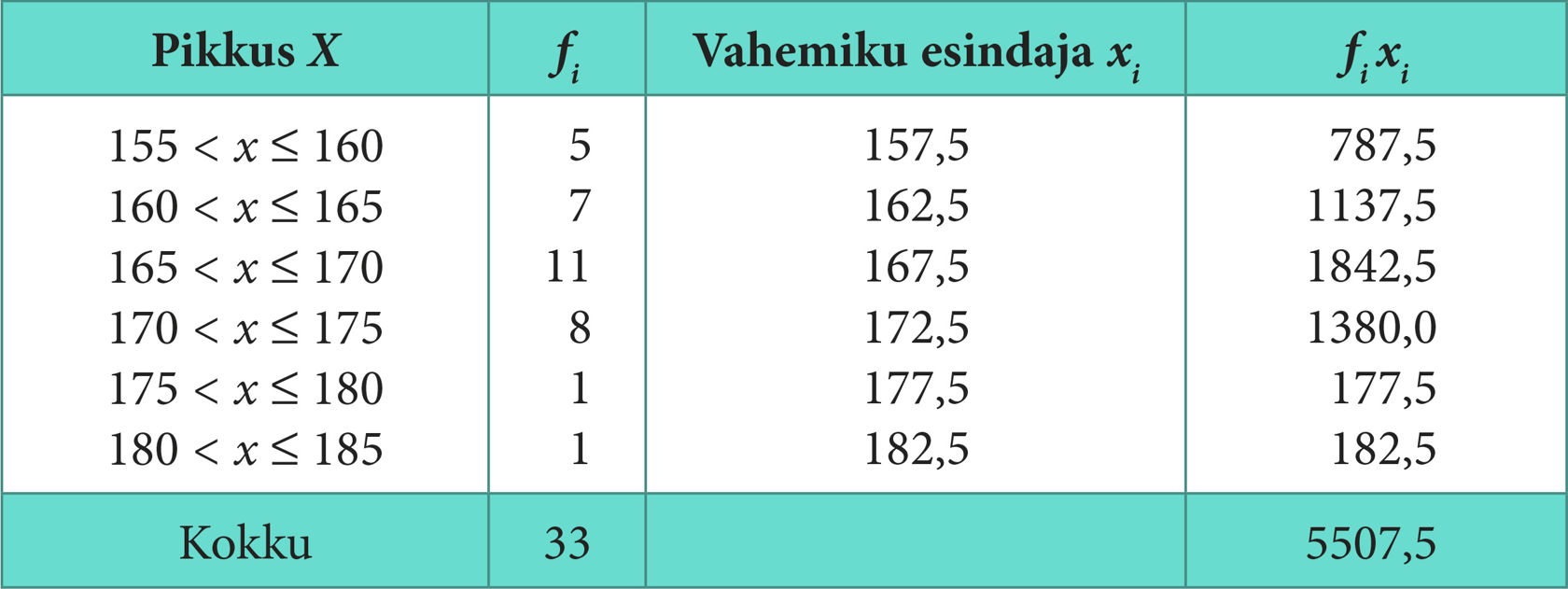
\overline{x}=\frac{5507,5}{33}\approx166,9

Vaadeldava klassi õpilaste keskmine pikkus on 166,9 cm.

Mediaaniks nimetatakse tunnuse väärtust, millest suuremaid (või võrdseid) ja väiksemaid (või võrdseid) liikmeid on variatsioonreas ühepalju.

Mediaani tähistatakse sümboliga Me või me, andmetöötlussüsteemides MEDIAN. Kui variatsioonreas on paaritu arv liikmeid (N on paaritu arv), on mediaaniks variatsioonrea keskmine liige. Kui aga variatsioonreas on paarisarv liikmeid, on mediaaniks kahe keskmise liikme aritmeetiline keskmine. Lühemalt:

$M e = x_{i}$ , kus $i = \frac{1}{2} (N + 1)$ kui N on paaritu arv,

$M e = \frac{1}{2} (x_{i} + x_{i + 1})$ , kus $i = \frac{N}{2}$ kui N on paarisarv.

Näide 3.

Ühe klassi noormeeste kinganumbrite variatsioonrida on 39, 39, 40, 40, 40, 40, 41, 41, 41, neiudel aga 35, 35, 35, 35, 36, 39. Leiame vastavad mediaanid.

Et esimesel juhul on N = 9, siis Me = x₅ = 40, sest keskmise liikme indeks i = 0,5(9 + 1) = 5. Neiude kinganumbrite variatsioonreas on paarisarv liikmeid (N = 6), seega Me = 0,5(x₃ + x₄) = 0,5(35 + 35) = 35.

Näide 4.

Järgnevas tabelis on esitatud kontrolltöö hinded. Leiame hinnete mediaani.

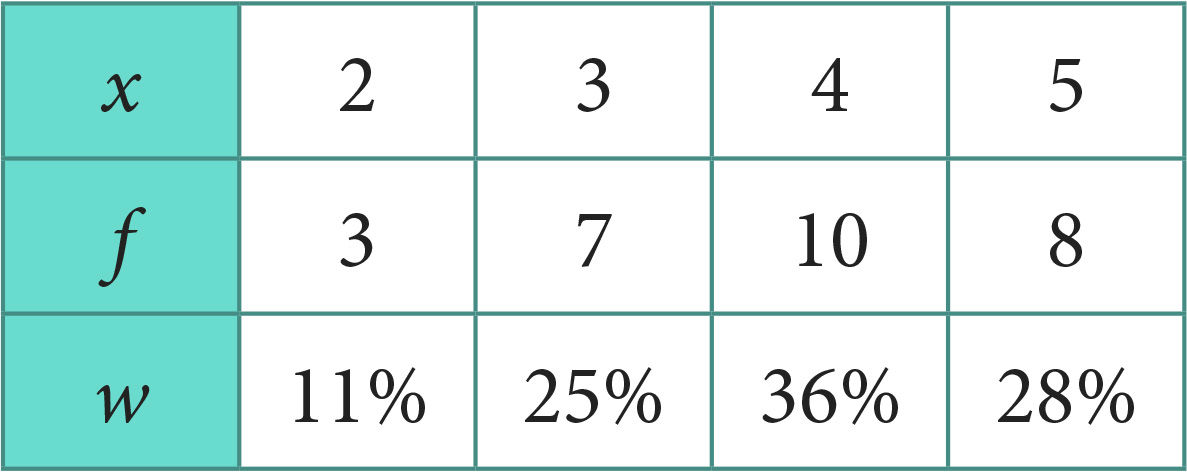Et hindeid on paarisarv ja N = 28, siis Me = 0,5(x₁₄ + x₁₅₎. Liites järjest sagedusi, saame, et x₁₄ = x₁₅ = 4. Järelikult Me = 4.

Suhteliste sageduste korral liidame järjest protsente ja vaatame, millise hinde korral saab summa suuremaks kui 50%: 11 + 25 = 36, kuid 11 + 25 + 36 > 50. Seega sai neljade lisamisel sageduste summa suuremaks kui 50% ja järelikult Me = 4.

Vahemikes esitatud sagedus- või jaotustabeli korral toimitakse nii nagu näites 4, aga tulemuseks saadakse nn mediaanvahemik. Näite 2 andmete korral on selleks vahemik 165 < x ≤ 170. Kui opereerida intervalli esindajaga, saame mediaaniks 167,5. Vastavast variatsioonreast (näide 4 peatükis 1.10) leiame, et Me = 167.

Kuigi aritmeetiline keskmine on keskmistest enamkasutatav, on juhtumeid, kus mediaan on sobivam. Nii on siis, kui variatsioonreas on üksikuid ebaharilikult suuri või väikseid väärtusi ja kogumi maht on väike. Nüüd nihkub aritmeetiline keskmine arvteljel kohta, kus tunnuse väärtusi tegelikult pole või on väga vähe. Mõningal määral ilmneb see ka näite 3 korral, kus neiude keskmine kinganumber \overline{x}=35,8\approx36, samal ajal kui enamik andmeid on 35-st 36-ni. Mediaan on aga 35, mis on keskmisena siin loomulikum.

Mediaani saab kergesti leida ja samas on ta hea aritmeetilise keskmise ligikaudseks hindamiseks. Mida sümmeetrilisem on tunnuse jaotus, seda paremini iseloomustab mediaan keskmist. Näiteks noormeeste kinganumbrite mediaan näites 3 on 40, aritmeetiline keskmine aga 40,1.

Mediaani saab sageli leida ka ühe või kahe mõõtmise teel. Leides näiteks õpilaste pikkuse mediaani, rivistame õpilased pikkuse järgi ja seejärel mõõdame vaid rea keskel asuva ühe või kahe õpilase pikkuse.

Moodiks nimetatakse tunnuse kõige sagedamini esinevat väärtust.

Moodi tähistatakse sümboliga Mo või mo, andmetöötlussüsteemides MODE. Kontrolltöö hinnete mood on näite 4 korral 4, sest sellele vastav sagedus on kõige suurem (f = 10 või w = 36%). Kui andmed on esitatud vahemikes, antakse kõige suurema sagedusega vahemik. Näite 2 korral on selleks vahemik 165 < x ≤ 170.

Tunnusel võib moode olla ka rohkem kui üks või tal võib ka mood puududa (kõigi väärtuste esinemise sagedus on sama). Kui moode on kaks, öeldakse, et tunnus (vaadeldav jaotus) on bimodaalne.

Kui jaotus on täiesti sümmeetriline ja sellel on üks mood, on \overline{x}=Me=Mo.

Moodi kasutatakse majanduses, kaubanduses, tarbija vajaduste uurimisel jne. Mõningatel juhtudel võib moodi vaadelda kui normi. Näiteks meeste soengu mood kui normaalne soeng, esmaabiellujate vanuse mood kui normaalne abiellumisaeg.

Ülesanded A

Ülesanne 158. Algaja laskuri tulemused

Vastus. Keskmine silmade arv ühe lasuga on .

Ülesanne 159. Kontrolltöö keskmine hinne

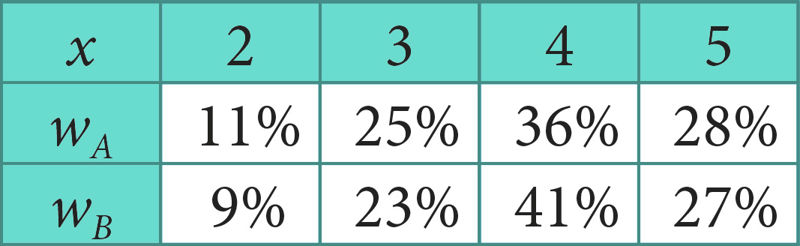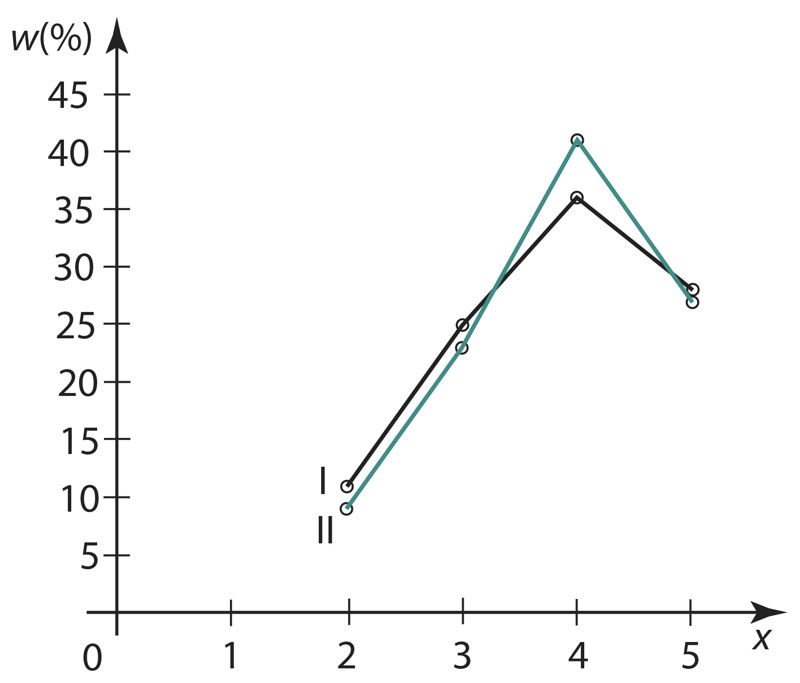Vastus. A klassi keskmine hinne on ja B klassi keskmine hinne on . Järelikult

Ülesanne 160. Neidude ja noormeeste keskmine pikkus

Ülesanne 161. Õpilaste pikkuste aritmeetiline keskmine

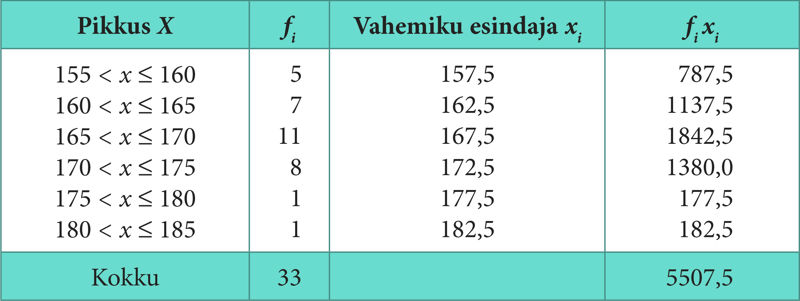
\overline{x}=\frac{5507,5}{33}\approx166,9

Koostage antud tabeli põhjal uus sagedustabel, kus klasse on vaid kolm. Arvutage nüüd õpilaste pikkuste aritmeetiline keskmine ja võrrelge seda eelneva tulemusega.

Pikkus X	f_i	Vahemiku esindaja x_i	f_ix_i
< x ≤
< x ≤
< x ≤
Kokku

\overline{x}\approx

Ülesanne 162. Kinganumbrite mediaan

Vastus. Müüdud kingade numbrite mediaan on .

Ülesanne 163. Neidude ja noormeeste jalatsinumbrite mediaan

Ülesanne 164. Meeste ja naiste vanuse mediaanvahemik ja kõige sagedamini esinev vanusevahemik

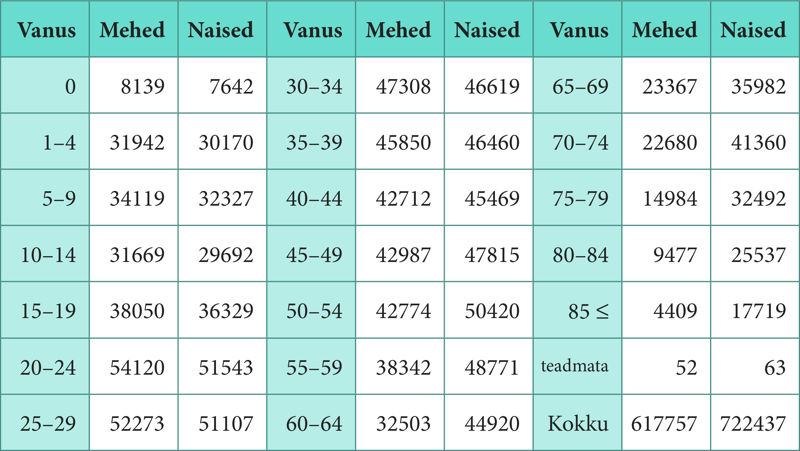
Milline on Eestis 2011. aasta andmetel meeste ja naiste vanuse mediaanvahemik ja kõige sagedamini esinev vanusevahemik?

Vastus. Mediaanvahemik oli meestel ja naistel aastat. Kõige sagedamine esinev vanusevahemik oli meestel ja naistel aastat.

Ülesanne 165. Jaotus sünnikuude järgi

Vastus. Kõige vähem lapsi sündis ( last) ja kõige rohkem ( last). Nende laste arvude erinevus on last. Keskmine laste sündimise protsent on %, s.o last.

Ülesanne 166. Jaotustabel sünnikuu järgi

Vastus. Mo =

Ülesanne 167. Algaja laskuri tulemused

Me =

Mo = ja

\overline{x} =

Ülesanne 168. Täis- ja kaashäälikute arv eestikeelses tekstis

Vastus. Mo =

Ülesanne 169. Eesti rahvuslik koosseis

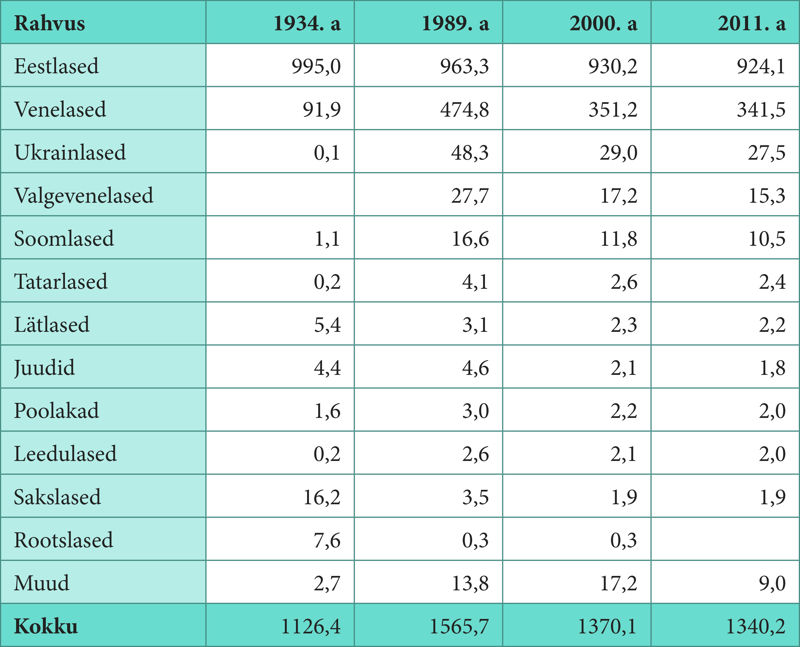
Vastus. Mo =

Ülesanne 170. India elevantide keskmine mass

Vastus. India elevantide keskmine mass on kg.

Ülesanne 171. Elevantide massid viie vahemikuna

Vastus. India elevantide massi mediaanvahemik on , suurima sagedusega vahemik on ja massi aritmeetiline keskmine on .

Ülesanne 172. Matemaatika kontrolltöö keskmine hinne, mediaan ja mood

Leidke oma klassi viimase matemaatika kontrolltöö hinnete \overline{x}, Me ja Mo (võite kasutada ülesande 152 andmeid). Andke kontrolltöö tulemustele omapoolne hinnang.

Vastus. \overline{x} = , Me = , Mo = .

Hinnang:

Ülesanne 173. Kahe klassi keskmine hinne

Vastus. Kahe klassi peale kokku on vaadeldava töö keskmine hinne .

Aritmeetiline keskmine, mediaan, mood

More like this

Ülesanded A

Ülesanne 158. Algaja laskuri tulemused

Ülesanne 159. Kontrolltöö keskmine hinne

Ülesanne 160. Neidude ja noormeeste keskmine pikkus

Ülesanne 161. Õpilaste pikkuste aritmeetiline keskmine

Ülesanne 162. Kinganumbrite mediaan

Ülesanne 163. Neidude ja noormeeste jalatsinumbrite mediaan

Ülesanne 164. Meeste ja naiste vanuse mediaanvahemik ja kõige sagedamini esinev vanusevahemik

Ülesanne 165. Jaotus sünnikuude järgi

Ülesanne 166. Jaotustabel sünnikuu järgi

Ülesanne 167. Algaja laskuri tulemused

Ülesanne 168. Täis- ja kaashäälikute arv eestikeelses tekstis

Ülesanne 169. Eesti rahvuslik koosseis

Ülesanne 170. India elevantide keskmine mass

Ülesanne 171. Elevantide massid viie vahemikuna

Ülesanne 172. Matemaatika kontrolltöö keskmine hinne, mediaan ja mood

Ülesanne 173. Kahe klassi keskmine hinne

More like this

Opiq score

	Tasks
	Chapter is studied

Aritmeetiline keskmine, mediaan, mood

More like this

Ülesanded A

Ülesanne 158. Algaja laskuri tulemused

Ülesanne 159. Kontroll­töö keskmine hinne

Ülesanne 160. Neidude ja noor­meeste keskmine pikkus

Ülesanne 161. Õpilaste pikkuste aritmeetiline keskmine

Ülesanne 162. Kinga­numbrite mediaan

Ülesanne 163. Neidude ja noor­meeste jalatsi­numbrite mediaan

Ülesanne 164. Meeste ja naiste vanuse mediaan­vahemik ja kõige sagedamini esinev vanuse­vahemik

Ülesanne 165. Jaotus sünni­kuude järgi

Ülesanne 166. Jaotus­tabel sünni­kuu järgi

Ülesanne 167. Algaja laskuri tulemused

Ülesanne 168. Täis- ja kaas­häälikute arv eesti­keelses tekstis

Ülesanne 169. Eesti rahvuslik koosseis

Ülesanne 170. India elevantide keskmine mass

Ülesanne 171. Elevantide massid viie vahemikuna

Ülesanne 172. Matemaatika kontrolltöö keskmine hinne, mediaan ja mood

Ülesanne 173. Kahe klassi keskmine hinne

More like this

Add content

Files to be added

Report Mistake

Only report errors related to the functionality or content of Opiq. Please describe the error as precisely as possible.

If you agree to share additional info, add your contact data (e-mail, phone).

Check to help us fight spam

Opiq uses cookies

Ülesanne 159. Kontrolltöö keskmine hinne

Ülesanne 160. Neidude ja noormeeste keskmine pikkus

Ülesanne 162. Kinganumbrite mediaan

Ülesanne 163. Neidude ja noormeeste jalatsinumbrite mediaan

Ülesanne 164. Meeste ja naiste vanuse mediaanvahemik ja kõige sagedamini esinev vanusevahemik

Ülesanne 165. Jaotus sünnikuude järgi

Ülesanne 166. Jaotustabel sünnikuu järgi

Ülesanne 168. Täis- ja kaashäälikute arv eestikeelses tekstis