Курс "Функции"
Пример 1.
Пусть в банк поместили начальный капитал в размере 10 евро, и банк выплачивает 9% годового инресса. Тогда в конце n-го года на счете в банке будет
Построим ее график с помощью таблицы значений функции.
Отметим на координатной плоскости точки, соответствующие парам чисел n и у. Получим график, изображенный на рисунке 2.37. Отдельные точки не нужно соединять плавной линией, так как аргумент n принимает только натуральные значения.
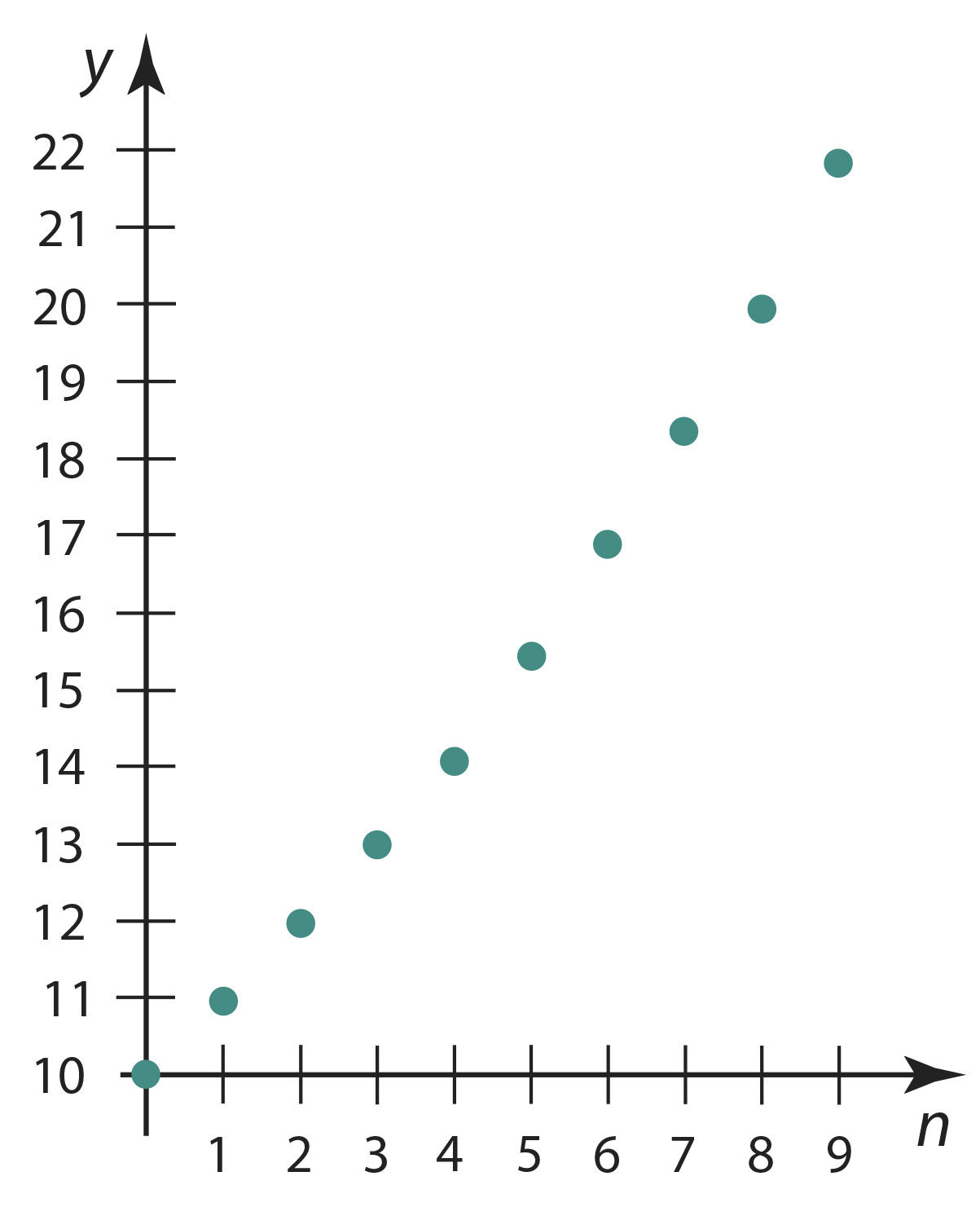 Рис. 2.37 | ||||||
Если в примере 1 взять вместо коэффициента 10 некоторое число с, обозначить выражение в скобках через а, где а > 0 и а ≠ 1, и заменить показатель степени n на произвольную действительную переменную х, то мы получим все возможные значения такой функции. Эта новая функция определяется так.
Функция y = cax, где a > 0, a ≠ 1, x ∈ R, называется показательной функцией[понятие: Показательная функция (eksponentfunktsioon) – функция 𝑦 = 𝑐𝑎ˣ, где 𝑎 > 0 , 𝑎 ≠ 1 и 𝑐 – некоторое отличное от нуля число, чаще всего 𝑐 = 1.]. Показательную функцию называют также экспонентой[cноска: От латинского слова exponere – выставлять, показывать.].
Если исходить из убывания некоторой величины по закону показательного убывания (например, количества радиоактивного вещества, численности населения города), то, обобщив формулу
Пример 2.
Функции y = 2x, y = 0,6x, y = 2,34x и y = 5 · 0,9x являются показательными функциями.
Пример 3.
Пусть показательная функция y = 100 · 1,025x описывает увеличение банковского вклада в течение х лет, т. е. x ∈ N. Какова была первоначально помещенная в банк сумма? Сколько процентов интресса в год выплачивает банк? Какая сумма будет на счете через 8 лет?
В банк поместили c = 100 евро. Так как основание степени
Далее мы будем рассматривать в основном показательные функции вида y = ax.
Областью определения показательной функции является множество R всех действительных чисел, т. е. X = R, или –∞ < x < +∞.
Рассмотрим свойства показательной функции y = ax.
1. Областью положительности показательной функции является вся область ее определения (X+ = R), область отрицательности отсутствует.
В самом деле, при a > 0 степень ax с любым действительным показателем х всегда положительна.
2. Показательная функция не имеет нулей.
Это свойство следует из предыдущего.
3. График показательной функции проходит через точку A(0; 1).
Действительно, если x = 0, то y = a0 = 1.
4. График показательной функции проходит через точку B(1; a).
Действительно, если x = 1, то y = a1 = a.
5. Если a > 1, то показательная функция является возрастающей, X↑ = R;
если 0 < a < 1, то показательная функция является убывающей, X↓ = R.
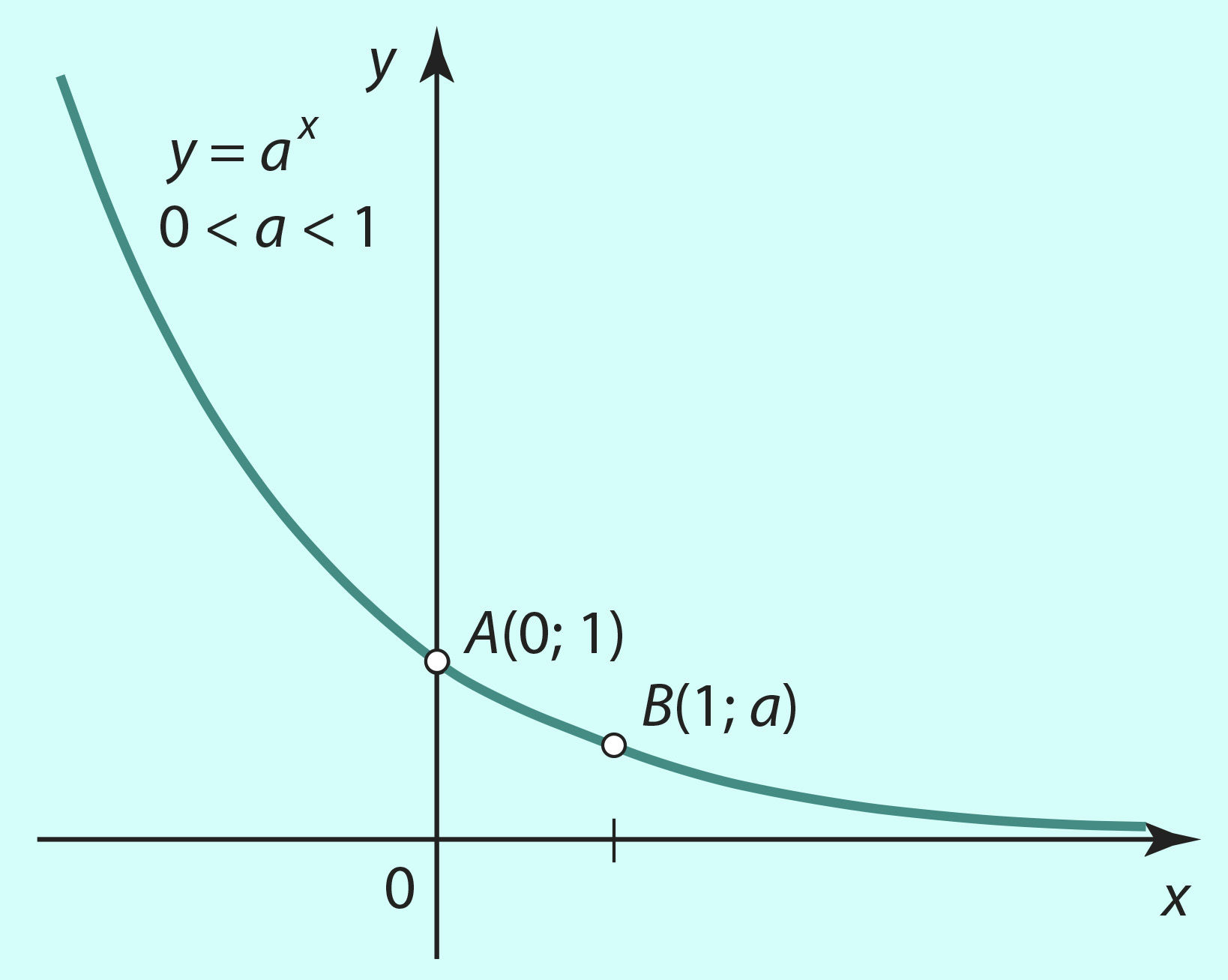
Графики показательной функции y = ax изображены на рисунке 2.38 (случай а > 1) и на рисунке 2.39 (0 < a < 1).
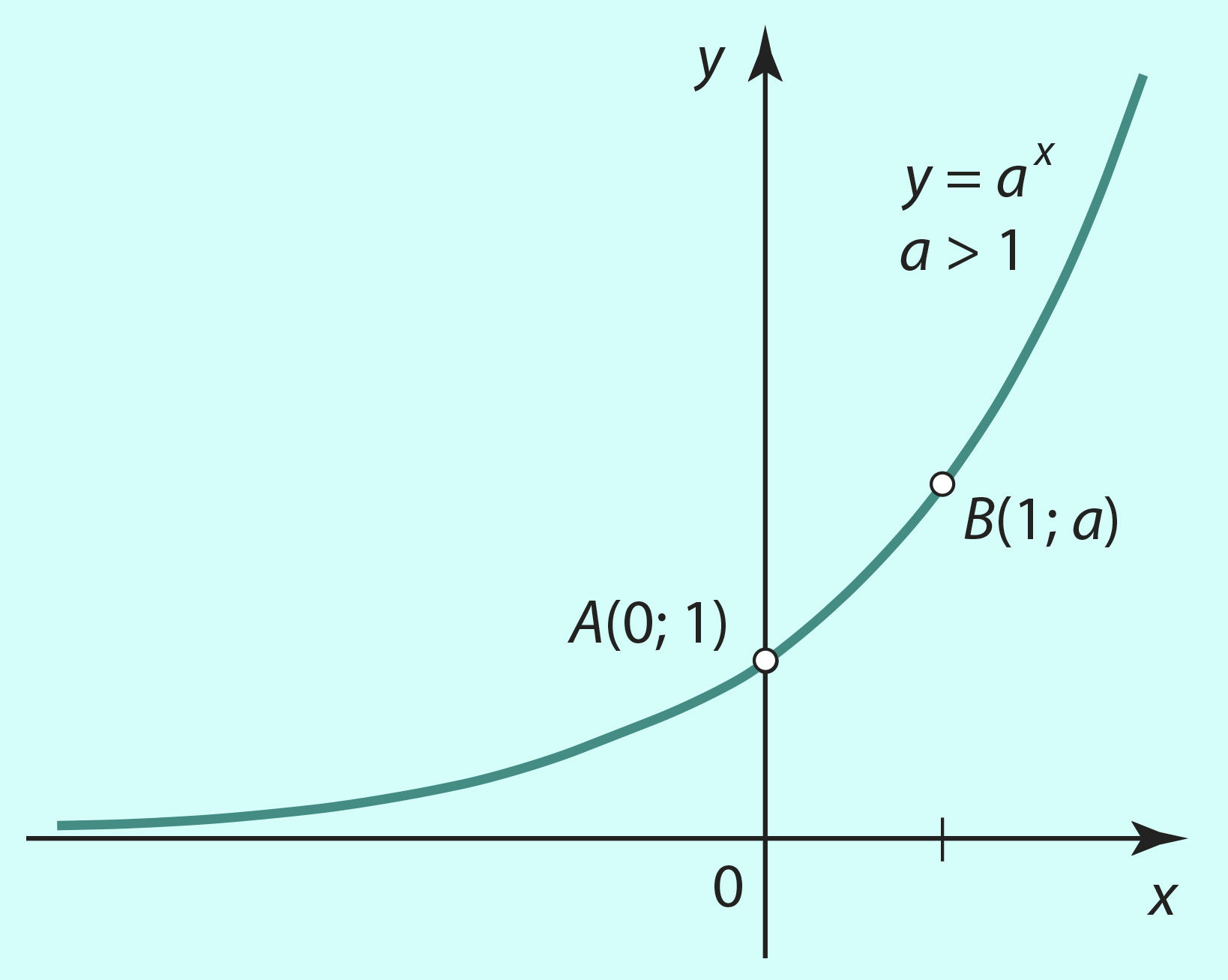
На рисунке 2.38 видно, что
если a > 1, то при неограниченном увеличении аргумента x (x ∈ R, x → ∞) значения функции y = ax также неограниченно увеличиваются (y → ∞).
А для изображенного на рисунке 2.39 случая 0 < a < 1:
если 0 < a < 1, то при неограниченном увеличении аргумента x (x → ∞) соответствующие значения функции y = ax уменьшаются, неограниченно приближаясь к нулю (y → 0).
На рисунке 2.38, если двигаться справа налево: если a > 1, то при неограниченном уменьшении аргумента x ∈ R (т. е. когда x → –∞), значения функции у = ax неограниченно приближаются к нулю (y → 0).
Пример 4.
Если y = 5x, то придавая аргументу х все меньшие (в том числе и отрицательные) значения, мы получаем все меньшие значения функции: при x = 2; x = –3; x = –8 получим соответственно, что у = 25; у = 0,008; у = 0,000 002 56.
Прямую, к которой неограниченно приближается некоторая линия (например, график функции) при неограниченном удалении от начала координат, называют асимптотой[cноска: От греческого слова асюмптотос – не совпадающий.] этой линии (графика). Асимптотой графика функции y = ax для обоих случаев a > 1 и 0 < a < 1 является ось абсцисс.
Областью определения показательной функции y = ax является множество всех действительных чисел, т. е. X = R, а множеством значений множество всех положительных действительных чисел, т. е. Y = R+.
Пример 5.
Построим графики функций
Отметим на координатной плоскости соответствующие точки (x; f(x)) и соединим эти точки плавной непрерывной линией (рис. 2.40 и 2.41).
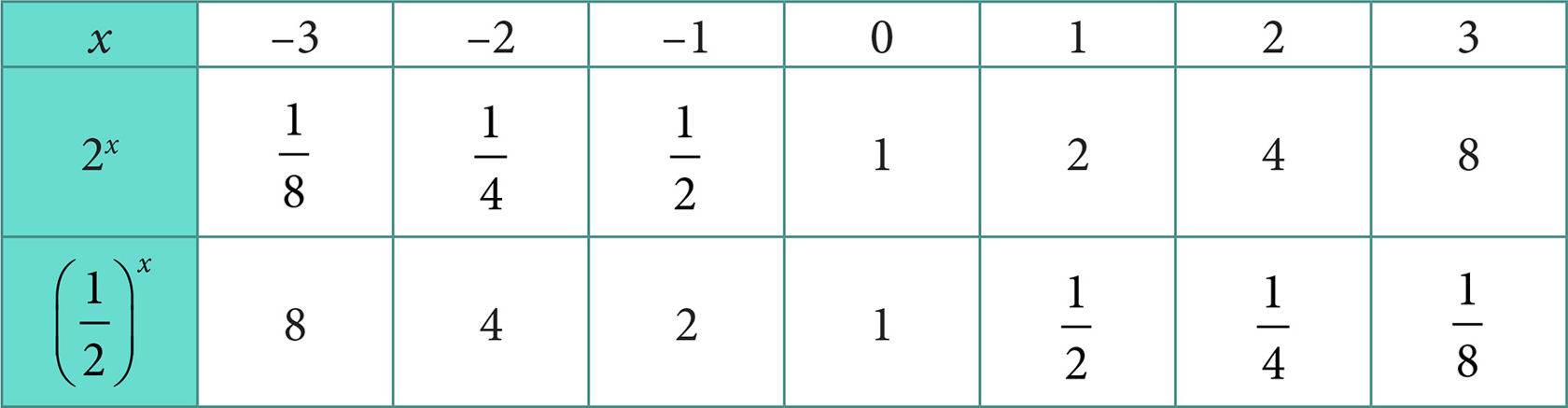
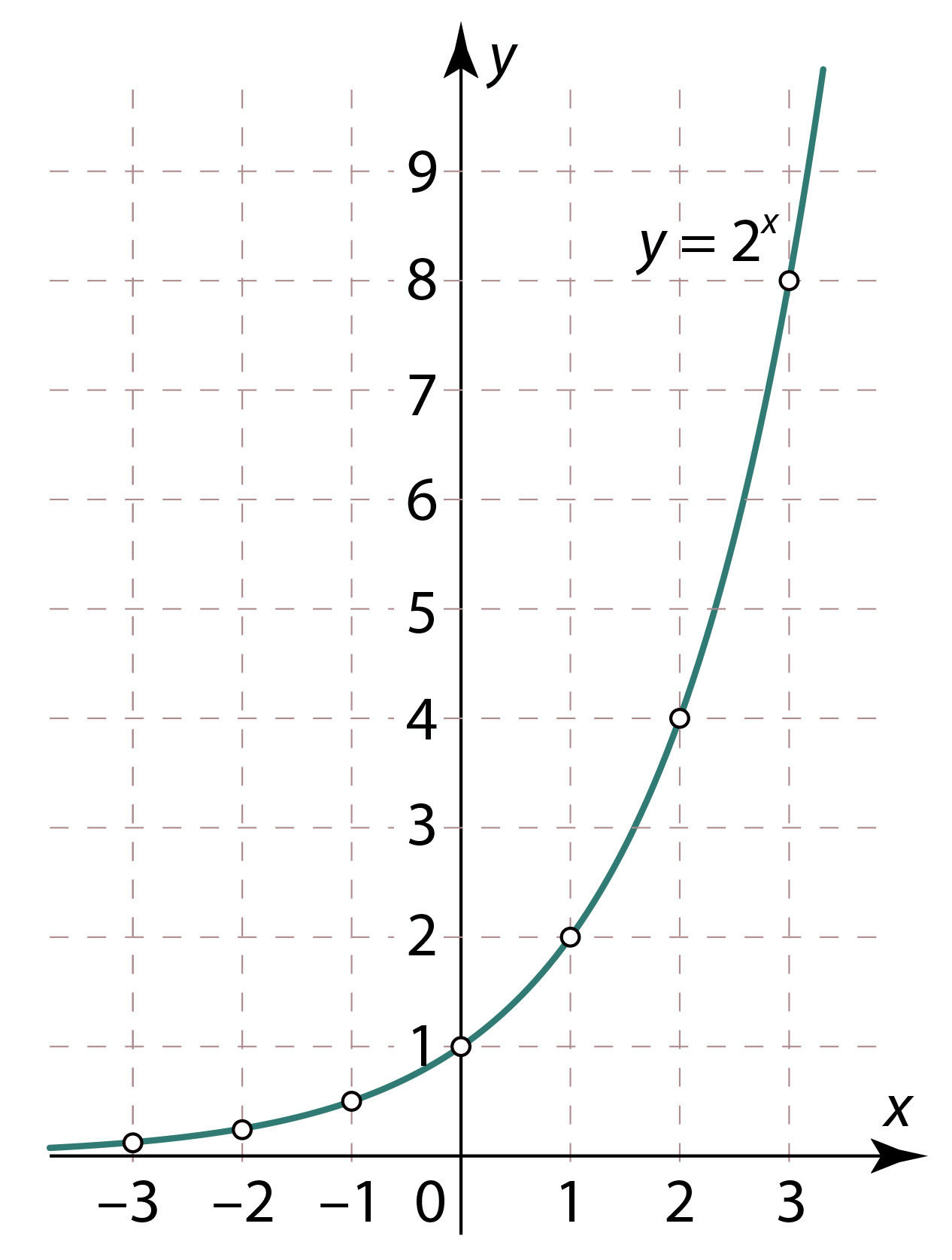 Рис. 2.40 | ||||||
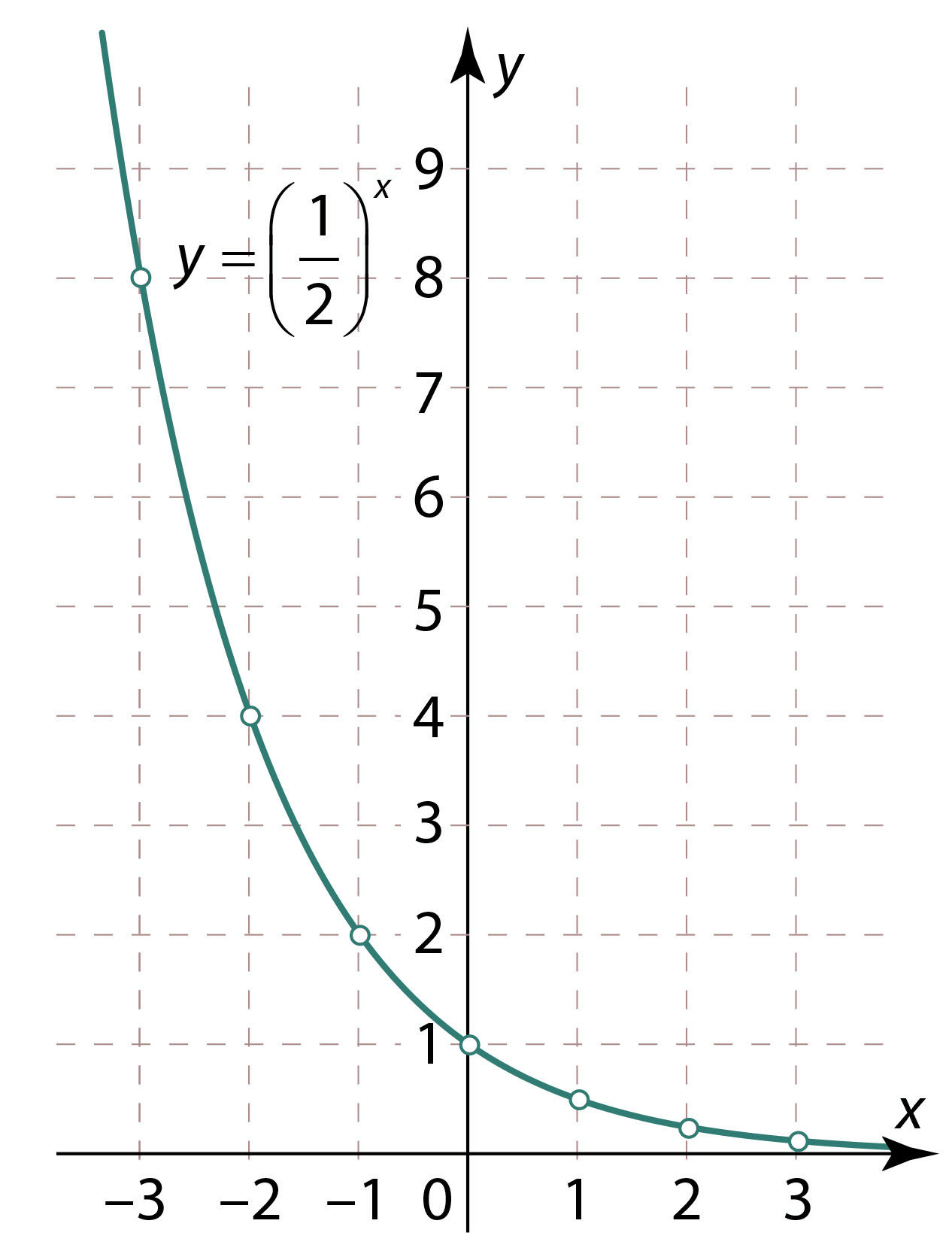 Рис. 2.41 | ||||||
Рассмотренный пример позволяет сказать, что
графики показательных функций и симметричны друг другу относительно оси ординат.
На рисунках 2.42 и 2.43 показано, как влияет увеличение основания а на форму графика функции y = ax при a > 1 (рис. 2.42) и при 0 < a < 1 (рис. 2.43).
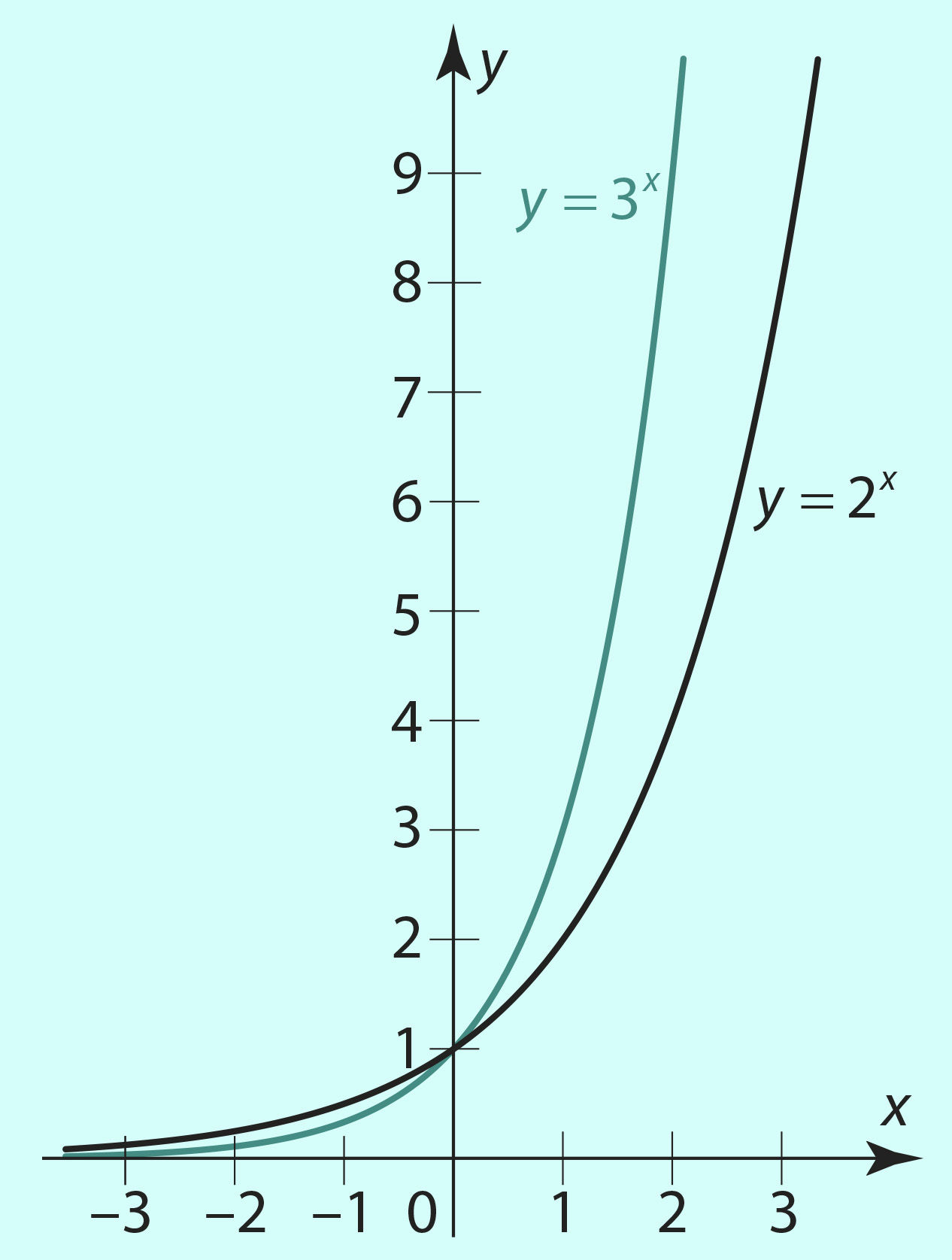 Рис. 2.42 | ||||||
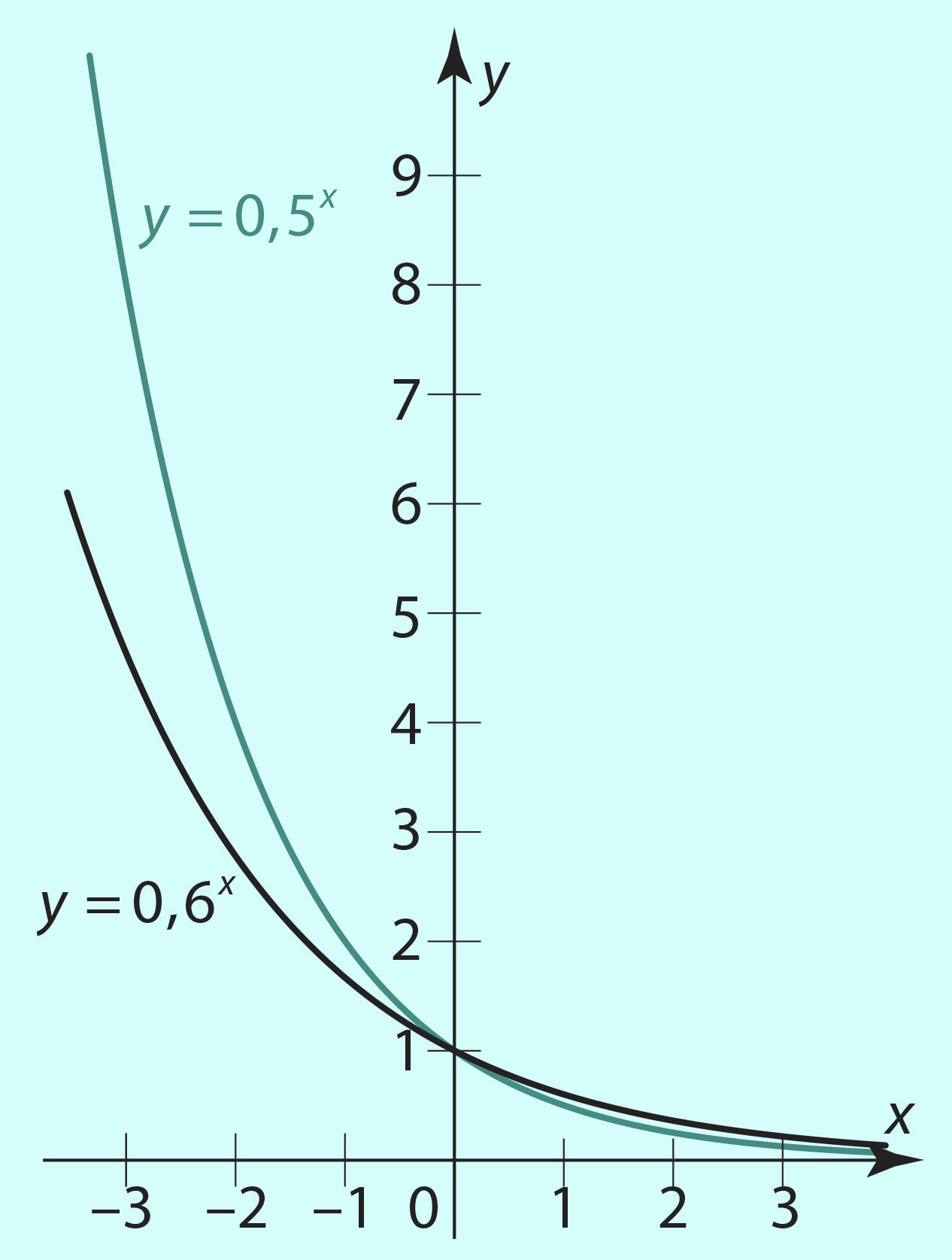 Рис. 2.43 | ||||||
Пример 6.
С помощью рисунков 2.40 и 2.41 найдем для функций
Для обеих функций X = R, Y = R+, X+ = R и X– = ∅. Функция y = 2x является возрастающей, т. е. X↑ = R и X↓ = ∅. Функция
Если возрастание или убывание некоторой величины y задается равенством y = ax, то говорят, что возрастание (a > 1) или убывание (0 < a < 1) этой величины происходит по закону показательного роста[понятие: Закон показательного роста (eksponentsiaalne kasvamine) – возрастание величины 𝑦 по закономерности 𝑦 = 𝑎ˣ, где 𝑎 > 1.] (или убывания[понятие: Закон показательного убывания (eksponentsiaalne kahanemine) – убывание величины 𝑦 по закономерности 𝑦 = 𝑎ˣ, где 0 < 𝑎 < 1.]). Этот закон называют также экспоненциальным законом (роста или убывания).
Упражнения
Постройте в одной и той же системе координат графики функций
Каковы у этих функций их области определения, области положительности и отрицательности, интервалы возрастания и убывания? Есть ли у них точки экстремума?
Постройте в одной и той же системе координат графики функций
Какая сумма была помещена в банк? | Сколько процентов годового интресса выплачивает банк? | Какая сумма будет на счете через 10 лет? | |
y = 800 · 1,03x | € | % | |
y = 1200 · 1,02x | € | % | |
y = 1,1x | € | % | |
y = 10 500 · 1,006x | € | % |
Ответ: если на цилиндре 0,5 витка, то уравновесить груз можно силой в Н; если на цилиндре 1 виток, то Н; если на цилиндре 1,25 витка, то Н; если 2 витка, то Н; если 3 витка, то Н.
Ответ: если на цилиндре будет 1 виток, то уравновесить груз можно силой в Н; если на цилиндре 1,5 витка, то Н; если 2 витка, то Н; если 3 витка, то Н; если 4 витка, то Н; если 5 витков, то Н.
Ответ: через 2 часа будет получено кг дрожжей; через 3,5 часа – кг; через 6 часов – кг; через 8 часов – кг; через 9 часов – кг.
- Постройте график описывающей рост дрожжей функции p = 90 · 1,2t в промежутке между 0 и 9 часами.
- через 5 минут?
Ответ: через 5 минут температура кофе будет °. - через 15 минут?
Ответ: через 15 минут температура кофе будет °.
Через сколько минут она станет равной 15°?
Какая прямая является асимптотой графика рассматриваемой функции?
Ответ: прямая y = .
Ответ: Лиза получила кофе температурой в °.
