Курс „Последовательности. Производная функции”
Автомобиль движется вдоль пути, изображенного на рисунке 3.13, начиная от точки О, от которой измеряется расстояние (начало отсчета) и затраченное на путь время. Функция, позволяющая в каждый момент времени t вычислить расстояние s, пройденное телом (автомобилем и т. п.) вдоль некоторого пути (линии) начиная от начальной точки О, называется законом движения[понятие: Закон движения (liikumisseadus) – функция, выражающая расстояние 𝑠 от движущейся точки до начала отсчета (некоторой точки 𝑂) в любой момент времени 𝑡.] тела (или точки).
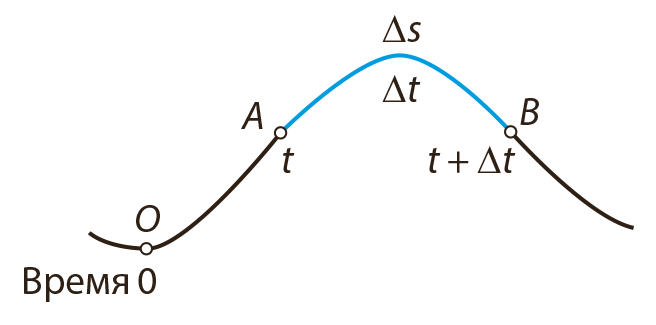
Пусть закон движения автомобиля на рисунке 3.13 выражается функцией
Поскольку пройденные к этим моментам пути соответственно
Соответствующая средняя скорость[понятие: Средняя скорость (keskmine kiirus) – отношение Δ𝑠 :Δ𝑡. Соответствует промежутку между 𝑡 и 𝑡 + Δ𝑡.] в промежутке времени [t; t + ∆t] (или на отрезке АВ) была
Найдем теперь, какова была скорость движения объекта в точке А, т. е. в момент времени t. Эта скорость называется мгновенной скоростью[понятие: Мгновенная скорость (hetkkiirus) – предел средней скорости движения когда приращение аргумента (времени) стремится к нулю.] и обозначается v. Она характеризуется средней скоростью vср тем точнее, чем меньше ∆s или, другими словами, чем короче длина ∆t промежутка времени. Следовательно,
если
Так как закон движения является функцией
, или
Пример.
Убедимся, что в случае закона свободного падения
Если
Тогда по определению мгновенной скорости получим, что если
Найденное соотношение
