Kuidas teadlased uurivad nähtusi

Füüsikat on arendanud teadlased, inimesed, kes on harjumuspärases looduse toimimises märganud midagi ebaharilikku, seda uurinud ja andnud uuritavale nähtusele seletuse.

Nüüdisaegse loodusteadusliku uurimismeetodi rajajaks loetakse Galileo Galileid (1564–1642). Galilei leidis, et loodusteaduslik uurimine peab põhinema katsel (eksperimendil), mis on teaduses peamiseks tõe allikaks. Katses on oluline mõõtmine ja kindlate ühikute kasutamine. Katse tulemused tuleb formuleerida mate­maatiliselt, teisisõnu, loodusteadused on matemaatilised. Loodusteadused tuleb eraldada filosoofiast ja religioonist.

Galilei tõestas, et nn Aristotelese füüsika, mille põhitõdedesse usuti ligi kaks aastatuhandet, ei kehti. Nii tõestas Galilei katseliselt, et vaba keha on kas paigal või liigub ühtlaselt ja sirgjooneliselt. Samuti tõestas ta, et vabalt langevad kehad langevad ühte moodi. Aristotelese arvates pidid suurema massiga kehad langema kiiremini väiksema massiga kehadest. Kui Aristoteles arvas, et Kuu on sile peegeldava pinnaga sfääriline taevakeha, siis Galilei vaatlused pikksilmaga tõestasid, et Kuul on mäed ja kraatrid, mille tõttu ta peegeldab päikesevalgust praktiliselt ühtlaselt.

Kui enne Galileid arendasid ideed, et tõese teadmise allikas on katse, araabia teadlane Alhazen (965–1040) ja tema eeskujul inglise teadlane Roger Bacon (1214–1294), siis praktikas viis selle idee ellu alles Galileo Galilei.

Nüüdisajal on võrdväärselt tähtsad nii katselised kui ka teoreetilised uurimused. Katselistel uurimustel tuleb alati arvestada uuritavate nähtustega seotud teoreetilisi ettekujutusi, mis on leidnud juba eelnevalt kinnitust.

Järgneval skeemil on esitatud üldpilt loodusteadusliku uurimismeetodi etappidest ja nende järgnevusest.

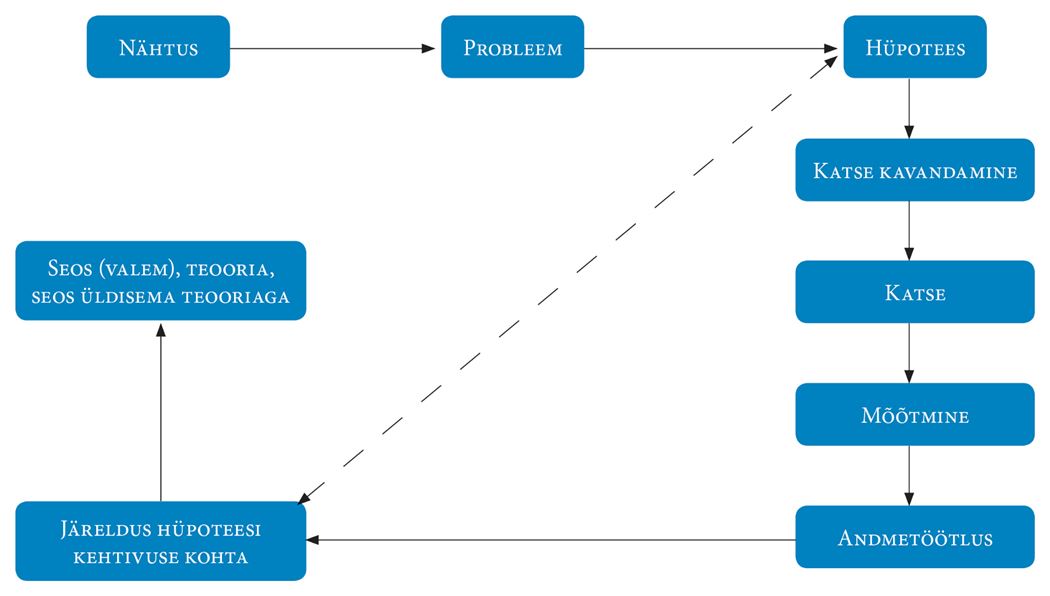
Teooria on matemaatiline mudel, millega me püüame seletada füüsikanähtusi, tuletades neid järeldusena juba tuntud nähtustest. Näiteks rääkides kehade soojuspaisumisest me lähtume aineosakeste soojusliikumisest. Mida kõrgem on temperatuur, seda intensiivsemalt aineosakesed liiguvad ja seda suuremaks muutuvad aineosakeste vahed.

Füüsikanähtuste kirjeldamisel me kasutame oskussõnu ehk termineid. Neil on täpne tähendus, mis antakse definitsiooniga. Soojuspaisumise korral on nendeks aine­osake, soojusliikumine ja temperatuur. Õpikus kasutatavate oskussõnade selgitusi leiad õpiku lõpus olevast sõnastikust.

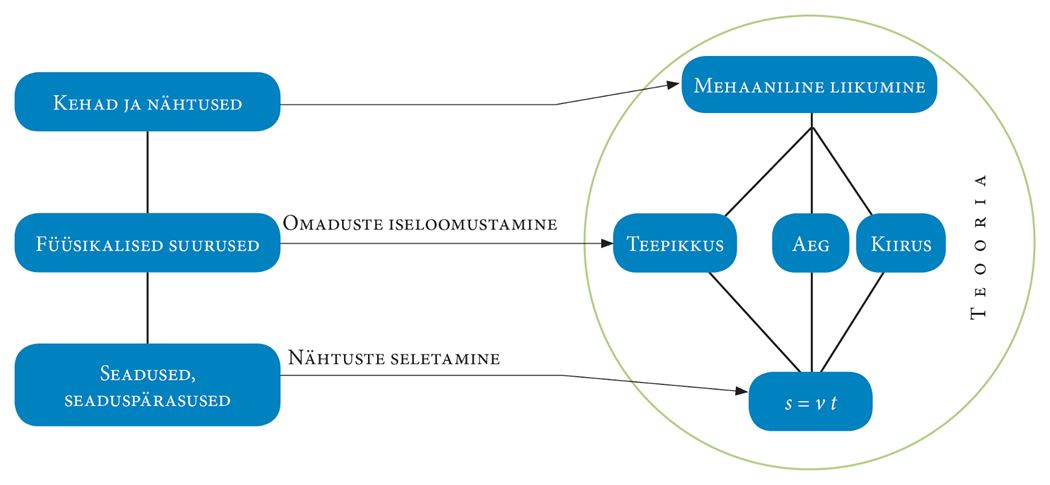
Igas teoorias on alati kolm osapoolt:

1. kehad ja nähtused;
2. füüsikalised suurused;
3. seadused või seaduspärasused.

Vaata skeemi!

Füüsika seadused on matemaatilised. Piltlikult öeldes on matemaatika keel, milles on kirja pandud loodusseadused. Erinevus matemaatikast on aga selles, et igal füüsikalisel suurusel on lisaks tema arvväärtusele alati kindel mõõtühik, mida tuleb selle suurusega opereerimisel teada. Füüsikaliste suurustega sooritatakse matemaatilisi tehteid: samanimelisi suurusi liidetakse või lahutatakse, erinimeliste füüsikaliste suuruste korrutamisel või jagamisel saadakse uusi füüsikalisi suurusi.

Füüsikanähtused on enamasti omavahel põhjuslikult seotud, üks nähtus põhjustab paljudel juhtudel teise. Füüsika seadused väljendavad nähtuses põhjuse ja taga­järje seost. Siin on samuti erinevus füüsika ja matemaatika vahel. Matemaatikas käsitletakse sõltumatut ja sõltuvat muutujat, kusjuures see sõltub meie valikust, s.t vaadeldava funktsiooni kujust. Nii näiteks funktsiooni y = 5x korral loeme suurust x sõltumatuks muutujaks, andes talle ette suvalisi arvväärtusi, nende kaudu arvutatud funktsiooni väärtust y loeme sõltuvaks muutujaks. Füüsikas on sõltumatuks muutujaks alati see suurus, mis kirjeldab nähtuse muutumise põhjust, sõltuvaks muutujaks aga suurus, mis kirjeldab seda, milline on nähtuse edasine kulgemine ehk tagajärg. Arvutades ühtlasel liikumisel läbitud teepikkuse sõltuvust ajast s = vt on sõltumatuks muutujaks aeg t, sõltuvaks muutujaks läbitud teepikkus s. Funktsioon on sama kujuga (võrdeline sõltuvus), erinevus aga selles, et teepikkuse arvutamise valemis on kindla ühikuga füüsikalised suurused (läbitud teepikkus, kiirus, aeg). See tähendab, et me peame teadma nendele suurustele vastavaid ühikuid ja oskama neid õigesti kasutada. Kui näiteks kiirus on antud kilomeetrites tunnis, siis peame andma aja tundides, et saada läbitud teepikkust kilomeetrites. Kui me aga tahame aega anda sekundites, peame kiiruse teisendama meetriteks sekundis ja tulemuseks saame läbitud teepikkuse meetrites.