Võnkumine

Miku vanavanematel on pendelkell. Niikaua kui Mikk mäletas, on selline kell neil alati olnud. Juba väiksena meeldis Mikule kellapendli võnkumist vaadata. Mõnikord, kui und ei tulnud, luges ta kaasa pendli võnkumisi.

Suuremaks saades tekkis Mikul küsimus, kuidas on pendli võnkumine ja kella ajanäitamine seotud.

Loe sissejuhatusest lugu lühtri võnkumise kohta. Galilei sai lühtri võnkumist üksnes vaadelda, katsetada lühtriga ei saanud. Nähtuse uurimiseks aga on vaja teha katseid. Teatud omadustelt peab katsevahend olema lühtri sarnane. Lühter on raske ja ripub pika varre otsas. Vars on lühtrist palju kergem. Katsetamiseks sobib keha, mis on riputatud varda või niidi otsa. Sellist süsteemi nimetatakse pendliks.

Järgnevalt vaatame niitpendli võnkumisi. Niitpendel on lihtsaim ja kergesti valmistatav pendel, mistõttu sellega on kõige lihtsam võnkumisi uurida. Niitpendli korral eeldame, et koormis on riputatud venimatu niidi otsa. Selline pendel mudeldab ka lühtri võnkumisi.

Võnkumine kuulub korrapäraste, teatud aja jooksul korduvate liikumiste hulka. Võnkuvaid kehi on väga palju. Vette langenud puuleht liigub koos veega üles-alla, vedru otsa riputatud koormis liigub vedru tasakaaluasendist välja viies üles-alla, aineosakesed võnguvad tahkes aines soojusliikumise tõttu oma tasakaaluasendi ümber jne. Järgnevalt uurime pendli võnkumisi ja sellega seotud peamisi füüsikalisi suurusi.

Vaatame pendli liikumist lähemalt.

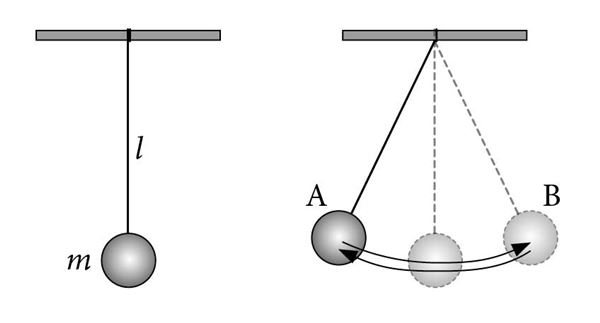
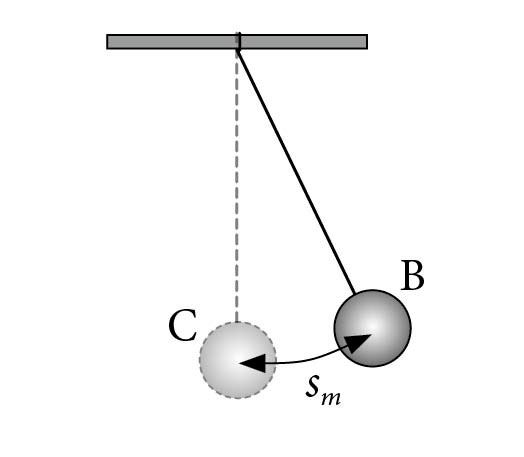
Pendlil on kindel tasakaaluasend. See on asend, kus koormis ripub vertikaalselt niidi otsas. Selles asendis olev pendel on paigal ja ise, ilma välise mõjuta liikuma ei hakka. Viime nüüd koormise tasakaaluasendist välja (asend A, niit on vertikaalsihiga mingi nurga all) ja laseme lahti. Koormise kiirus hakkab suurenema ja saadud hooga läbib ta tasa­kaaluasendi. Edasi hakkab kiirus kahanema ja koormis jõuab teise äärmisse asendisse (asend B), mis on tasakaaluasendist sama kaugel kui algasend. Jäänud korraks seisma, hakkab koormis analoogiliselt algasendisse tagasi liikuma. Jõudes tagasi asendisse A, hakkab liikumine korduma: koormis hakkab tasakaaluasendi ümber perioodiliselt edasi-tagasi võnkuma.

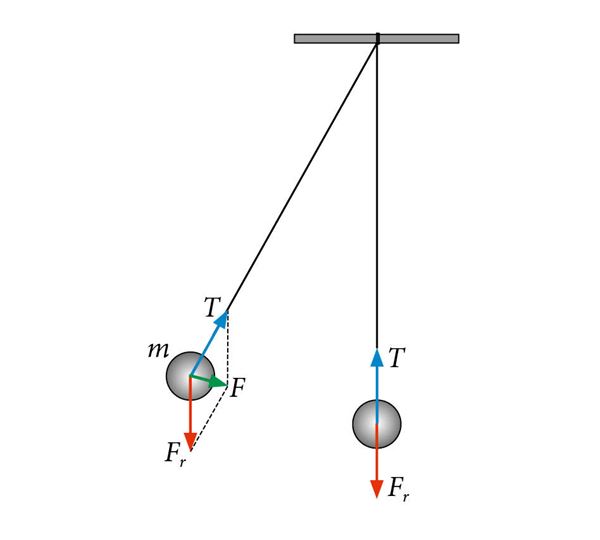
Teame, et keha liikuma panemiseks peame rakendama jõudu. Niitpendlile mõjub kaks jõudu, üks on koormisele mõjuv raskusjõud F_r ja teine niidi tõmbejõud T. Kui pendel ripub vertikaalselt, on raskusjõud ja tõmbejõud tasakaalus (sama suured, kuid vastassuunalised). Kui aga pendel viia tasakaaluasendist välja, siis on raskusjõud ja niidi tõmbejõud erisuunalised ning nad ei tasakaalusta teineteist. Nende resultantjõud F ei ole enam võrdne nulliga, vaid on suunatud tasakaaluasendi poole. See jõud panebki pendli liikuma, tekitades perioodilise edasi-tagasi võnkumise. Sellise liikumise kirjeldamine jõu kaudu on suhteliselt keeruline.

Lihtsam on pendli liikumist analüüsida energia seisukohalt. Juba Galilei arvas, et pendli võnkumiste korral peab olema midagi jäävat, sest võnkumised pidevalt korduvad. Kuna tol ajal energia mõistet ja energia jäävuse seadust ei tuntud, siis jäigi see jääv suurus leidmata.

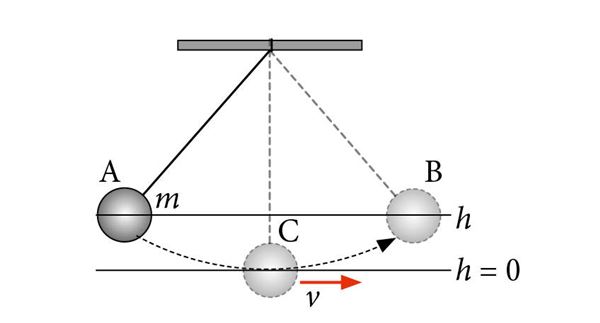
Kui me viime pendli tasakaaluasendist C võnkumiste algasendisse A, siis omandab koormis potentsiaalse energia mgh (koormis tõuseb tasakaaluasendiga võrreldes kõrgusele h). Kui me laseme koormise lahti, hakkab see algasendi suunas tagasi liikuma. Kui niiti ei oleks, kukuks koormis alla, niit sunnib aga koormist liikuma ringi kaart mööda. Potentsiaalse energia kahanedes hakkab suurenema koormise kineetiline energia. Kineetiline energia saavutab maksimumi $\frac{m{v}^2}{2}$, kui koormis on jõudnud tasakaaluasendisse C. Nüüd on potentsiaalne energia võrdne nulliga ja seetõttu on kogu algoleku potentsiaalne energia muundunud kineetiliseks energiaks $mgh=\frac{m{v}^2}{2}$. Tasakaaluasendist liigub koormis inertsi mõjul edasi, kuni jõuab parempoolsesse äärmisse asendisse B. Energia jäävuse tõttu tõuseb ta samale kõrgusele tagasi. Nüüd on kineetiline energia saanud võrdseks nulliga, koormise koguenergia on jälle tema potentsiaalne energia. Asendist B hakkab liikumine korduma, nüüd aga vastupidised suunas. Lõpptulemusena saame perioodiliselt korduva edasi-tagasi võnkumise.

Peamiseks füüsikaliseks suuruseks, mida pendli juures mõõdetakse, on pendli võnkeperiood. Pendli võnkeperiood on aeg, mis on võrdne ühe täisvõnke kestusega. Täisvõnkeks loetakse liikumist liikumise algasendist A teise äärmisse asendisse B ja sealt algasendisse A tagasi. Võnkeperioodi tähis on T.

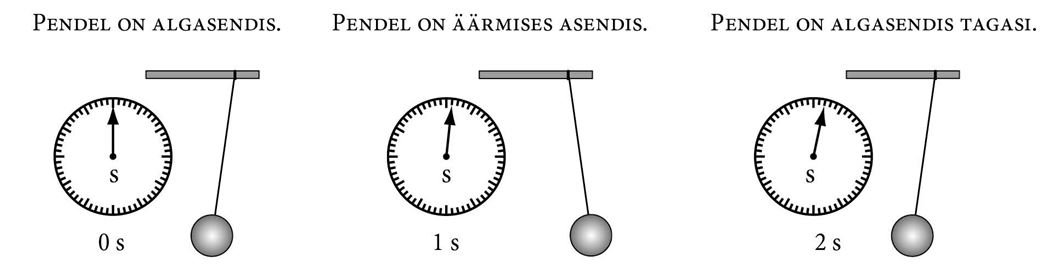
Joonisel toodud näites on pendli võnkeperiood T = 2 s. Mõõtmistäpsuse suurendamiseks määratakse mitme täisvõnke, näiteks 10 täisvõnke kestus (t) ja saadud tulemus jagatakse võngete arvuga (n) ehk kümnega: $T=\frac{t}{n}\text{.}$

Lisaks võnkeperioodile on kasutusel võnkesageduse mõiste, mis näitab mitu võnget sooritab pendel ühes sekundis. Mida suurem on võnkesagedus, seda rohkem võnkeid pendel ühes sekundis sooritab. Võnkesagedus on võrdne võnkeperioodi pöördväärtusega:

$\text{võnkesagedus}=\frac{1}{\text{võnkeperiood sekundites}}\text{.}$

Võnkesageduse tähiseks on f. Seega

Perioodi T mõõtühikuks on ajaühik üks sekund (1 s). Sagedusel on eraldi mõõtühik 1 herts (1 Hz). Sagedus on üks herts (1 Hz) kui võnkuv keha teeb ühe täisvõnke sekundis. Sagedamini kasutatavad kordsed ühikud on: 1 kHz = 10³ Hz; 1 MHz = 10⁶ Hz; 1 GHz = 10⁹ Hz. Sageduse ühikule on antud nimetus saksa füüsiku Heinrich Hertzi auks.

Kui näiteks pendli võnkeperiood on pool sekundit (T = 0,5 s), teeb pendel sekundis kaks võnget, kui aga võnkeperiood on kaks sekundit (T = 2 s), teeb pendel sekundis ainult pool võnget. Esimesel juhul on sagedus f = 2 Hz, teisel juhul f = 0,5 Hz.

Amplituud on võnkuva keha suurim kaugus tasakaaluasendist. Niitpendli korral liigub koormis ringi kaart mööda, seetõttu on amplituud võrdne tasakaaluasendist amplituudasendisse viiva kaare pikkusega s_m. Mida suurem on võnkeamplituud, seda suurem on võnkuva pendli koguenergia.

Kui pendlitega katsetada, siis selgub huvitav tõsiasi: väikeste hälvete korral tasakaalu­asendist ei sõltu periood koormise massist ega võnkeamplituudi suurusest, vaid ainult pendli pikkusest. Pikema pendli võnkeperiood on lühema pendli võnkeperioodist suurem. Seos pendli pikkusega ei ole lineaarne. Nii näiteks on 1 s võnkeperioodiga pendli pikkuseks umbes 25 cm, 2 s võnkeperioodiga pendli pikkuseks umbes 1 m.

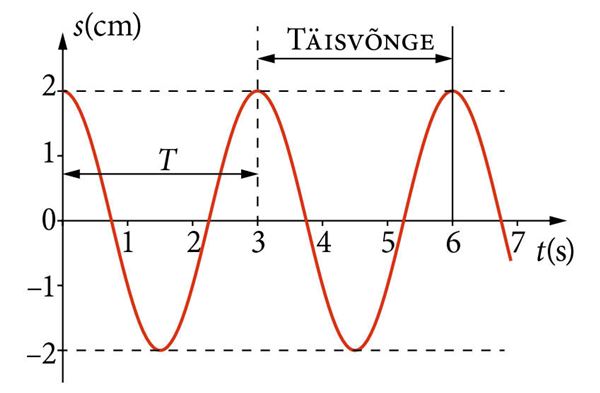
Võnkumisi kujutatakse graafiliselt, kus vertikaalteljele kantakse hälve tasakaaluasendist ja horisontaalteljele aeg. Nii näeks pendli võnkumiste graafik, kui me viime pendli algasendist kaugusele s ja laseme lahti, välja järgmine. Antud võnkumiste periood on 3 s ja võnkumiste amplituud 2 cm.

Lihtsaks pendliks on lisaks niitpendlile vedrupendel. Vedrupendli korral riputatakse koormis vedru otsa. Joonisel on vertikaalne vedrupendel.

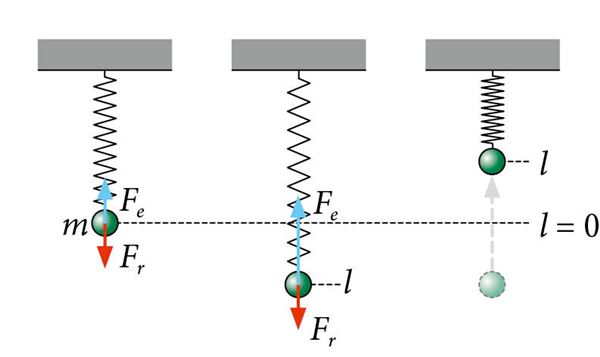
Tõmmates koormise tasakaaluasendist mingi pikkuse l võrra allapoole ja lastes lahti, hakkab see vedru elastsusjõu mõjul perioodiliselt üles-alla võnkuma. Nüüd on liikumapanevaks jõuks vedru elastsusjõud. Liikumisel kehtib energia jäävuse seadus. Väljavenitatud vedru potentsiaalne energia muutub tasakaaluasendisse jõudmisel kineetiliseks energiaks. Koormis liigub inertsi mõjul tasakaaluasendist ülespoole kõrgusele l, kus kogu kineetiline energia on muutunud vedru elastsusjõu potentsiaalseks energiaks. Ülemisest asendist hakkab koormis elastsusjõu mõjul liikuma allapoole ja kogu liikumine hakkab perioodiliselt korduma.

1. Vasta õppetüki alguses olevatele küsimustele.
2. Leia ümbritsevast keskkonnast võnkumisi.
3. Millised lühtri omadused on pendlile üle kantud?
4. Kirjelda niitpendli võnkumisi energia seisukohast.
5. Valmista niidist ja näiteks toavõtmest pendel ning tee mõned lihtsad katsed:
   ​– Vaatle liikumise kordumist võnkumisel.
   ​– Peata pendel ja tee kindlaks tasakaaluasend.
   ​– Vii pendel tasakaaluasendist välja ja lase võnkuma. Tee kindlaks amplituud­asendid.
   ​– Määra võnkeperiood. Arvuta võnkesagedus.
6. Miks saab pendlit kasutada aja mõõtmiseks?
7. Miks on võnkesageduse iseloomustamiseks vaja eraldi ühikut?