*Perioodiline funktsioon

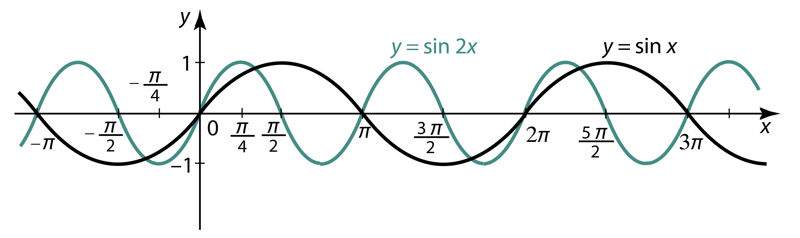
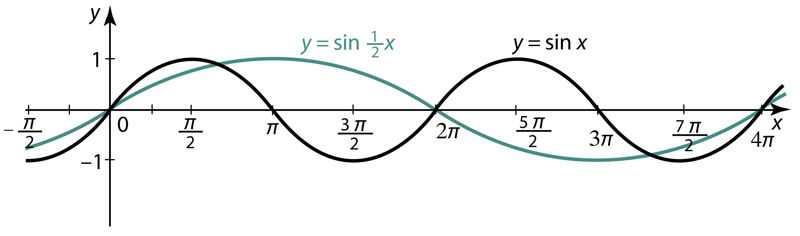Trigonomeetriliste funktsioonide käsitlemisel selgus, et need on perioodilised funktsioonid, kus­juures siinus- ja koosinus­funktsiooni periood on 2π, tangens­funktsiooni periood aga π.

Üldiselt nimetatakse funktsiooni y = f (x) perioodiliseks, kui leidub selline arv p > 0, mille lisamisel argumendi mis tahes väärtusele määramis­piirkonnast funktsiooni väärtus ei muutu, s.t kui argumendi x iga väärtuse korral määramis­piirkonnast

f (x + p) = f (x), x ∈ X.

Funktsiooni perioodiks nimetame edas­pidi vähimat positiivset arvu p, mille korral kehtib viimane seos.

Trigonomeetriliste funktsioonide korral vastavad võrdusele f (x + p) = f (x) võrdused

sin(x + 2π) = sin x,
​cos(x + 2π) = cos x,
​tan(x + π) = tan x.

Näide 1.

Funktsioon f (x) = 3 – 2 sin x on perioodiline, sest leidub positiivne arv p = 2π nii, et f (x + 2π) = f (x):

f (x + 2π) = 3 – 2 sin(x + 2π) = 3 – 2 sin x = f (x).

Näide 2.

Selgitame, kas funktsioon y = cos 0,5x on perioodiline.

Võtame p = 2π ja kontrollime võrduse f (x + p) = f (x) kehtivust:

cos 0,5(x + 2π) = cos (0,5x + π) = –cos 0,5x.

Kuigi tulemus pole cos 0,5x, ei tähenda see veel, et funktsioon y = cos 0,5x ei ole perioodiline. Võib ju arvu p valik olla eba­õnnestunud. Olgu nüüd p = 4π.

Siis

cos 0,5(x + 4π) = cos (0,5x + 2π) = cos 0,5x.

Seega on funktsioon y = cos 0,5x siiski perioodiline.

Kui funktsioon y = f (x) on perioodiline perioodiga p, siis saame funktsiooni graafiku jaotada täpselt ühe­sugusteks perioodi pikkusteks osadeks. See­tõttu on funktsiooni y = f (x) graafik sama­sugune nii piir­kondades

\left[x_0;\ x_0+p\right]; \left[x_0+p;\ x_0+2p\right]; \left[x_0+2p;\ x_0+3p\right]; …,

kuid ka piirkondades

\left[x_0;\ x_0+p\right]; \left[x_0-p;\ x_0\right]; \left[x_0-2p;\ x_0-p\right]; … .

Ühe perioodilise funktsiooni graafik on esitatud joonisel 3.27.

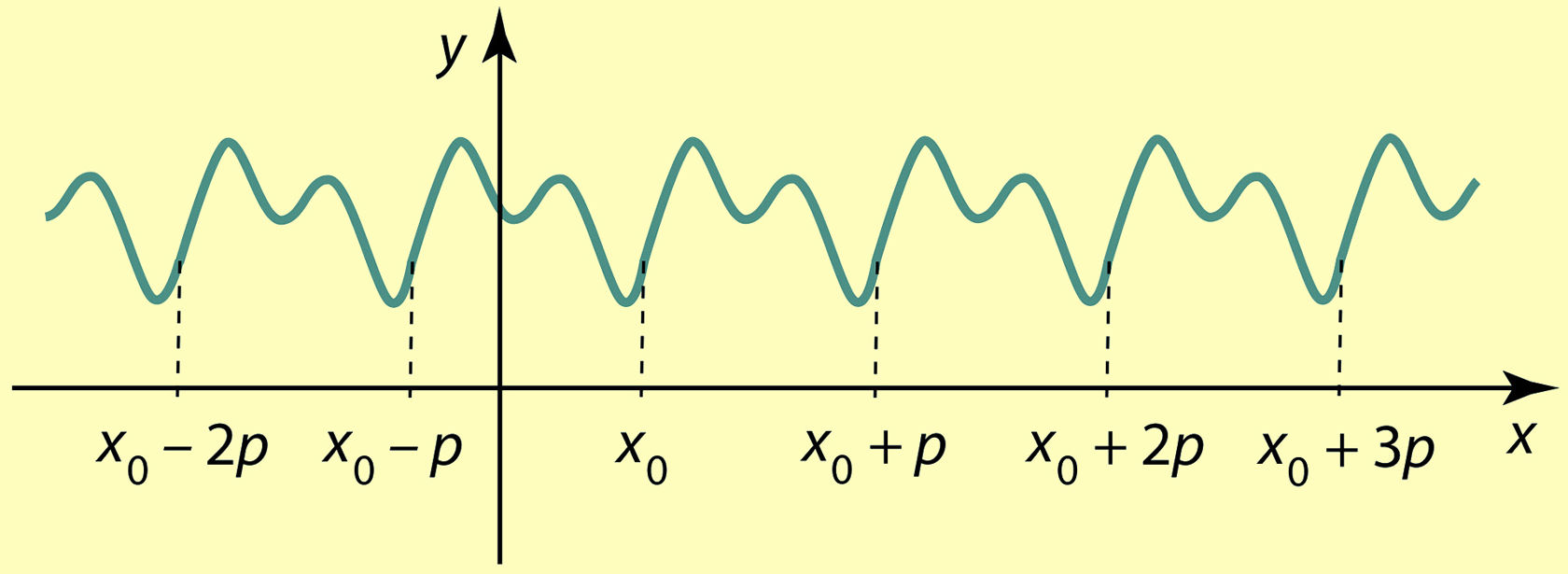Joon. 3.27

Nagu teame, on funktioonid y = sin x, y = cos x, y = tan x perioodilised. Kuid ka funktsioonid y = sin kx, y = cos kx, y = tan kx osutuvad perioodilisteks. Nende perioodid on vastavalt p=\frac{2\pi}{k}, p=\frac{2\pi}{k} ja p=\frac{\pi}{k}. Kaks vastavat näidet on joonistel 3.28 ja 3.29.

More like this
More options

Ülesanded B

Ülesanne 723. Perioodiline funktsioon

y=\sin x+\cos x
f ( x + ) =  = 

y=4+2\cos x
f (x + ) =  = 

y=2+\tan x
f (x + ) =  = 

y=\sin x+\tan x
f (x + ) =  = 

y=\sin2x
f (x + ) =  = 

y=\tan\frac{3}{4}x
f (x + ) =  = 

y=\cos\left(x+2\right)
f (x + ) =  = 

y=\tan4x
f (x + ) =  = 

y=\sin0,5x-\cos x
f (x + ) =  = 

Ülesanne 724. Funktsiooni uurimine
Joon. 3.28

Vastus. X_0 = ; X^+ = ; X^- = ; X\uparrow = ; X\downarrow = ; maksimum­punktid on ; miinimum­punktid on ; n ∈ Z.

Joon. 3.29

Vastus. X_0 = ; X^+ = ; X^- = ; X\uparrow = ; X\downarrow = ; maksimum­punktid on ; miinimum­punktid on ; n ∈ Z.

More like this
More options