Nagu teame, on arv r arvu N logaritm alusel a, mida kirjutatakse lühemalt r = logaN, kui ar = N, kus a > 0 ja a ≠ 1. Kui nüüd arv N saab kõikvõimalikke positiivseid reaalarvulisi väärtusi, seab võrdus r = logaN igale reaalarvule N piirkonnast (0; ∞) vastavusse ühe arvu r ∈ R. Seega defineerib võrdus r = logaN funktsiooni, mida nimetatakse logaritmfunktsiooniks. Tähistades nagu ikka argumendi tähega x ja funktsiooni tähega y, saame logaritmfunktsiooni traditsioonilise esitusviisi y = loga x.
Selgub, et logaritmfunktsioon on eksponentfunktsiooni y = ax, kus a > 0 ja a ≠ 1, pöördfunktsioon. Eksponentfunktsioon on pidev ja kogu oma määramispiirkonnas kas kasvav (a > 0 korral) või kahanev (0 < a < 1 korral). Järelikult on eksponentfunktsioonil olemas pöördfunktsioon (peatükk 2.16). Pöördfunktsiooni leidmiseks avaldame eksponentfunktsiooni y = ax argumendi x muutuja y kaudu: x = loga y. Nüüd loeme endise argumendi x funktsiooniks ja muutuja y argumendiks ning läheme üle traditsioonilistele tähistele. Tulemusena saame funktsiooni y = ax pöördfunktsiooni y = loga x, mis ongi logaritmfunktsioon. Nagu eksponentfunktsiooni korral, nii ka nüüd on a > 0 ja a ≠ 1. Niisiis kokkuvõtvalt:
logaritmfunktsiooniks nimetatakse funktsiooni y = loga x, kus a > 0, a ≠ 1.
Logaritmfunktsioon on eksponentfunktsiooni y = ax, a > 0, a ≠ 1 pöördfunktsioon.
Näiteks funktsiooni y = 3x pöördfunktsioon on y = log3 x.
Et logaritmfunktsioon on eksponentfunktsiooni pöördfunktsioon, siis on tema määramispiirkonnaks eksponentfunktsiooni muutumispiirkond ja muutumispiirkonnaks eksponentfunktsiooni määramispiirkond. Järelikult on logaritmfunktsiooni y = loga x määramispiirkonnaks vahemik 0 < x < ∞, muutumispiirkonnaks aga kogu reaalarvude hulk R.
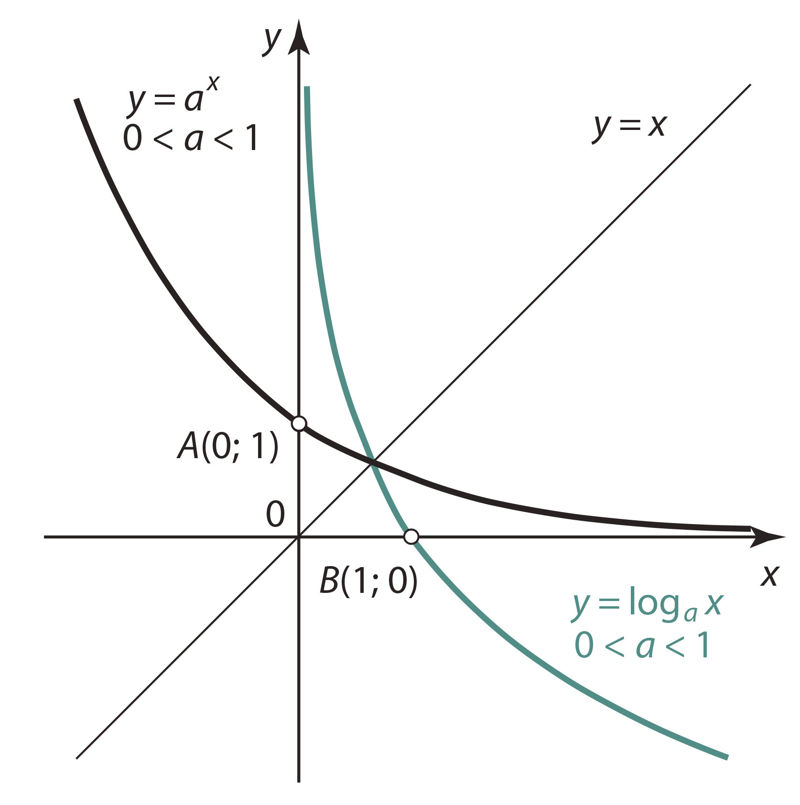
Logaritmfunktsiooni graafiku saame vastava eksponentfunktsiooni graafiku peegeldamisel sirgest y = x, mis tähendab, et funktsioonide y = loga x ja y = ax graafikud on sümmeetrilised sirge y = x suhtes (joonis 3.15 ja 3.16).
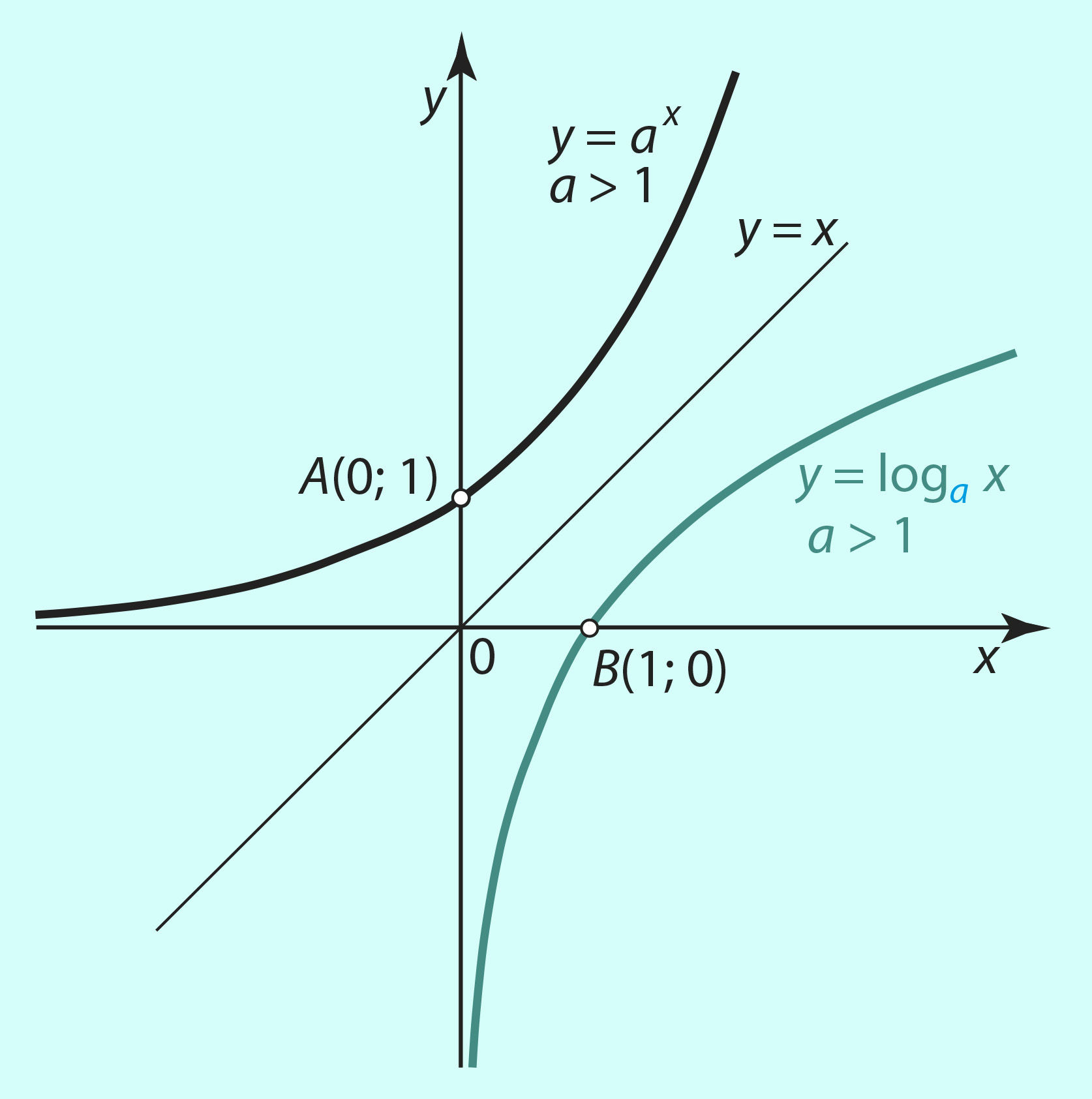 Joon. 3.15 | ||||||
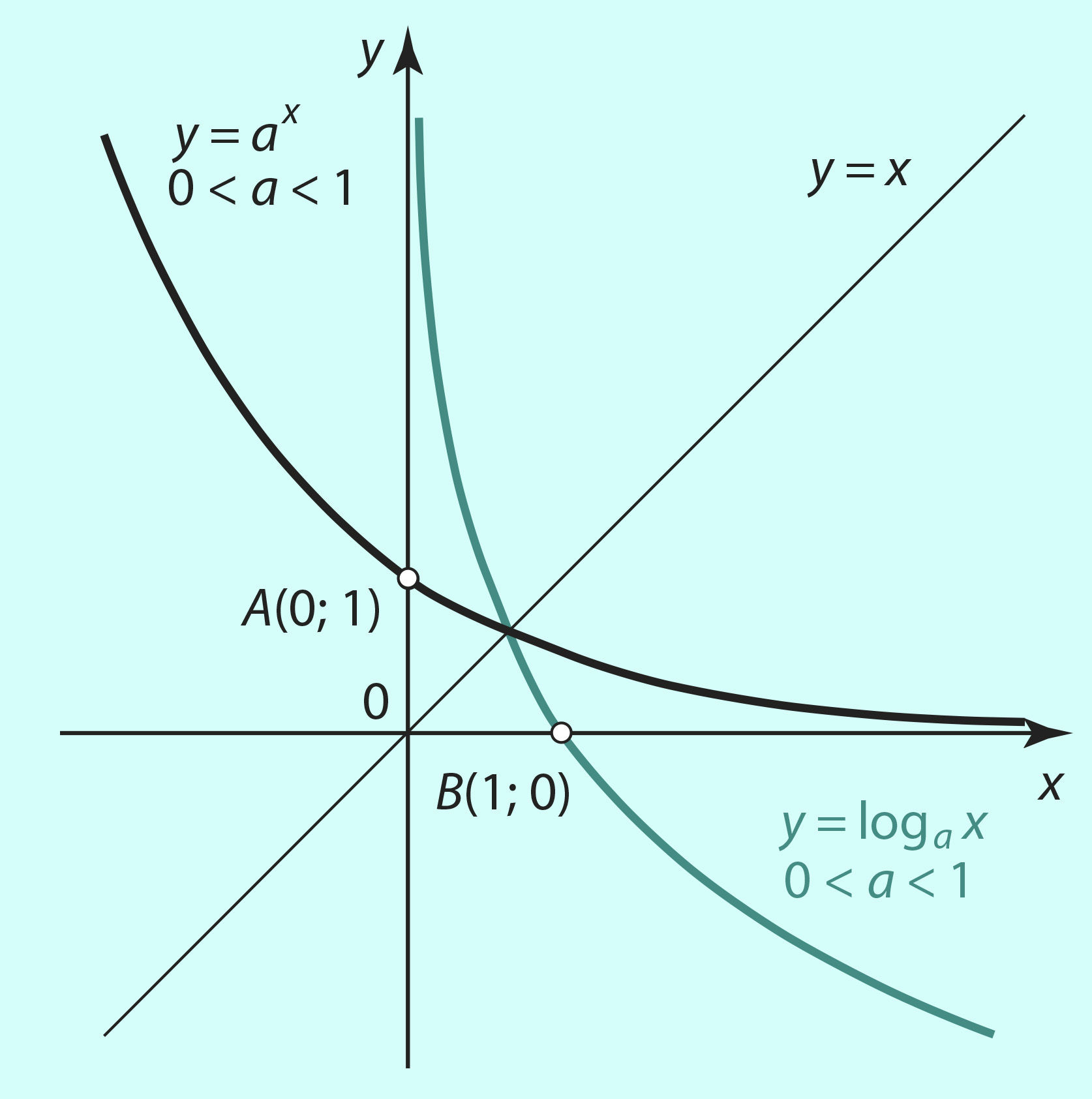 Joon. 3.16 | ||||||
Logaritmfunktsiooni definitsioonist ja graafikult, mis on pidev joon, loeme välja logaritmfunktsiooni omadused.
- Kui a > 1 (joonis 3.15).
- Nullkohti on üks, x0 = 1. Graafik läbib punkti B(1; 0).
- Graafik läbib punkti (a; 1).
- Positiivsuspiirkonnaks on vahemik 1 < x < ∞. Negatiivsuspiirkonnaks on vahemik 0 < x < 1.
- Funktsioon on kasvav kogu määramispiirkonnas, s.t vahemikus 0 < x < ∞.
- Argumendi x väärtuste tõkestamatul kasvamisel kasvavad loga x väärtused tõkestamatult. Kui argumendi väärtused lähenevad tõkestamatult nullile, vähenevad loga x väärtused tõkestamatult.
- Funktsiooni graafiku asümptoodiks on y-telg.
- Kui 0 < a < 1 (joonis 3.16).
- Nullkoht on sama, mis juhul a > 1, s.o x0 = 1. Graafik läbib punkti B(1; 0).
- Graafik läbib punkti (a; 1).
- Positiivsuspiirkonnaks on vahemik 0 < x < 1. Negatiivsuspiirkonnaks on vahemik 1 < x < ∞.
- Funktsioon on kahanev kogu määramispiirkonnas, s.t vahemikus 0 < x < ∞.
- Argumendi x väärtuste tõkestamatul kasvamisel vähenevad loga x väärtused tõkestamatult. Kui argumendi väärtused lähenevad tõkestamatult nullile, kasvavad loga x väärtused tõkestamatult.
- Funktsiooni graafiku asümptoodiks on y-telg.
Logaritmfunktsioonide y = log x ja y = ln x graafikud on joonisel 3.17. Sellelt on ka näha, kuidas mõjub logaritmfunktsiooni graafikule aluse kasvamine.
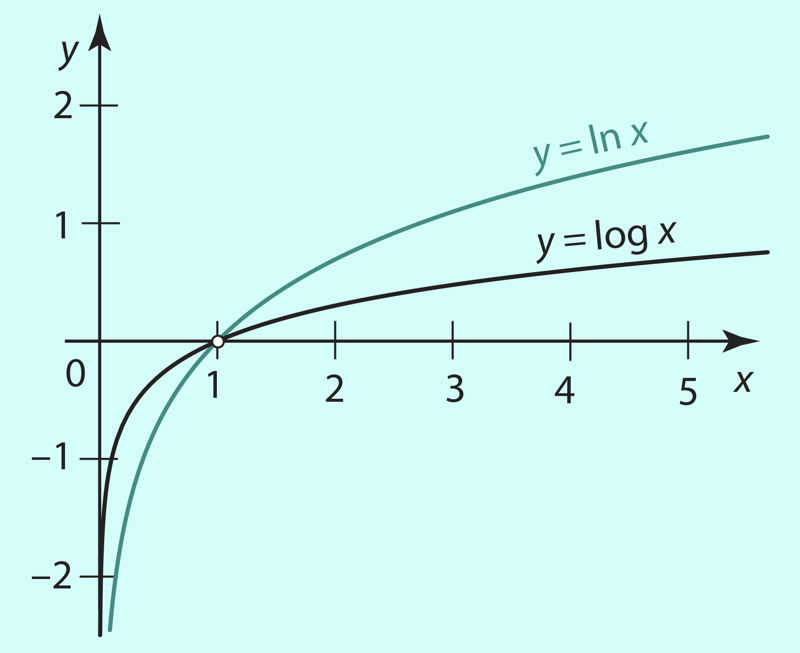
Joon. 3.17 | ||||||
Näide 1.
Selgitame, kas 1) log5 0,6; 2) log0,8 9; 3) ln 2 on positiivne või negatiivne.
Tugineme logaritmfunktsiooni kolmandale omadusele või veelgi parem, kujutame ette vastava funktsiooni graafikut:
- log5 0,6 < 0, sest a = 5 > 1 tõttu kuulub argumendi väärtus 0,6 funktsiooni y = log5 x negatiivsuspiirkonda;
- log0,8 9 < 0, sest a = 0,8 < 1 tõttu kuulub argumendi väärtus 9 funktsiooni y = log0,8 x negatiivsuspiirkonda;
- ln 2 > 0, sest argumendi väärtus 2 kuulub funktsiooni y = ln x positiivsuspiirkonda (joonis 3.17).
Näide 2.
Selgitame, kumb on suurem, kas 1) log 2 või log 6; 2) log0,2 3 või log0,2 0,7.
- Et funktsioon y = log x on kasvav, siis vastab suuremale argumendi väärtusele suurem funktsiooni väärtus. Seega log 2 < log 6.
- Et funktsioon y = log0,2 x on kahanev, siis vastab suuremale argumendi väärtusele väiksem funktsiooni väärtus. Seega log0,2 3 < log0,2 0,7.
Näiteülesande 2 lahendamisel esinenud mõttekäigud saab kokkuvõtlikult sõnastada järgmise teoreemina:
kui 0 < a < 1, siis loga x1 > loga x2 ⇔ x1 < x2;
kui a > 1, siis loga x1 < loga x2 ⇔ x1 < x2.
Näide 3.
Lahendame võrratuse log0,4 (2x – 4) < 0.
Selle võrratuse lahendamine tähendab funktsiooni y = log0,4 (2x – 4) negatiivsuspiirkonna leidmist. Et a = 0,4 < 1, siis on funktsiooni väärtused negatiivsed, kui logaritmitav on suurem ühest. Niisiis, 2x – 4 > 1 ehk x > 2,5.
Näide 4.
Lahendame võrratuse log (1 – x) < 2.
Kirjutame antud võrratuse kujul log (1 – x) < log 100. Et a = 10 > 1 korral vastab suuremale argumendi väärtusele suurem funktsiooni väärtus, siis 1 – x < 100, millest x > –99. Seejuures peab logaritmitav olema alati positiivne, s.t 1 – x > 0, millest x < 1. Järelikult on antud võrratuse lahendiks vahemik –99 < x < 1.
Näide 5.
Leiame funktsiooni y = log (x2 – x3) määramispiirkonna, s.t argumendi x väärtuste hulga, mille korral funktsiooni väärtusi saab arvutada.
Logaritmitav peab olema alati positiivne, seega
x2 – x3 > 0 ehk x2 (1 – x) > 0.
Et x ≠ 0 (nullist ei saa logaritmi leida), siis x2 > 0 ja 1 – x > 0, millest x < 1. Tingimuse x ≠ 0 tõttu koosneb määramispiirkond kahest vahemikust:
x < 0, 0 < x <1.
Logaritmfunktsiooni abil kirjeldatakse ka mitmeid nähtusi.
Näide 6.
Kui kahe heli tugevused on I ja I0, siis nende tugevuste erinevust L mõõdetakse detsibellides (dB) ja arvutatakse valemiga
- mitmekordselt ületab tegelikult heli tugevusega I inimese kuulmislävele vastava helitugevuse I0, kui inimene kuuleb heli I helitugevusega L = 1 dB;
- millisena kuuleb heli inimene, kui heli tegelik tugevus I = 126 · I0?
- Et L = 1 dB, siis
1=10\cdot\log\frac{I}{I_0} , millest\log\frac{I}{I_0}=0,1 jaI\approx1,26\cdot I_0 . - Ülesande tingimuste kohaselt
L=10\cdot\log\frac{126I_0}{I_0} =10\cdot\log126 ≈ 21.
Võrreldes omavahel neid kahte juhtu, selgub, et kui heli tegelik tugevus I suurenes 100 korda (1,26I0 ja 126I0), tajus inimene helitugevuse suurenemist vaid 21 korda (1 dB ja 21 dB).
Ülesanded A
Ülesanne 662. Pöördfunktsiooni leidmine
Ülesanne 663. Logaritmfunktsioon
Milline on nende funktsioonide korral määramispiirkond, nullkohad, positiivsus- ja negatiivsuspiirkond, kasvamis- ja kahanemisvahemik ning millised on ekstreemumkohad?
Ülesanne 664. Logaritmfunktsioon
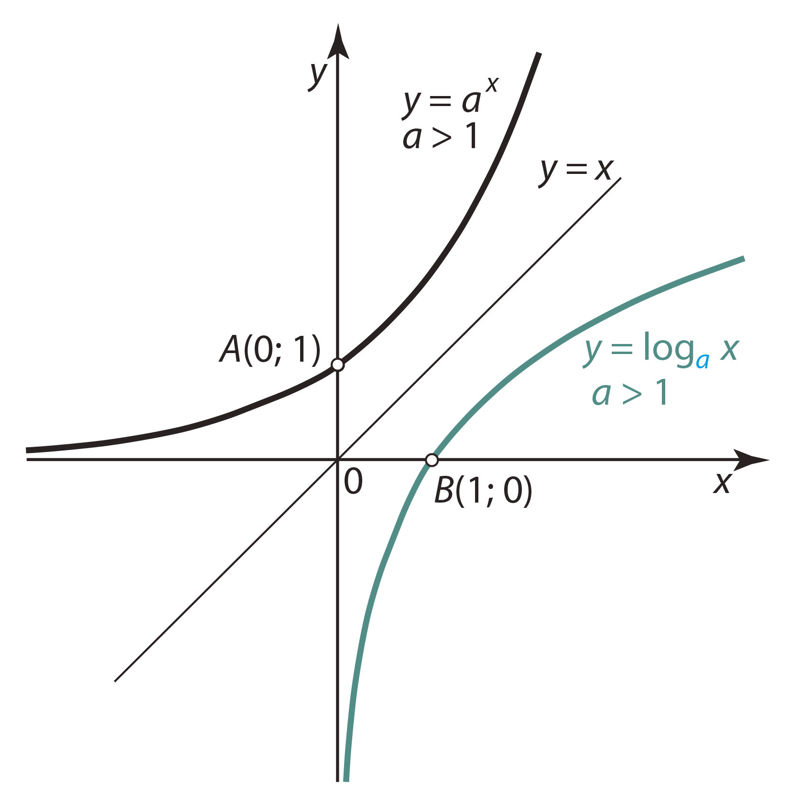
Vastus. Joonisel 3.15 oleva logaritmfunktsiooni korral a = ja joonisel 3.16 oleva logaritmfunktsiooni korral a = .
Ülesanne 665. Logaritmfunktsioon
Arvestades, et funktsioonide
Milline on nende funktsioonide korral määramispiirkond, nullkohad, positiivsus- ja negatiivsuspiirkond, kasvamis- ja kahanemisvahemik ning millised on ekstreemumkohad?
Vastus. Mõlema korral:
Ülesanne 666. Logaritmfunktsioon
Vastus.
Ülesanne 667. Logaritmfunktsioon
Ülesanne 668. Logaritmi väärtus
Ülesanne 669. Logaritmi väärtus
Ülesanne 670. Funktsiooni määramispiirkond
Ülesanne 671. Helitugevus
Kui kahe heli tugevused on I ja I0, siis nende tugevuste erinevust L mõõdetakse detsibellides (dB) ja arvutatakse valemiga
Kasutades seda valemit, leidke,
- mitme detsibelline on helitugevus siis, kui
- I = I0,
Vastus. Helitugevus on siis dB. - I =1000 I0, s.t mängib vaikne rahulik muusika?
Vastus. Helitugevus on siis dB.
- I = I0,
- mitmekordselt ületab tegeliku heli tugevus I kuulmisläve I0, kui
- toimub vestlus (L = 65 dB),
Vastus. Tegeliku heli tugevus ületab kuulmislävekorda. - on äike (L = 110 dB)?
Vastus. Tegeliku heli tugevus ületab kuulmislävekorda.
- toimub vestlus (L = 65 dB),
Ülesanded B
Ülesanne 672. Tõestamine
Tõestage, et funktsioonide
Ülesanne 673. Logaritmi väärtus
Kui
Kui
kui
kui
Ülesanne 674. Logaritmi väärtus
Ülesanne 675. Funktsiooni määramispiirkond
Antud funktsioon | Määramispiirkond |
