Järgnevas vaatleme kahte näidet sellest, kuidas piirprotsessi kasutades saab leida kõverjoone pikkuse ja kõveraga piiratud kujundi pindala. Olgu selleks kõverjooneks ringjoon. Põhikoolist teame, et ringjoone pikkus C ja ringi pindala S arvutatakse järgmiselt:
C = 2πr ja S = πr2.
Tõestame need valemid.
Ringjoone pikkus piirväärtusena
Ringjoone pikkust ei ole otseselt võimalik mõõta mingi pikkusühiku abil, sest pikkusühikud (1 cm, 1 m jne) on kujutatavad sirglõikudena, kuid ringjoon on kõverjoon. Samas tunnetame me intuitiivselt, et ringjoonel on pikkus olemas. Näiteks kui ringikujuliselt asetatud nööri tõmbame sirgeks, siis saadud lõigu pikkus on ühtlasi ka ringjoone pikkus.
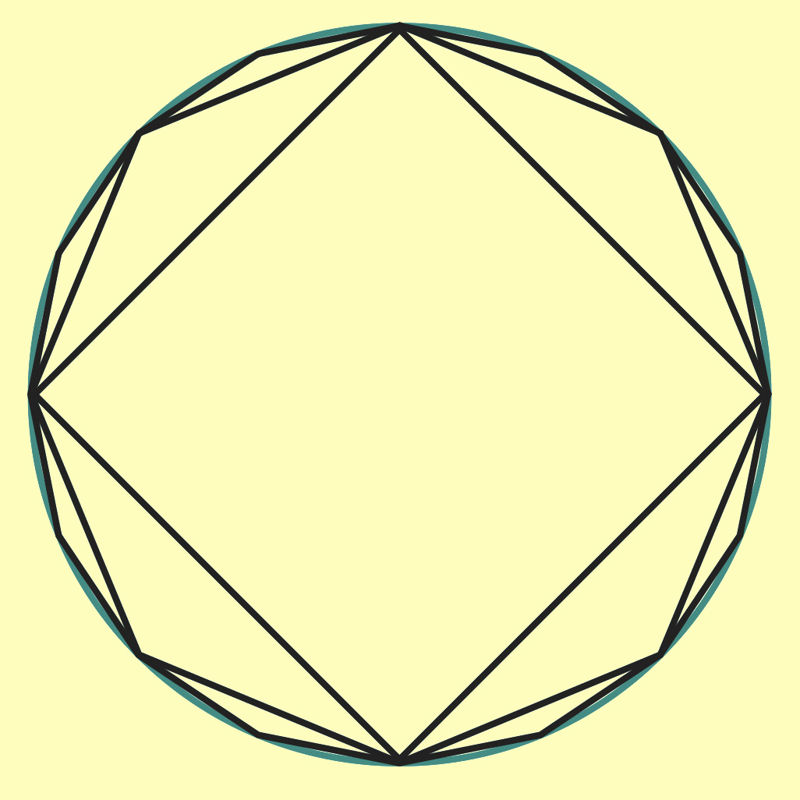
Joon. 2.12
|
||||||
Ringjoone pikkuse arvutamise täpse valemi leidmiseks moodustame kumera hulknurga, mille ümbermõõt on ligikaudu võrdne ringjoone pikkusega. Selleks joonestame ringi sisse kõigepealt näiteks korrapärase nelinurga ehk ruudu (joonis 2.12). Kahekordistades hulknurga tippude arvu, saame korrapärase kaheksanurga, mille ümbermõõt erineb ringjoone ümbermõõdust vähem kui nelinurga ümbermõõt. Jätkates kahekordistamise protsessi, saame hulknurgad, mille ümbermõõdud lähenevad üha enam ringjoone pikkusele. Seetõttu võime ringjoone pikkuse defineerida järgmiselt:
ringjoone pikkuseks nimetatakse korrapäraste kõõlhulknurkade ümbermõõtude jada piirväärtust hulknurga tippude arvu tõkestamatul kasvamisel.
Oletame, et meil on ringi raadiusega r joonestatud korrapärane n-nurk (joonis 2.13) küljepikkusega an. Ühendades hulknurga tipud ringi keskpunktiga O, jaotub kõõlhulknurk n võrdhaarseks kolmnurgaks. Iga sellise kolmnurga tipunurk on
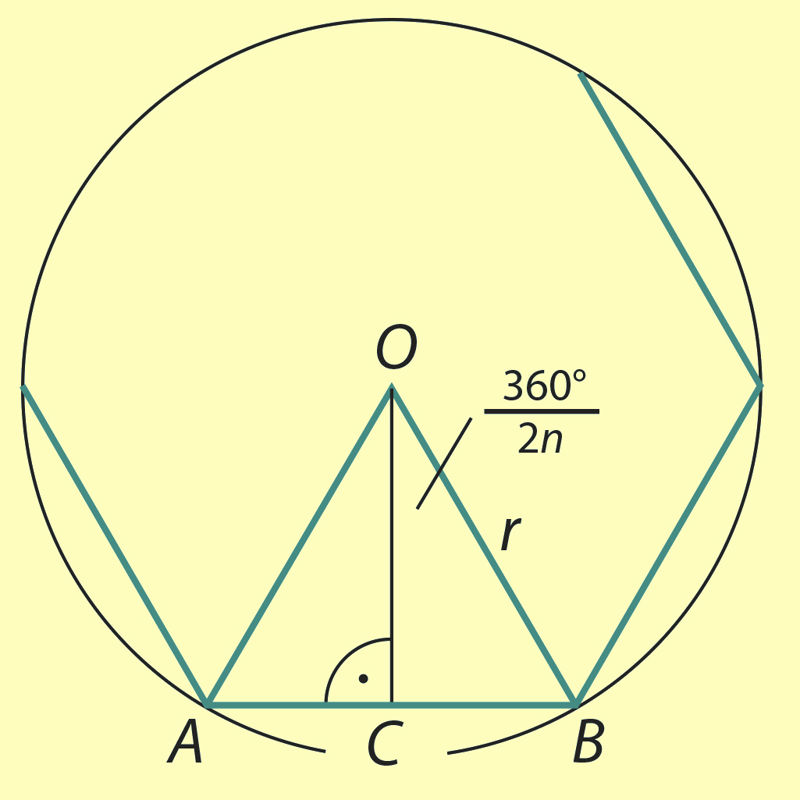
Joon. 2.13 |
||||||
Vaatleme ühte nendest kolmnurkadest, näiteks kolmnurka OAB. Tõmbame selle kolmnurga alusele AB kõrguse OC. Teame, et see kõrgus poolitab kolmnurga aluse ja tipunurga. Täisnurksest kolmnurgast OBC saame:
Et selliseid kolmnurki on n tükki, on kõõlhulknurga ümbermõõt
Definitsiooni kohaselt avaldub ringjoone pikkus siis piirväärtusena:
=
Et ringjoone pikkus on lõplik arv, peab ka
Veenduge, et
Arvestades, et
C = 2πr.
Ringi pindala piirväärtusena
Ka ringi pindala ei ole otseselt võimalik mõõta meile tuntud pindalaühikutega (ühikruutudega pindalaga 1 cm2, 1 m2 jne). Seetõttu toimime analoogiliselt eelmises punktis tehtuga: kujundame ringi sisse korrapärase kõõlhulknurga ja lähendame selle pindala ringi pindalaga.
Ringi pindalaks nimetatakse ringi sisse kujundatud korrapäraste kõõlhulknurkade pindalade jada piirväärtust hulknurga tippude arvu tõkestamatul kasvamisel.
Ringi pindala valemi tuletamiseks kasutame taas joonist 2.13. Kolmnurga AOB pindala
Ringi pindala S avaldub seega järgmiselt:
Et
S = πr2.
Ülesanded B
Ülesanne 387. Rõnga pindala
Vastus. S =
Ülesanne 388. Ruudu sise- ja ümberringjoon
Ülesanne 389. Korrapärase kõõlkolmnurga pindala
Vastus. S =
Ülesanne 390. Korrapärase puutujakolmnurga pindala
Vastus. S =
Ülesanne 391. Korrapärase kuusnurga ümberringjoone ja siseringjoone pikkuste suhe
- 2 cm.
Vastus. See suhe on. - a cm.
Vastus. See suhe on.
Ülesanne 392. Korrapärase n-nurga pindalade suhe
Vastus. Nende n-nurkade pindalad suhtuvad nagu
Ülesanne 393. Ringi sisse kujundatud hulknurk
- korrapärane nelinurk?
Vastus.% - korrapärane kuusnurk?
Vastus.% - korrapärane 12-nurk?
Vastus.%
Ülesanne 394. Varjutatud osa pindala
Ülesanne 395. Varjutatud osa pindala
Ülesanne 396. Täisnurkse kolmnurga siseringjoone raadius
Vastus. r =
Ülesanne 397. Ringi pindala valem
Ülesanne 398. Ringjoone pikkuse valem
Ülesanne 399. Hulknurkade pindalade summa piirväärtus
Vastus. Selles protsessis tekkivate hulknurkade pindalade summa piirväärtus on dm2.